Econometría (II / Práctica)
Tema 4: Variable Dependiente Limitada ( Limited Dependent Variables )
Introducción
En algunos casos, la variable dependiente de interés \(y\) presenta restricciones en los valores que puede asumir. Esto es conocido como Variable Dependiente Limitada (Limited Dependent Variable - LDV, en inglés). Algunos ejemplos comunes incluyen:
Participación laboral: Basados en un modelo de oferta laboral, nos interesa estudiar la decisión de participar en el mercado laboral:
\[ \begin{array}{ccl} Y = 1 & , & \text{si participa en el mercado laboral} \\ Y = 0 & , & \text{si no participa en el mercado laboral} \end{array} \]
Inversión en investigación y desarrollo (I+D): Al estudiar las limitaciones de inversión en I+D, puede surgir una selección endógena si la muestra está compuesta solo de empresas que ya invierten en I+D.
Introducción (cont.)
Para una respuesta cualitativa (como la respuesta binaria de participación laboral), una primera aproximación puede ser el modelo de Mínimos Cuadrados Ordinarios (OLS):
En algunos casos, OLS puede proporcionar una aproximación aceptable de \(\mathbb{E}(Y|X)\) bajo ciertos supuestos. Sin embargo, tiene limitaciones importantes, tales como:
- Predicciones fuera del rango \([0,1]\): Esto es poco realista, ya que una probabilidad no puede exceder estos límites.
- Efectos marginales constantes: En OLS, el efecto de una variable independiente es constante, lo cual puede ser inadecuado en modelos de respuesta limitada.
Nota: Aquí, “limitaciones” se pone entre comillas ya que discutiremos estos puntos en mayor profundidad.
Outline de los Modelos de LDV
En esta sección, exploraremos los modelos más comunes para variables dependientes limitadas, incluyendo:
- Probit y Logit: Modelos para respuestas binarias.
- Logit/Probit Multinomial, Condicional y Anidado: Modelos para múltiples opciones.
- Poisson: Modelo para variables de conteo.
- Tobit: Modelo para variables censuradas.
- Heckman: Modelo para corrección de sesgo de selección.
- Modelos de Duración: Para analizar el tiempo hasta la ocurrencia de un evento.
Variable dependiente binaria:
LPM, Logit, Probit.
Variable dependiente binaria
Supongamos que la variable dependiente observada toma valores binarios, como los siguientes:
\[ \begin{array}{ccl} Y = 1 & & \text{Si se cumple cierta condición} \\ Y = 0 & & \text{Si no se cumple cierta condición} \\ \end{array} \]
Ejemplo: Participación en el mercado laboral
- \(Y = 1\) si la persona participa en el mercado laboral.
- \(Y = 0\) si la persona no participa.
La media condicional de la población se puede interpretar como la probabilidad de que \(Y = 1\) dado \(X\), es decir, \(\mathbb{E}(Y|X) = P(Y = 1|X)\).
Variable dependiente binaria
Modelo de Probabilidad Lineal ( LPM )
En el modelo de probabilidad lineal, la probabilidad está dada por:
\[ p = \mathbb{E}(Y|X) = X\beta \]
Este modelo se ajusta utilizando Mínimos Cuadrados Ordinarios (OLS):
\[ Y = X\beta + u \]
Variable dependiente binaria: LPM
Potenciales Desventajas de usar LPM (basadas en el texto de pregrado)
- Predicciones fuera del intervalo \([0,1]\):
- No hay garantía de que \(\hat{\beta}_0 + \hat{\beta}_1 x_i\) esté en el rango \([0,1]\).
- Heteroscedasticidad:
- La varianza de \(Y\) en un ensayo Bernoulli está dada por \(p(1-p) = X\beta(\iota_N - X\beta)\).
- Esto implica que la varianza cambia con \(X\) (no es constante).
- Corrección de Heteroscedasticidad:
- Si conocemos la forma de la heteroscedasticidad, podemos corregirla mediante un ajuste por Mínimos Cuadrados Generalizados (GLS).
Variable dependiente binaria: LPM
Ventajas de usar LPM (Angrist y Pischke)
- El LPM es fácil de entender e interpretar, especialmente para evaluar la dirección del efecto de los regresores.
- Menos Supuestos: Se evita hacer supuestos fuertes sobre la forma de la distribución de los errores.
- Robustez a la Heterocedasticidad: El LPM permite correcciones sencillas para la heterocedasticidad mediante el uso de errores estándar robustos.
- Efectos de Tratamiento Heterogéneos: El LPM facilita la estimación de efectos de tratamiento heterogéneos, permitiendo interacciones entre variables explicativas.
- Evita Complejidad Innecesaria: Angrist y Pischke argumentan en Mostly Harmless Econometrics que logit y probit no siempre aportan valor adicional en aplicaciones prácticas, particularmente cuando el interés está en el signo y la magnitud relativa de los coeficientes.
- Aplicable para Identificación Causal: En estudios donde se busca identificar un efecto causal y las probabilidades están en el rango medio, el LPM puede ofrecer resultados robustos y fáciles de interpretar. En estos contextos, ajustar predicciones fuera del intervalo \([0,1]\) puede no ser crítico.
- Comparación Empírica: Estudios empíricos han mostrado que en muchas aplicaciones los coeficientes de LPM, logit y probit son similares en magnitud y signo, especialmente para probabilidades entre 0,1 y 0,9.
Nota: Angrist sugiere que en investigaciones aplicadas, enfocadas en el efecto promedio de tratamiento o en la dirección del efecto, el LPM es una opción práctica y defendible.
Variable Dependiente Binaria:
Modelos Probit y Logit
Objetivo: Modelar la probabilidad \(p\) (media condicional) dentro del intervalo [0,1] usando funciones de distribución de probabilidad.
- Modelo Probit:
- Usa la función de distribución acumulada de la normal estándar. La probabilidad \(p\) está dada por \(p = \mathbb{E}(Y|X) = \Phi(X\beta)\), en donde la función de distribución normal es: \[ \Phi(X\beta) = \int_{-\infty}^{X_i'\beta} \frac{1}{\sqrt{2\pi}} e^{-t^2/2} \, dt \]
- Modelo Logit:
- Usa la función logística para la probabilidad. La probabilidad \(p\) está dada por: \[ p = \mathbb{E}(Y|X) = \Lambda(X\beta) = \frac{1}{1 + e^{-X\beta}} \]
Variable dependiente binaria: Probit y Logit
Se pueden derivar los modelos a partir de una variable latente \(Y^*\), que representa una variable no observada
( podemos pensar en esta variable latente como una variable con ‘mayor libertad’, en el sentido que puede ser no negativa y/o continua “no limitada” ).Ejemplo: En el caso de participación laboral (\(Y\) = 1 si participa, \(Y\) = 0 si no participa), supongamos que hay una variable latente que representa el deseo o la intención de participar:
\[ Y^* = X\beta + u \]
Se observa \(Y\) de la siguiente forma: \[Y=\mathbb{I}\{Y^*>0\}\]
Probabilidad. Por ejemplo, bajo el supuesto de que \(u \sim \mathbb{N}(0,1)\), tenemos: \[ p = \mathbb{E}(Y|X) = P(Y = 1|X) = P(Y^* > 0 |X) = P(u < X\beta) = \Phi(X\beta) \]
Variable dependiente binaria: Probit y Logit
Estimación
- Método de Mínimos Cuadrados No Lineales (NLS):
Una primer pregunta sería si aún podríamos usar la aproximación de OLS (minimizar residuos al cuadrados) para obtener los parámetros estimados, y la respuesta sería, en principio, sí:
\[min_\beta\,(Y-\mathbb{E}(Y|X))'(Y-\mathbb{E}(Y|X))\]
es decir, sería mínimos cuadrados no lineales (NLS).
Aunque teóricamente es posible minimizar el residuo al cuadrado, este enfoque no es eficiente en términos de varianza (ya no es BLUE) ni computacionalmente óptimo.
Variable dependiente binaria: Probit y Logit
Estimación
- Máxima Verosimilitud (MLE):
- Considerando que \(Y\) es un ensayo Bernoulli con probabilidad \(p\), la función de probabilidad para una observación \(i\) es: \[ p_i^{Y_i}(1 - p_i)^{1 - Y_i} \]
- En el caso del probit, \(p_i = \Phi(X_i'\beta)\) y en el caso del logit, \(p_i = \Lambda(X_i'\beta)\).
- El vector de parámetros se estima maximizando la función de log-verosimilitud: \[ \hat{\beta} = \text{arg max}_\beta \sum_{i=1}^n \left( Y_i \cdot \ln(p_i) + (1 - Y_i) \cdot \ln(1 - p_i) \right) \]
Variable dependiente binaria: Probit y Logit
Condiciones de Primer Orden para MLE
- Las condiciones de primer orden para maximizar la log-verosimilitud son: \[ \frac{\partial \ell}{\partial \beta} = \sum_{i=1}^n \left( \frac{Y_i - F_i}{F_i (1 - F_i)} f_i X_i' \right) \]
- Al definir \(w_i = f_i / (F_i (1 - F_i))\), estas condiciones se pueden interpretar como un problema de Mínimos Cuadrados Ponderados No Lineales (NWLS).
Variable dependiente binaria: Probit y Logit
Condiciones de Primer Orden para MLE - Relación Empírica entre LPM, Logit y Probit
- Para valores de probabilidad entre 0.1 y 0.9, se observa una relación aproximada entre los coeficientes de LPM, logit y probit (Amemiya, 1981):
- \(\beta_{\text{Logit}} \approx 4 \beta_{\text{OLS}}\)
- \(\beta_{\text{Probit}} \approx 2.5 \beta_{\text{OLS}}\)
- \(\beta_{\text{Logit}} \approx 1.6 \beta_{\text{Probit}}\)
Variable dependiente binaria: Probit y Logit
Condiciones de Segundo Orden para MLE
Las condiciones de segundo orden para la matriz de varianza de los estimadores son:
Logit: \[ \frac{\partial^2 \ell}{\partial \beta \partial \beta'} = -\sum \Lambda_i (1 - \Lambda_i) X_i X_i' \]
Probit: \[ \frac{\partial^2 \ell}{\partial \beta \partial \beta'} = -\sum \psi_i (\psi_i - X_i' \beta) X_i X_i' \] donde \(\psi_i = \frac{\phi_i}{\Phi_i}\) si \(Y_i = 1\), y \(\psi_i = -\frac{\phi_i}{1 - \Phi_i}\) si \(Y_i = 0\).
Variable dependiente binaria: Probit y Logit
Efectos Marginales
En logit/probit, los coeficientes estimados no representan efectos marginales.
El efecto marginal de un cambio en una variable \(X^{(j)}\) sobre la probabilidad es: \[ \frac{\partial \mathbb{E}(Y|X)}{\partial X^{(j)}} = f(X_i' \beta) \cdot \beta_{(j)} \]
Comparación con LPM:
- En el LPM, el efecto marginal es simplemente \(\beta_{(j)}\), ya que \(\frac{\partial \mathbb{E}(Y|X)}{\partial X^{(j)}} = \beta_{(j)}\).
Evaluación de Efectos Marginales:
- El efecto depende de \(f_i=f(X_i\beta)\). Puede emplearse el promedio de \(X^{(j)}\). Alternativamente, calcular todos los \(f_i\) para cada \(X_i\) y luego computar el promedio.
Variable dependiente binaria: Probit y Logit
Modelo de Utilidad Aleatoria
- Motivación Alternativa:
- Los modelos de elección binaria también pueden derivarse del enfoque de utilidad aleatoria.
- Este modelo parte de la idea de que un individuo elige entre dos opciones (\(j = \{0, 1\}\)), y cada opción le proporciona un cierto nivel de utilidad.
- Estructura del Modelo:
- La utilidad de cada opción se compone de:
- Una parte determinística que se puede predecir a partir de características observables, \(X_i'\beta^{(j)}\).
- Una parte aleatoria que representa factores no observables, \(e_i^{(j)}\).
- La utilidad de cada opción se compone de:
- Regla de Decisión del Individuo:
- El individuo elegirá la opción \(j=1\) si le genera una mayor utilidad que la opción \(j=0\).
- Es decir: \[ X_i'\beta^{(1)} + e_i^{(1)} > X_i'\beta^{(0)} + e_i^{(0)} \]
Variable dependiente binaria: Probit y Logit
Modelo de Utilidad Aleatoria (cont.)
- Simplificación del Problema:
- Podemos expresar la diferencia de utilidades entre las opciones como: \[ X_i' \beta = X_i' (\beta^{(1)} - \beta^{(0)}) > (e_i^{(0)} - e_i^{(1)}) \]
- Esto implica que el individuo elige \(j=1\) si \(X_i'\beta\) supera un umbral definido por \((e_i^{(0)} - e_i^{(1)})\).
- Derivación de la Probabilidad:
- Si asociamos una función de distribución acumulada a la parte aleatoria compuesta \((e_i^{(0)} - e_i^{(1)})\), tenemos: \[ \Pr(Y = 1) = F(X_i' \beta) \]
- Esta expresión es idéntica a la del modelo de probabilidad binaria (logit/probit) planteado al inicio.
Intuición: La elección del individuo puede modelarse como una comparación entre la utilidad esperada de cada opción, considerando tanto factores observables como no observables.
Nota: El modelo puede ampliarse a elecciones multinomiales y se aplica ampliamente en modelos de elección discreta.
Variable dependiente binaria: Probit y Logit
Software:
- Stata:
probitpara Probit ylogitpara Logit. Aunque, de forma mas general, recordemos que se puede usan MLE al crear un programa en Stata y usar el comandoml. - R:
glmde la libreria ‘stats’. Aunque, de forma mas general, recordemos que se puede usan MLE al crear una función en R y usar la librearia o paquetemaxLik.
Variable dependiente binaria en Stata (probit y logit)
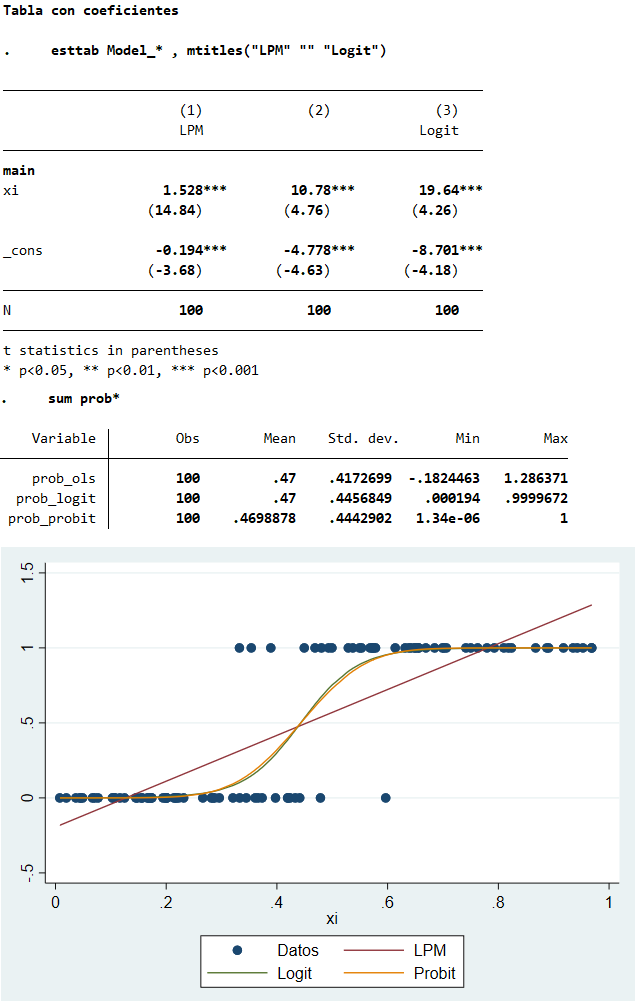
Variable dependiente binaria en Stata (comando ml)
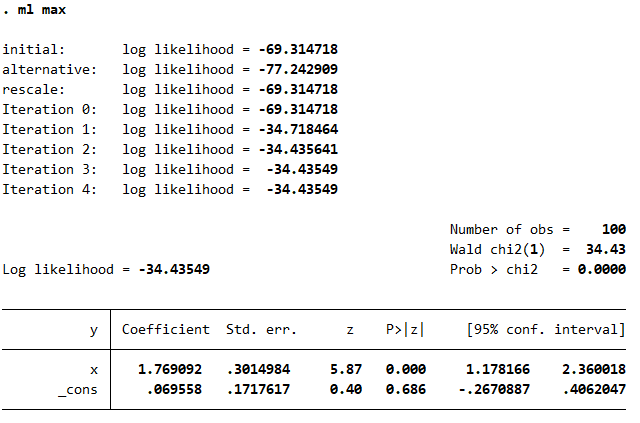
Parte computacional en
Nivel usuario: glm()
# 1. Simular datos
set.seed(123)
nobs <- 100
x <- rnorm(nobs)
y <- rbinom(n=nobs, size=1, prob=pnorm(x))
# 2. Comparar LMP / Logit / Probit
lpm <- lm(y~x)
logit <- glm(y~x, family=binomial(link="logit"))
probit<- glm(y~x, family=binomial(link="probit"))
library(stargazer)
stargazer(lpm, logit, probit, type="text")
# Comparación usando mfx
library(mfx)
logitmfx(y~x, data=data.frame(cbind(y,x)))##
## ============================================================
## Dependent variable:
## ----------------------------------------
## y
## OLS logistic probit
## (1) (2) (3)
## ------------------------------------------------------------
## x 0.303*** 2.083*** 1.186***
## (0.044) (0.447) (0.234)
##
## Constant 0.603*** 0.683** 0.376**
## (0.040) (0.269) (0.152)
##
## ------------------------------------------------------------
## Observations 100 100 100
## R2 0.326
## Adjusted R2 0.319
## Log Likelihood -45.679 -45.875
## Akaike Inf. Crit. 95.358 95.750
## Residual Std. Error 0.400 (df = 98)
## F Statistic 47.369*** (df = 1; 98)
## ============================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
## Call:
## logitmfx(formula = y ~ x, data = data.frame(cbind(y, x)))
##
## Marginal Effects:
## dF/dx Std. Err. z P>|z|
## x 0.433156 0.085583 5.0612 4.166e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Parte computacional en
Nivel intermedio: maxLik
# Código de programación en R (by luischanci)
library(maxLik)
# 1. Simulate data
set.seed(123)
nobs <- 100
x <- rnorm(nobs)
y <- rbinom(n = nobs, size = 1, prob = pnorm(x))
# 2. Define the log-likelihood function
probit_loglik <- function(params) {
beta0 <- params[1]
beta1 <- params[2]
mu <- beta0 + beta1 * x
# Log-likelihood components
ll_1 <- log(pnorm(mu))[y == 1]
ll_0 <- log(1 - pnorm(mu))[y == 0]
return(sum(ll_1, ll_0))
}
# 3. Estimate parameters using MaxLik
inicial <- c(0.1, 0.1)
probit_mle <- maxLik(logLik = probit_loglik, start = inicial)
summary(probit_mle)## --------------------------------------------
## Maximum Likelihood estimation
## Newton-Raphson maximisation, 5 iterations
## Return code 1: gradient close to zero (gradtol)
## Log-Likelihood: -45.8751
## 2 free parameters
## Estimates:
## Estimate Std. error t value Pr(> t)
## [1,] 0.3758 0.1517 2.477 0.0133 *
## [2,] 1.1859 0.2321 5.110 3.23e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## --------------------------------------------Variable dependiente elección:
Logit/Probit Multinomial (y Ordenado)
Variable Dependiente Elección Múltiple
Introducción
- Generalización de Logit/Probit:
- Vamos a extender los modelos logit/probit binarios a aquellos casos en los que la variable dependiente puede tomar más de dos valores.
- En particular, consideraremos opciones categóricas donde el conjunto de opciones es mayor a dos.
- Enfoque Probabilístico:
- Al igual que en los modelos binarios, asociamos funciones de probabilidad acumulada a cada elección.
- Utilizaremos el método de Máxima Verosimilitud (MLE) para estimar los parámetros, planteando y maximizando la función de verosimilitud correspondiente.
Referencia: Esta sección sigue el capítulo 15 de Cameron y Trivedi (2005).
Variable Dependiente Elección Múltiple
Introducción
- Respuestas Múltiples No Ordenadas:
- En este caso, las opciones no tienen un orden específico o jerarquía.
- También se conoce como Regresión Logística Multinomial o Multinomial Logit.
- Ejemplos:
- ¿Qué medio de transporte utiliza para ir al trabajo?
- 1: Metro
- 2: Bus
- 3: Bicicleta
- ¿Por cuál partido votará en las próximas elecciones?
- 1: Partido de Derecha
- 2: Partido de Centro
- 3: Coalición de Izquierda
- ¿Qué medio de transporte utiliza para ir al trabajo?
- En este caso, las opciones no tienen un orden específico o jerarquía.
Variable Dependiente Elección Múltiple
Introducción
- Respuestas Ordenadas:
- Aquí, las opciones tienen un orden implícito.
- Este tipo de modelo se conoce como Logit/Probit Ordenado.
- Ejemplos:
- ¿Cómo evaluaría la calidad del servicio recibido?
- 1: Excelente
- 2: Bueno
- 3: Malo
- ¿Cómo evaluaría la calidad del servicio recibido?
- Aquí, las opciones tienen un orden implícito.
Variable Dependiente Elección Múltiple
Multinomial Logit
Variable Dependiente Elección Múltiple
Multinomial Logit
- Descripción General:
- Este modelo es adecuado cuando la variable dependiente incluye más de dos alternativas cualitativas sin ningún tipo de orden implícito.
- Ejemplo: Elegir un lugar para pescar, donde \(y_i \in \{\text{playa}, \text{bote}, \text{muelle}\}\).
- Enfoque de Utilidad Aleatoria:
- Siguiendo el marco de los modelos de utilidad aleatoria, se modela la probabilidad de escoger una opción particular sobre las demás, dadas las características observables.
- Una forma de extender el modelo es comparar pares de opciones, como en el logit binario, asignando una probabilidad a cada comparación.
Variable Dependiente Elección Múltiple: Multinomial Logit
- Función de Distribución de Probabilidad (f.d.p.):
- Se usa la f.d.p. logística, en lugar de la normal, ya que es computacionalmente más sencilla y adecuada para este contexto.
- Estructura del Modelo:
Supongamos que existen \(J + 1\) alternativas, donde se designa una categoría como base de comparación.
Las funciones de probabilidad para cada alternativa son:
Para la categoría base \(Y=0\): \[ Pr(Y=0|\boldsymbol{X}) = \frac{1}{\left[1 + \sum_{j=1}^J \exp(X \beta^{(j)})\right]} \]
Para cualquier otra categoría \(Y=j\), con \(j=1,...,J\): \[ Pr(Y=j|\boldsymbol{X}) = \frac{\exp(X \beta^{(j)})}{\left[1 + \sum_{j=1}^J \exp(X \beta^{(j)})\right]} \]
Variable Dependiente Elección Múltiple: Multinomial Logit
Interpretación de los Coeficientes:
- Los coeficientes \(\beta^{(j)}\) varían por opción, lo que significa que cada alternativa tiene su propio conjunto de parámetros.
- Si \(J = 1\), el modelo se reduce a un logit binario, donde solo hay dos opciones.
Log de los Coeficientes:
- La relación de los logaritmos de las probabilidades se expresa como: \[\ln \left( \frac{P_{ij}}{P_{i0}} \right) = X_i' \beta^j\]
- Alternativamente, normalizando respecto a otra probabilidad ( k ): \[\ln \left( \frac{P_{ij}}{P_{ik}} \right) = X_i' (\beta^j - \beta^k)\]
Con estas probabilidades, se pueden construir modelos que expliquen la preferencia por una opción sobre otras a partir de las características observables y la estructura de utilidades latentes.
Variable Dependiente Elección Múltiple: Multinomial Logit
Independencia de Alternativas Irrelevantes (IAI)
Los modelos multinomiales como el logit asumen la independencia de alternativas irrelevantes (IAI). Esto significa que la relación de probabilidades entre dos opciones es independiente de la presencia o ausencia de otras alternativas.
Como vimos, para dos respuestas \(k\) y \(r\), la razón de probabilidades se expresa como: \[\frac{Pr(Y_i = k)}{Pr(Y_i = r)} = \exp \left( X_i' (\beta^k - \beta^r) \right)\]
- Esto implica que la relación entre las probabilidades de escoger las opciones \(k\) y \(r\) no depende de las características de otras alternativas en el conjunto de opciones.
- La propiedad de IAI implica que adicionar o remover alternativas en el conjunto de opciones no afecta la relación de probabilidades entre dos opciones específicas, como \(k\) y \(r\).
Este supuesto facilita la estimación y análisis de los modelos, pero también limita la flexibilidad del modelo en situaciones donde las alternativas pueden estar correlacionadas o donde la presencia de otras opciones influye en la elección relativa entre dos opciones.
Variable Dependiente Elección Múltiple: Multinomial Logit
Función de Verosimilitud La función de verosimilitud a maximizar es:
\[\mathcal{L} = \sum_{i=1}^N \sum_{j=0}^J d_{ij} \cdot \ln \left( P(Y_i = j) \right)\]
Donde \(d_{ij}\) es una variable indicadora (dummy) que toma el valor de 1 si el individuo \(i\) escoge la alternativa \(j\), y 0 en caso contrario.
Condiciones de Primer Orden: Las condiciones necesarias de primer orden para maximizar la verosimilitud son: \[\frac{\partial \mathcal{L}}{\partial \beta^j} = \sum_i (d_{ij} - P_{ij}) \cdot X_i \quad \text{para } j = 1, \ldots, J\]
Variable Dependiente Elección Múltiple
Logit Condicional
El modelo de Logit Condicional es una extensión del logit multinomial que permite que las probabilidades de elección dependan no solo de las características individuales, sino también de las características específicas de cada alternativa. Ambos modelos permiten manejar múltiples alternativas no ordenadas, pero el logit condicional incorpora explícitamente características de cada opción.
El modelo logit condicional es útil en contextos donde las opciones de elección tienen características propias que influyen en la decisión del individuo. Ejemplos:
- Elección de medios de transporte en función de atributos como el costo, tiempo de viaje, y comodidad de cada opción (metro, bus, bicicleta, etc.).
- Elección de lugar de compra basado en factores como precio, distancia, y calidad del servicio en cada tienda.
Referencia: Ver capítulo 15 en Cameron y Trivedi para una discusión detallada.
Variable Dependiente Elección Múltiple: Logit Condicional
Probabilidad de Elección y función de verosimilitud
- La probabilidad de que el individuo \(i\) elija la alternativa \(j\) se define como: \[ P_{ij} = \frac{\exp(X_{ij}' \beta)}{\sum_{v=1}^J \exp(X_{iv}' \beta)} \]
- Aquí, \(X_{ij}\) representa las características observables de la alternativa \(j\) para el individuo \(i\).
- La interpretación es que el vector de parámetros \(\beta\) es común para todas las alternativas, pero las características específicas varían entre opciones.
- La función de verosimilitud para el logit condicional, dada la elección observada, es: \[ \mathcal{L} = \prod_{i=1}^N \prod_{j=0}^J \left( \frac{\exp(X_{ij}' \beta)}{\sum_{k=1}^J \exp(X_{ik}' \beta)} \right)^{d_{ij}} \] Donde \(d_{ij}\) es una variable indicadora que toma el valor de 1 si el individuo \(i\) elige la alternativa \(j\), y 0 en caso contrario.
Variable Dependiente Elección Múltiple
Multinomial Probit
El modelo de Multinomial Probit es una alternativa al Multinomial Logit cuando se desea incorporar correlación entre alternativas.
A diferencia del multinomial logit, el multinomial probit no asume Independencia de Alternativas Irrelevantes (IAI). Esto significa que la relación de probabilidades entre dos opciones sí puede depender de la presencia o ausencia de otras alternativas.
El Multinomial Probit permite relajarse del supuesto de IAI ya que modela la correlación entre los errores de las alternativas mediante una distribución normal multivariada. Esto permite una mayor flexibilidad en escenarios donde las alternativas son similares y podrían estar correlacionadas, como en la elección de diferentes marcas o modos de transporte.
Variable Dependiente Elección Múltiple: M. Probit
En el multinomial probit, la probabilidad de elegir una alternativa involucra múltiples integrales de la función de densidad normal multivariada. Esto genera un problema de alta complejidad computacional debido a la necesidad de calcular integrales múltiples.
Por ejemplo, para un modelo con tres alternativas, la probabilidad de elegir una de ellas está dada por: \[ Pr(Y_i = 1) = \iint f(u_{i2}, u_{i3}) \, du_{i2} \, du_{i3} \]
Aquí, \(f(u_{i2}, u_{i3})\) representa la función de densidad conjunta de una distribución normal bivariada. A medida que aumenta el número de alternativas, el número de integrales necesarias también aumenta, lo que complica el cálculo.
En la práctica, para resolver este problema, se emplean técnicas de simulación como el Método de Simulación de Máxima Verosimilitud (ML) o métodos basados en Monte Carlo para aproximar las probabilidades.
Variable Dependiente Elección Múltiple: M. Probit
Función de Verosimilitud Similar al multinomial logit, el modelo multinomial probit utiliza una función de verosimilitud para estimar los parámetros. Sin embargo, debido a las integrales mencionadas, la maximización de la verosimilitud es considerablemente más complicada. La función de verosimilitud, en este caso, requiere aproximaciones numéricas para poder resolver los múltiples integrales.
Nota: La elección entre el multinomial logit y el multinomial probit depende de la aplicación específica y la disponibilidad de recursos computacionales. Si las alternativas son claramente diferenciables y no correlacionadas, el logit multinomial puede ser suficiente y más práctico.
Variable Dependiente Elección Múltiple
Software:
- Stata:
mprobitpara Multinomial Probit,mlogitpara Multinomial Logit yclogitpara Logit Condicional. - R:
multinomde la libreria ‘nnet’,mlogitde la libreria ‘mlogit’,clogitde la libreria ‘survival’. Otros sonMNPybayesm. Pero para grandes bases, tal vez elmlogitsea más eficiente.
Variable Dependiente Elección Múltiple en Stata
Uso de mlogit, mfx y margins:
* Datos a usar
use multinomial_15, clear
tab mode
/* Elección donde pescar:
1. playa
2. muelle
3. botepriv
4. charter */
* Estimación Multinomial Logit
/* Todos comparados con la opc 1, (b_j - b_k) */
mlogit mode income, baseoutcome(1)
/* Prob. predichas */
predict p1 p2 p3 p4,pr
summarize dbeach p1 ///
dpier p2 ///
dprivate p3 ///
dcharter p4
/* Marginal effects (or semi-elasticities) */
mfx compute, dydx predict(outcome(1))
/* Average Marginal effects (AME) */
margins, dydx(income) predict(outcome(1)) atmeans
/* Marginal Effects at Means (MEM) */
margins, dydx(income) predict(outcome(1)) 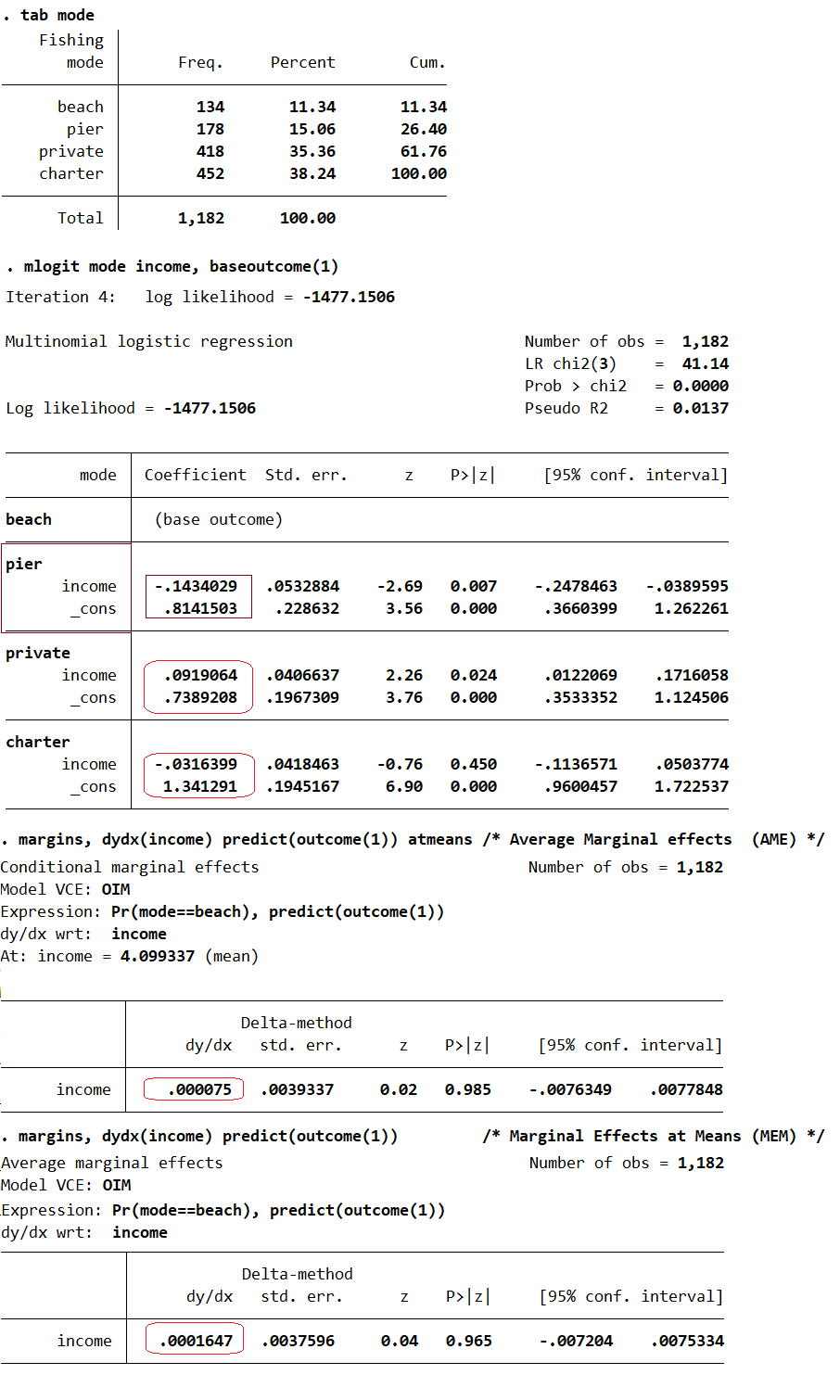
Variable Dependiente Elección Múltiple en
# Datos a usar
Data <- as.data.frame(haven::read_dta('multinomial_15.dta'))
#table(Data$mode)
Data$mode <- factor(Data$mode)
# Estimación Multinomial Logit
library(nnet)
set.seed(123)
Data$mode <- relevel(Data$mode, ref = 1) # baseline
reg.mlogit <- multinom(mode ~ income, data = Data)
summary(reg.mlogit) # Rel. Log Odds
exp(coef(reg.mlogit)) # Rel. risk# Prob. predichas
Data <- Data%>%
mutate(
p1 = predict(reg.mlogit, newdata = Data, type = "probs")[, 1],
p2 = predict(reg.mlogit, newdata = Data, type = "probs")[, 2],
p3 = predict(reg.mlogit, newdata = Data, type = "probs")[, 3],
p4 = predict(reg.mlogit, newdata = Data, type = "probs")[, 4]
)
#Data|>
#summarize(
#p1_mean = mean(p1, na.rm = TRUE), p2_mean = mean(p2, na.rm = TRUE),
#p3_mean = mean(p3, na.rm = TRUE), p4_mean = mean(p4, na.rm = TRUE))
# Marginal effects (or semi-elasticities)
library(marginaleffects)
mfx <- slopes(reg.mlogit, variables = "income", type = "probs")
summary(mfx$estimate)Estimación:
## # weights: 12 (6 variable)
## initial value 1638.599935
## iter 10 value 1477.505846
## final value 1477.150569
## converged
## Call:
## multinom(formula = mode ~ income, data = Data)
##
## Coefficients:
## (Intercept) income
## 2 0.8141701 -0.14340453
## 3 0.7389569 0.09190030
## 4 1.3413284 -0.03164588
##
## Std. Errors:
## (Intercept) income
## 2 0.2286325 0.05328822
## 3 0.1967314 0.04066362
## 4 0.1945173 0.04184622
##
## Residual Deviance: 2954.301
## AIC: 2966.301
## (Intercept) income
## 2 2.257301 0.8664035
## 3 2.093750 1.0962555
## 4 3.824120 0.9688496Efectos marginales:
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.027804 -0.015947 -0.003621 0.000000 0.009032 0.033632Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
En algunos casos, la variable dependiente es una variable categórica con más de dos alternativas y un orden natural entre las categorías.
A diferencia del multinomial logit, donde las opciones no tienen un orden particular, en el modelo de respuesta múltiple ordenada se aprovecha el orden implícito entre las categorías.
Los modelos Ordered Logit y Ordered Probit son extensiones de los modelos logit y probit tradicionales para tratar con variables dependientes ordinales.
Ejemplos:
- Un cliente califica su satisfacción con un producto o servicio en una escala ordinal:
1. Insatisfecho; 2. Neutral; 3. Satisfecho; 4. Muy Satisfecho - Un individuo alcanza un nivel de educación que se puede ordenar de menor a mayor:
1. Primaria; 2. Secundaria; 3. Pregrado; 4. Posgrado
La interpretación del modelo se centra en analizar cómo los cambios en las variables explicativas influyen en la probabilidad de moverse hacia categorías superiores o inferiores.
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
Los modelos de respuesta múltiple ordenada parten de una variable latente \(Y^*\), que representa la propensión subyacente de una persona a seleccionar una categoría más alta o baja.
La variable latente se modela como \(Y^* = X\beta + u\), donde \(X\) son las variables explicativas (observables) and \(u_i\) es el término de error (asumido con distribución normal o logística).
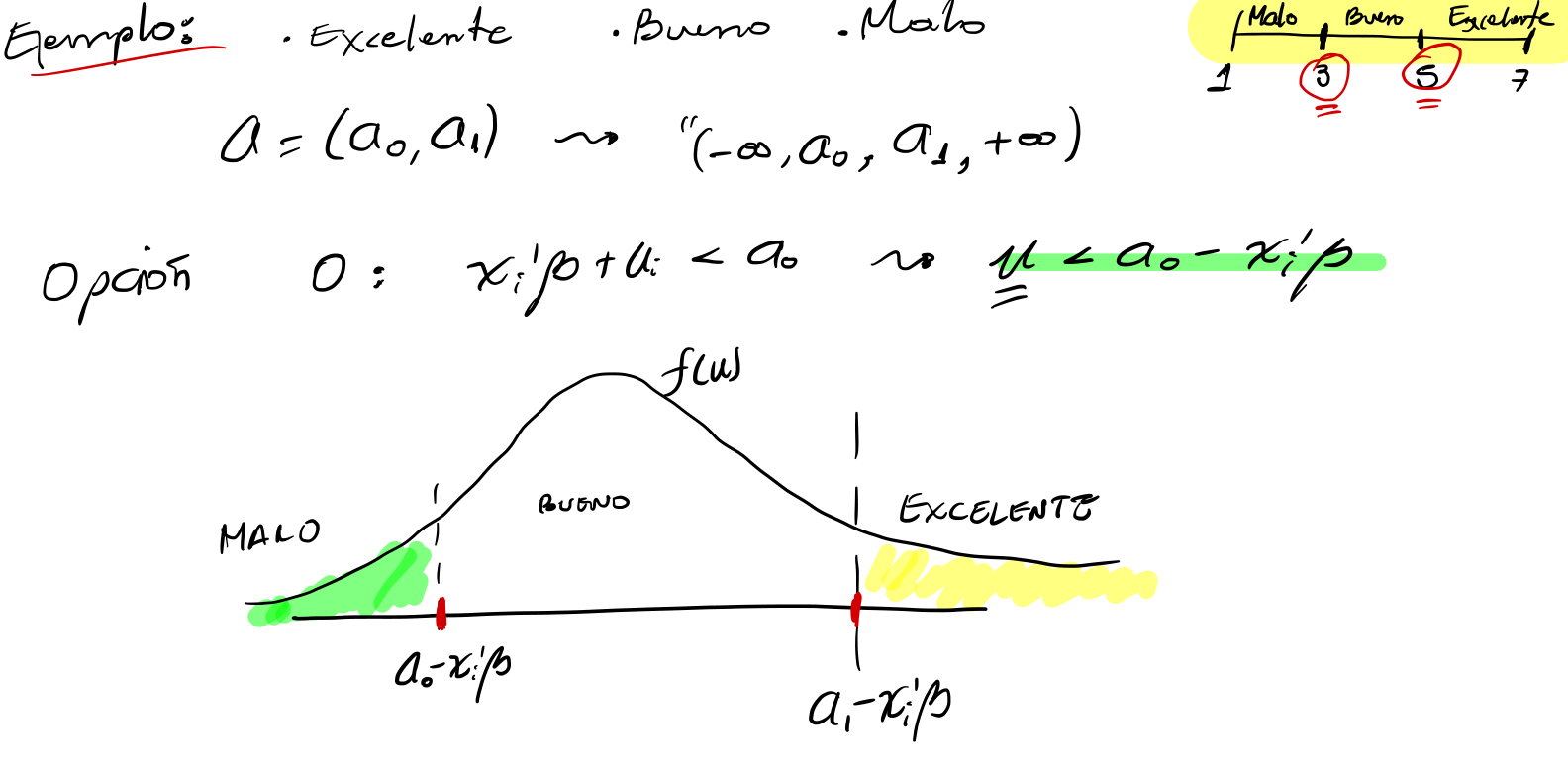
La variable dependiente observada \(Y\) es una versión ordinal de \(Y^*\), donde cada valor de \(Y\) se asocia a un rango específico de \(Y^*\).
\[Y_i = \begin{cases} 0 & \text{si } Y_i^* < A_0 \\ 1 & \text{si } A_0 \leq Y_i^* < A_1 \\ \vdots \\ J & \text{si } A_{J-1} \leq Y_i^* < A_J \end{cases} \]
los umbrales \(A\) representan los puntos de corte que delimitan las categorías.
Así, los parámetros a estimar son: \(\beta\) junto a los \(A=(A_0,\ldots,A_{J-1})\) umbrales.
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
La probabilidad de que un individuo elija una categoría en particular se calcula mediante la función de distribución acumulada de la normal estándar (para el probit ordenado) o de la logística (para el logit ordenado).
La probabilidad de que \(Y_i = j\) está dada por:
\[\begin{eqnarray} Pr(Y_i = 0) &=& F(a_0 - X_i'\beta) \\ Pr(Y_i = j) &=& F(a_j - X_i'\beta) - F(a_{j-1} - X_i'\beta), \quad j > 0 \\ Pr(Y_i = J) &=& 1 - F(a_{J-1} - X_i'\beta) \end{eqnarray}\]
\(F(\cdot)\) representa la función de distribución acumulada, por ejemplo, la normal acumulada en el caso del Probit o la logística acumulada en el caso del Logit ( \(F(z)=[1+exp(-z)]^{-1}\) ).
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
La función de verosimilitud a maximizar es:
\[ \mathcal{L}(\beta, a) = \prod_{i=1}^N \prod_{j=0}^J \left( Pr(Y_i = j) \right)^{d_{ij}} \]
donde \(d_{ij}\) es una variable indicadora que toma valor 1 si \(Y_i = j\) y 0 en caso contrario.
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
Solo para resaltar algo acá: tanto el logit multinomial como el logit ordenado tienen una forma similar para la log-verosimilitud.
Aunque la estructura de la log-verosimilitud es la misma, la elección de la función de probabilidad refleja las suposiciones del modelo sobre la naturaleza de las opciones (no ordenadas vs. ordenadas).
La diferencia radica en la expresión para \(P(Y_i = j)\):
- Logit Multinomial: \(P(Y_i = j)\) se calcula usando la función logística multinomial: \[ P(Y_i = j) = \frac{\exp(X_i' \beta_j)}{\sum_{k=1}^J \exp(X_i' \beta_k)} \]
- Logit Ordenado: \(P(Y_i = j)\) se basa en probabilidades acumuladas, típicamente usando la función de distribución logística acumulada: \[ P(Y_i = j) = F(a_j - X_i' \beta) - F(a_{j-1} - X_i' \beta) \]
En el logit multinomial, los coeficientes \(\beta_j\) varían por opción, capturando la preferencia relativa para cada opción; en el logit ordenado, el coeficiente \(\beta\) es constante y las probabilidades de las categorías ordenadas dependen de los umbrales \(a_j\), que segmentan la variable latente en categorías ordenadas.
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
Los efectos marginales
En los modelos logit y probit ordenados, los coeficientes no representan cambios marginales directos en las probabilidades de cada categoría. En su lugar, indican el efecto de un cambio en las variables explicativas sobre la probabilidad de moverse a categorías superiores o inferiores.
\[ \frac{\partial Pr(Y_i = j)}{\partial X_r} = \left[ F'(a_j - X_i'\beta) - F'(a_{j-1} - X_i'\beta) \right] \cdot \beta_r \]
Notar que varían según el punto de evaluación, usualmente en la media de \(X\) o en valores específicos.
Variable Dependiente Elección Múltiple:
Respuesta Múltiple Ordenada
Software:
- Stata:
oprobitpara Probit Ordenado,ologitpara Logit Ordenado. - R:
polrde la libreria MASS
Poisson Regression: Modelo para variables de conteo.
Regresión de Poisson
- Regresión de Poisson
- Modelo de regresión para datos de conteo, donde la variable dependiente representa el número de eventos en un tiempo o espacio específico.
- Los datos de conteo son no negativos y discretos (0, 1, 2,…).
- Ejemplos:
- Número de cervezas que se venden en un bar entre las 23:00 y las 00:00 horas.
- Número de accidentes de tráfico en una intersección por día.
- Número de llamadas telefónicas recibidas por un centro de atención al cliente por minuto.
Regresión de Poisson
El modelo de probabilidad esta dado por:
Función de Probabilidad: \[P(Y = y) = \frac{e^{-\lambda} \lambda^y}{y!}, \quad y = 0, 1, 2, ...\]
\(Y\) es variable discreta que representa el número de eventos; \(\lambda\) es la media.
Para hacerlo un modelo de regresión: - Relación entre Media y Variables Independientes: \[\lambda = E(Y|X) = e^{X'\beta}\] donde \(X = (X_1, X_2, ..., X_k)'\) es un vector de variables explicativas. - Supuesto Clave: \(Y\) sigue una distribución de Poisson con media \(\lambda\), donde \(\lambda\) es función de \(X\).
Regresión de Poisson
- Coeficientes (\(\beta_j\)):
- Representan el cambio en el logaritmo de la media de \(Y\) por un cambio de una unidad en \(X_j\), manteniendo constantes las demás variables.
- \(\exp(\beta_j)\) representa el cambio multiplicativo en la media de \(Y\) con un cambio unitario en \(X_j\).
- Ejemplo: Si \(\exp(\beta_1) = 1,2\), un aumento de una unidad en \(X_1\) se asocia con un aumento del 20% en la media de \(Y\).
Regresión de Poisson
Función de Verosimilitud: \[L(\beta) = \prod_{i=1}^{n} \frac{e^{-\lambda_i} \lambda_i^{y_i}}{y_i!}\] donde \(\lambda_i = e^{X_i'\beta}\).
Log-Verosimilitud: \[\ell(\beta) = \sum_{i=1}^{n} (y_i X_i'\beta - e^{X_i'\beta} - \ln(y_i!))\]
Regresión de Poisson
Inferencia
- Errores Estándar: Se calculan a partir de la matriz de información de Fisher.
- Pruebas de Hipótesis: Se pueden realizar pruebas t para la significancia individual de los coeficientes y pruebas de Wald para restricciones conjuntas.
- Intervalos de Confianza: Se construyen intervalos de confianza para los coeficientes.
Regresión de Poisson
Sobredispersión La sobredispersión ocurre cuando la varianza de \(Y\) es mayor que su media, violando el supuesto de Poisson.
- Causas:
- Heterogeneidad no observada.
- Omisión de variables relevantes.
- Eventos correlacionados.
- Consecuencias:
- Sesgo en estimaciones de errores estándar.
- Pruebas de hipótesis incorrectas.
- Soluciones:
- Regresión Binomial Negativa: Modelo alternativo para permitir sobredispersión.
- Estimación Robusta: Ajuste de errores estándar para sobredispersión.
Regresión de Poisson
Software:
- Stata:
rpoisson - R:
glm
Variable Dependiente Elección Múltiple en Stata
Uso de ml y de comando poisson:
* Ejemplo reg. poisson Stata por L.Chancí
* 1. Simulamos la Data
set seed 123
set obs 1000
gen x = rnormal(0, 1) // Supongamos es ingreso
scalar b0 = 1 // Intercepto
scalar b1 = 0.5 // Pendiente
gen lambda = exp(b0 + b1 * x) // Ej. la media de crímenes
gen y = rpoisson(lambda) // Ej. Número de crímenes
sum y
hist y, freq title(Hist. crímenes en la ciudad) color(navy)
* 2. Log-likelihood fn.
cap pro drop chanci_llf
prog def chanci_llf
args lnf xb
tempname mu
gen double `mu' = exp(`xb')
qui replace `lnf' = -`mu' + y * `xb' - lnfactorial(y)
drop `mu'
end
ml model lf chanci_llf (y = x)
ml max
* 4. Comparamos con comando
poisson y x /* , vce(robust) */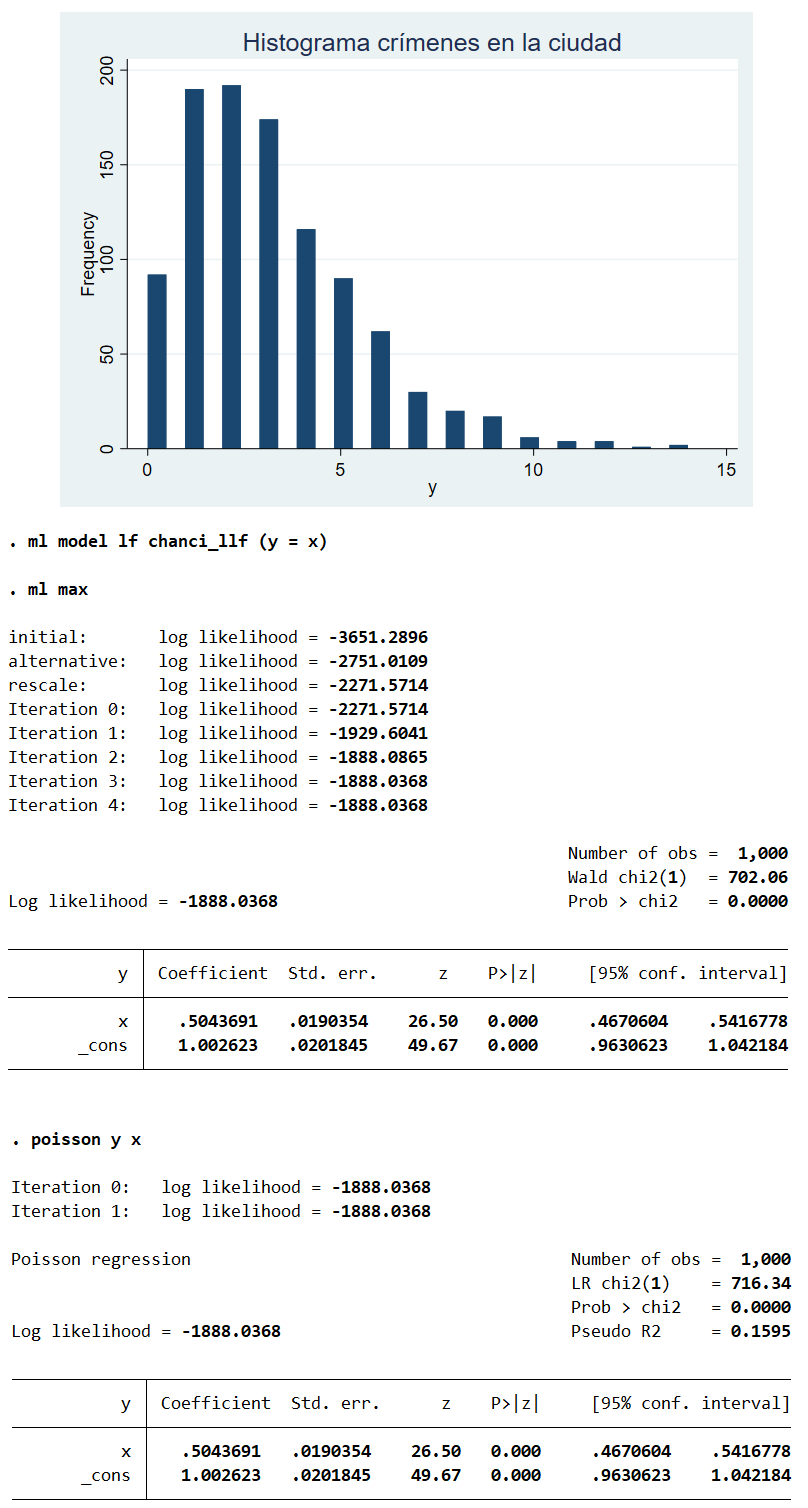
Variable Dependiente Elección Múltiple en
# 1. Estimación
library(maxLik)
ch_ll<- function(params) {
b0 <- params[1]
b1 <- params[2]
xb <- b0 + b1 * x
mu <- exp(xb)
ll <- -mu + y * xb - lfactorial(y)
return(sum(ll))
}
mle_poisson <- maxLik(logLik=ch_ll, start=c(0.1, 0.1))
summary(mle_poisson)
# 3. Compare with Built-in glm Poisson Regression
glm(y ~ x, family = poisson(link = "log"))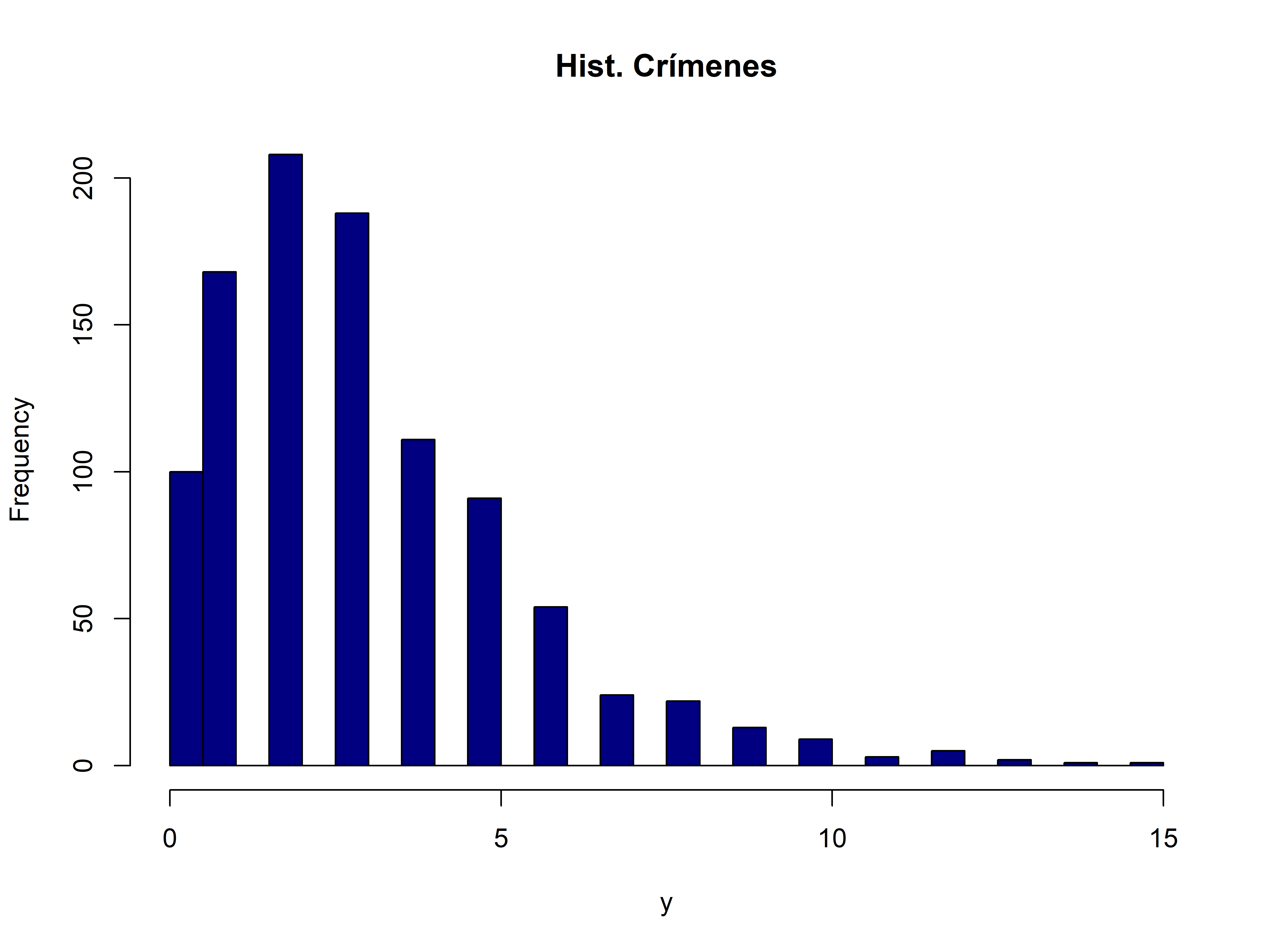
## --------------------------------------------
## Maximum Likelihood estimation
## Newton-Raphson maximisation, 4 iterations
## Return code 8: successive function values within relative tolerance limit (reltol)
## Log-Likelihood: -1889.833
## 2 free parameters
## Estimates:
## Estimate Std. error t value Pr(> t)
## [1,] 1.00000 0.02012 49.71 <2e-16 ***
## [2,] 0.47950 0.01802 26.61 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## --------------------------------------------
##
## Call: glm(formula = y ~ x, family = poisson(link = "log"))
##
## Coefficients:
## (Intercept) x
## 1.0000 0.4795
##
## Degrees of Freedom: 999 Total (i.e. Null); 998 Residual
## Null Deviance: 1845
## Residual Deviance: 1140 AIC: 3784Censura y Truncamiento
Tobit, Heckman
Censura y Truncamiento
Variable dependiente observada en forma incompleta o limitada
Introducción
- En estos modelos, la variable de interés
Yes continua (nuevamente). - Sin embargo, por alguna razón, la variable
Yestá incompleta:- Truncada o censurada.
- OLS no es válido ya que la muestra no es representativa de la población.
Censura y Truncamiento
Truncamiento:
- Observaciones sistemáticamente excluidas (var. dep. \(y\) explicativas eliminadas o perdidas). Es decir, no hay datos completos.
Ejemplo: Encuesta de hogares donde no se incluye a hogares con ingresos muy altos. Por alguna razón, la muestra de ingreso de hogares no incluye los hogares que ganan 10 millones de pesos al mes.
Censura:
- Todas las observaciones son incluidas. Sin embargo, la variable dependiente \(y\) se observa dentro de un rango; por encima o por debajo de cierto umbral son tratados como si estuvieran en el umbral.
Ejemplo: Encuesta de hogares donde se reemplaza ingreso con “ingreso es mayor a 10” por un valor. Usando el ejemplo hipotético de la encuesta de hogares, diciendo que en los datos de “ganar mil millones”, un millón es lo máximo, donde “ganar un millón” está registrado como ese umbral.
Censura y Truncamiento
Truncamiento incidental a sesgo de selección
- Truncamiento: Caso donde la muestra se relaciona de forma muy alejada con la variable de interés. Ejemplo: Encuesta de innovación de Chile que solo incluye a las empresas que innovan.
- Sesgo de Selección: Estudio de salarios solo con datos de mujeres que trabajan. La decisión de trabajar no es aleatoria y depende del nivel de la variable de interés.
Ejemplo: Heckman (1979). El ejemplo más famoso es el de Heckman, donde el valor es implícito en la oferta de empleo. Sin embargo, estudios de salarios solo usan datos de mujeres que trabajan. Pero, la decisión de trabajar no es aleatoria. Es decir, en principio, se necesita incluir trabajadores que no trabajan.
Censura
Nuestro gran objetivo es plantear la función de verosimilitud, así que partamos por entender el contexto del modelo.
Mecanismo:
Sea \(y\) el valor observado, la parte incompleta de \(y^*\).
En censura observamos toda la información de \(X_i\), pero la censura en \(y^*\) puede ser:
- Censura por debajo: \[ y = y^* \text{ si } y^* > L \text{ y } y = L \text{ si } y^* \leq L \]
- Por ejemplo, \(L = 0\) en una encuesta de gasto en bienes durables.
- Si \(y^* \leq L\), entonces \(y\) toma el valor de \(L\). Si \(y^* > L\), entonces \(y = y^*\).
Censura
- Censura por encima: \[ y = y^* \text{ si } y^* \leq U \text{ y } y = U \text{ si } y^* > U \]
- Por ejemplo, en una encuesta de hogares con ingreso mayor a \(U = 10^6\).
- Si \(y^* > U\), entonces \(y\) toma el valor de \(U\). Si \(y^* \leq U\), entonces \(y = y^*\).
Notas:
- Supongamos que en los datos solo vemos la variable dependiente hasta un umbral. Por ejemplo, ingresos hasta un millón: todos los ingresos reportan \(< U\) y los ingresos mayores se consideran censurados.
- Censura superior o inferior. Ejemplo: censura por debajo en los ingresos cuando \(L = 0\). En este caso: para deuda negativa sustituimos 0.
Censura
Función de densidad con censura: Para \(y^*\), la función de densidad \(f^*(y^*|x, \theta)\) se define de la forma usual, donde \(\theta\) representa los parámetros del modelo. Sin embargo, para la variable observada \(y\), la densidad se ajusta para considerar la censura.
Censura por debajo en \(L\)
Para los valores de \(y > L\), la densidad de \(y\) es la misma que la densidad de \(y^*\): \[ f(y|x) = f^*(y|x,\theta) \text{ si } y > L\]
Para \(y \leq L\), la densidad de \(y\) se concentra en el punto \(L\): \[ f(y|x) = P(y^* \leq L | x, \theta) = F^*(L | x, \theta) \text{ si } y = L\]
donde \(F^*(L | x, \theta)\) es la función de distribución acumulada de \(y^*\) evaluada en \(L\).
Censura
Función de Verosimilitud: Para una observación \(i\), la contribución a la función de verosimilitud se define como:
\[ L_i(\theta) = \begin{cases} f^*(y_i | x_i, \theta) & \text{si } y_i > L \\ F^*(L | x_i, \theta) & \text{si } y_i = L \end{cases} \]
Podemos escribir esto de forma compacta usando una variable indicadora \(d_i = \mathbb{I}(y_i > L)\):
\[ L_i(\theta) = [f^*(y_i | x_i, \theta)]^{d_i} \cdot [F^*(L | x_i, \theta)]^{1-d_i} \]
Log-verosimilitud: La log-verosimilitud para la muestra completa se obtiene sumando las contribuciones individuales:
\[ \ell(\theta) = \sum_{i=1}^{n} \left[ d_i \cdot \ln f^*(y_i | x_i, \theta) + (1-d_i) \cdot \ln F^*(L | x_i, \theta) \right] \]
Censura: Normalidad y Modelo Tobit
Incorporación del supuesto de Normalidad
- En muchos casos, se asume que la variable latente \(y^*\) sigue una distribución normal.
- Es importante repasar primero las propiedades estadísticas de la distribución normal censurada para comprender cómo afecta al modelo.
- Bajo el supuesto de normalidad, podemos derivar expresiones explícitas para la función de verosimilitud, lo que facilita la estimación e inferencia.
Censura: Normalidad y Modelo Tobit
Momentos de la Distribución Normal Censurada
Consideremos una variable aleatoria \(z^*\) que sigue una distribución normal con media \(\mu\) y varianza \(\sigma^2\).
Supongamos que \(z^*\) está censurada por debajo en un umbral \(L\). Esto significa que solo observamos \(z = z^*\) si \(z^* > L\), y observamos \(z = L\) si \(z^* \leq L\).
\[z^* \sim \mathcal{N}(\mu, \sigma^2) \hspace{0.5cm};\hspace{0.5cm} z = \begin{cases} z^*, & \text{si } z^* > L \\ L, & \text{si } z^* \leq L \end{cases}\]
Censura: Normalidad y Modelo Tobit
Momentos de la Distribución Normal Censurada
Momentos:
- Media: La media de la variable censurada \(z\) está dada por: \[ E(z) = \mu + \sigma \cdot \frac{\phi(\lambda)}{1-\Phi(\lambda)}, \] donde \(\lambda = (L - \mu)/\sigma\).
- Varianza: La varianza de la variable censurada \(z\) es: \[ \text{Var}(z) = \sigma^2 \left[ 1 - \frac{\phi(\lambda) \cdot (\phi(\lambda) - \lambda)}{[1-\Phi(\lambda)]^2} \right], \] donde \(\phi(\cdot)\) es la función de densidad normal estándar y \(\Phi(\cdot)\) es la acumulada normal estándar.
Censura: Normalidad y Modelo Tobit
Modelo Tobit
- El modelo Tobit es un modelo de regresión censurada donde la variable dependiente está censurada, típicamente en cero.
- Originalmente fue propuesto para soluciones de esquina (ej. adquirir un seguro agrícola).
- Es una extensión del modelo de regresión lineal que permite manejar la censura en la variable dependiente.
- Se asume que existe una variable latente \(y_i^*\) que sigue un modelo lineal con errores normales: \[ y_i^* = X_i'\beta + \varepsilon_i, \quad \varepsilon_i \sim \mathcal{N}(0, \sigma^2). \]
- La variable observada \(y_i\) es una versión censurada de \(y_i^*\): \[ y_i = \begin{cases} y_i^*, & \text{si } y_i^* > 0, \\ 0, & \text{si } y_i^* \leq 0. \end{cases}\]
Censura: Normalidad y Modelo Tobit
Modelo Tobit
Probabilidad de Censura. La probabilidad de que la variable latente sea menor o igual a cero (y por lo tanto censurada) es: \[ F^*(0) = P(y^* \leq 0) = P(\varepsilon \leq -X'\beta) = \Phi(-X'\beta/\sigma). \]
Función de log-verosimilitud. Para estimar los parámetros del modelo Tobit (\(\beta\) y \(\sigma\)), se utiliza el método de máxima verosimilitud. La función de log-verosimilitud se construye considerando la densidad de la variable observada \(y_i\), que se ajusta para tener en cuenta la censura:
\[\ell(\beta, \sigma) = \sum_{i=1}^n \left[ d_i \left(-\ln(\sqrt{2\pi} \sigma) - \frac{(y_i - X_i'\beta)^2}{2\sigma^2}\right) + (1-d_i) \ln[1 - \Phi(X_i'\beta/\sigma)] \right]\]
donde \(d_i = 1\) si \(y_i > 0\), y \(d_i = 0\) si \(y_i \leq 0\). Es decir, el primer término dentro de la suma corresponde a las observaciones no censuradas, y el segundo término a las observaciones censuradas.
Censura: Normalidad y Modelo Tobit
Modelo Tobit
Condiciones de Primer Orden (CPO) del Modelo Tobit
Derivadas de la función de log-verosimilitud respecto a los parámetros: \[ \frac{\partial \ell}{\partial \beta} = \sum_i \left[ d_i \cdot \frac{(y_i - X_i'\beta)}{\sigma^2} + (1 - d_i) \cdot \frac{\phi(X_i'\beta/\sigma)}{1 - \Phi(X_i'\beta/\sigma)} \cdot \frac{X_i}{\sigma} \right] = 0 \]
\[ \frac{\partial \ell}{\partial \sigma} = \sum_i \left[ d_i \left(-\frac{1}{\sigma} + \frac{(y_i - X_i'\beta)^2}{\sigma^3}\right) + (1 - d_i) \cdot \frac{\phi(X_i'\beta/\sigma)}{1 - \Phi(X_i'\beta/\sigma)} \cdot \frac{X_i'\beta}{\sigma^2} \right] = 0 \]
Estas ecuaciones no tienen una solución analítica cerrada y se utilizan métodos numéricos, como el algoritmo de Newton-Raphson, para encontrar las estimaciones de máxima verosimilitud de \(\beta\) y \(\sigma\).
Truncamiento
El truncamiento es un tipo de censura donde las observaciones fuera de un rango determinado se excluyen completamente de la muestra. Esto implica una pérdida de información tanto de la variable dependiente como de las variables independientes.
Tipos de Truncamiento:
Truncamiento por debajo (\(L\)): \[ y = y^* \; \text{si} \; y^* > L\] Ejemplo: Solo se incluyen observaciones con \(y^* > L\) (e.g., hogares con ingresos mayores a 10 millones).
Truncamiento por encima (\(U\)): \[ y = y^* \; \text{si} \; y^* \leq U. \] Ejemplo: Solo se incluyen hogares con ingresos menores a \(10\) millones.
Truncamiento
Función de Densidad Condicional: Para modelar datos truncados, necesitamos ajustar la función de densidad para tener en cuenta la exclusión de observaciones fuera del rango permitido. La función de densidad condicional de \(y\) dado que \(y^* > L\) (truncamiento por debajo) es:
\[ f(y) = \frac{f^*(y)}{P(y^* > L)}, \]
donde \(f^*(y)\) es la función de densidad no censurada (o no truncada) de \(y^*\). \(P(y^* > L)\) es la probabilidad de que \(y^*\) sea mayor que \(L\) (es decir, la probabilidad de que la observación no esté truncada).
Probabilidad de Truncamiento: La probabilidad de truncamiento se puede expresar en términos de la función de distribución acumulada (FDA) de \(y^*\): \[ P(y^* > L) = 1 - F^*(L), \] donde \(F^*(L)\) es la F.D.Acumulada de \(y^*\) evaluada en \(L\).
Truncamiento
Verosimilitud
La función de verosimilitud para datos truncados se construye considerando la densidad condicional de las observaciones que no están truncadas. En el caso de truncamiento, la log-verosimilitud incluye solo las observaciones dentro del rango permitido:
\[ \ell(\theta) = \sum_{i: y_i > L} \ln\left(\frac{f^*(y_i | x_i, \theta)}{1 - F^*(L | x_i, \theta)}\right). \]
donde \(\theta\) representa los parámetros del modelo.
Truncamiento
Log-Verosimilitud
Para datos truncados por debajo en \(L\), la función de log-verosimilitud se puede escribir como:
\[ \ell(\theta) = \sum_{i=1}^{n} \left\{ \ln f^*(y_i | x_i; \theta) - \ln \left[1 - F^*(L | x_i; \theta)\right] \right\}\]
donde \(f^*(y_i | x_i; \theta)\) es la densidad condicional de \(y_i^*\) dado \(x_i\) con parámetros \(\theta\). \(F^*(L | x_i; \theta)\) es la función de distribución acumulada (FDA) de \(y_i^*\) evaluada en el umbral \(L\), condicional en \(x_i\).
Notar que la log-verosimilitud se compone de dos términos:
- El primer término, \(\ln f^*(y_i | x_i; \theta)\), es la log-verosimilitud de la variable no truncada \(y_i^*\).
- El segundo término, \(-\ln \left[1 - F^*(L | x_i; \theta)\right]\), ajusta la verosimilitud para tener en cuenta el truncamiento. Representa la probabilidad de observar \(y_i^*\) por encima del umbral \(L\).
- Importancia del Ajuste: Ignorar el truncamiento en los datos implicaría no incluir el segundo término en la log-verosimilitud. Esto resultaría en estimaciones sesgadas e inferencias incorrectas, ya que la muestra truncada no es representativa de la población completa.
Truncamiento
Normalidad (normal truncada)
A menudo se asume que la variable \(y_i^*\) sigue una distribución normal. En este caso, es importante comprender cómo el truncamiento afecta los momentos (media y varianza) de la distribución.
Supongamos que \(z\) sigue una distribución normal \(N(\mu, \sigma^2)\) y que está truncada por debajo en \(L\). La función de densidad de la distribución normal truncada es: \[ f(z | z \geq L) = \frac{f(z)}{1 - \Phi(\alpha)}, \]
donde \(\alpha = \frac{L - \mu}{\sigma}\) (valor estandarizado del umbral de truncamiento) y \(f(z)\) es la densidad normal. \(\Phi(\alpha)\) es la función de distribución acumulada normal estándar.
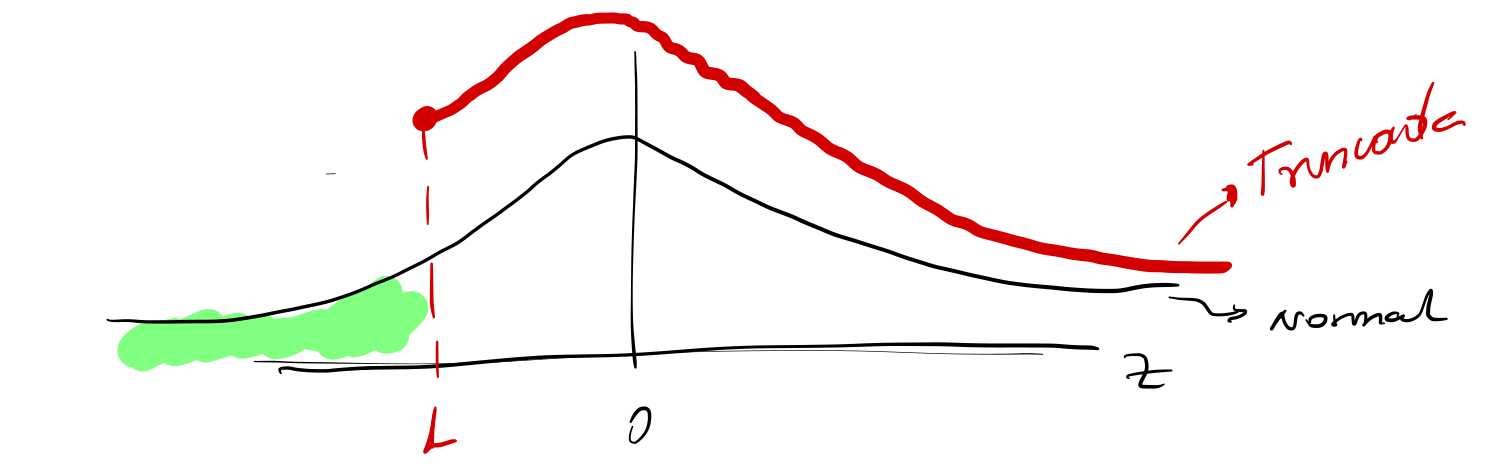
Truncamiento
Distribución Normal Truncada Gráficamente: La densidad normal truncada tiene forma similar a la densidad normal estándar pero restringida al intervalo \([L, \infty)\).
Truncamiento
Normalidad (normal truncada) - Momentos
Media: La media de la distribución normal truncada por debajo en \(L\) es: \[ E(z | z \geq L) = \mu + \sigma \lambda, \]
donde \(\lambda = \frac{\phi(\alpha)}{1 - \Phi(\alpha)}\) es la relación de Mills inversa.
Varianza: La varianza de la distribución normal truncada por debajo en \(L\) es: \[ V(z | z \geq L) = \sigma^2 (1 - \delta), \] donde \(\delta = \lambda (\lambda - \alpha)\) es un factor de ajuste.
Interpretación:
- La relación de Mills inversa (\(\lambda\)) mide el cambio en la media debido al truncamiento.
- El factor de ajuste (\(\delta\)) mide el cambio en la varianza debido al truncamiento.
Truncamiento
Modelo de Regresión Truncada
El modelo de regresión truncada se utiliza cuando la variable dependiente \(y^*\) está truncada, es decir, solo observamos valores de \(y^*\) que caen dentro de un rango determinado.
Estructura del Modelo: Se asume que la variable latente \(y_i^*\) sigue un modelo lineal:
\[ y_i^* = x_i'\beta + \epsilon_i, \quad \epsilon_i \sim N(0, \sigma^2) \]
Truncamiento
Modelo de Regresión Truncada
Distribución de \(y_i^*\) (condicional al truncamiento): La función de densidad de \(y_i^*\) , condicional a que \(y_i^* > L\) (truncamiento por debajo), es:
\[ f^*(y_i | x_i; \theta) = \frac{(1/\sigma) \cdot \phi(\alpha)}{1 - \Phi(\alpha)} \]
donde \(\alpha = \frac{L - x_i'\beta}{\sigma}\).
Probabilidad acumulada hasta el umbral \(L\): \[ F^*(L) = \Phi\left(\frac{L - x_i'\beta}{\sigma}\right) \]
Truncamiento
Modelo de Regresión Truncada
Log-Verosimilitud: La función de log-verosimilitud para el modelo de regresión truncada es:
\[ \ell(\beta, \sigma^2) = \sum_{i=1}^{n} \left[ -\ln(\sqrt{2\pi}\sigma) - \frac{(y_i - x_i'\beta)^2}{2\sigma^2} - \ln\left(1 - \Phi\left(\frac{L - x_i'\beta}{\sigma}\right)\right) \right] \]
Censura, Truncamiento y Modelos de Regresión
Observaciones
- OLS con \(y\) y \(x\) censurados o truncados:
- Inconsistencia: Si aplicamos OLS directamente a datos censurados o truncados, las estimaciones de los coeficientes serán inconsistentes. Esto se debe a que la muestra censurada o truncada no es representativa de la población, lo que introduce un sesgo en las estimaciones.
- Aproximaciones:
- Mínimos Cuadrados Ponderados: Para corregir el sesgo, se pueden utilizar métodos de mínimos cuadrados ponderados, donde las ponderaciones se ajustan para tener en cuenta la censura o el truncamiento. Estos métodos son similares al procedimiento de Heckman para la corrección del sesgo de selección.
- Supuesto de Normalidad:
- En muchos casos, se asume que los errores \(\epsilon_i\) siguen una distribución normal. Este supuesto facilita la derivación de las expresiones para la función de verosimilitud y la estimación de los parámetros.
Censura, Truncamiento y Modelos de Regresión
Medias Condicionales
Media Condicional para Censura por Debajo (umbral \(L = 0\)): \[ E(y | d = 0) = E(y^* | y^* \leq 0) = E(y^*) \cdot P(y^* \leq 0) + E(y^* | y^* > 0). \]
- Interpretación: La media condicional de \(y\) dado que está censurado (\(d=0\)) se puede descomponer en dos términos:
- La media de \(y^*\) (la variable latente) multiplicada por la probabilidad de que \(y^*\) sea menor o igual a cero (la probabilidad de censura).
- La media condicional de \(y^*\) dado que \(y^*\) es mayor que cero (la media de las observaciones no censuradas).
Media Condicional para truncamiento. La media condicional de \(y\) dado \(x\) y que \(y \geq L\) (truncamiento por debajo) es \[ E(y | x, y \geq L) = E(y^* | x, y^* \geq L) = x_i'\beta + \sigma\lambda, \]
donde \(\lambda = \frac{\phi(\alpha)}{1 - \Phi(\alpha)}\) es la relación de Mills inversa.
Censura, Truncamiento y Modelos de Regresión
Fórmulas bajo supuestos de normalidad
Motivación: Cuando asumimos que los errores en el modelo de regresión censurada o truncada siguen una distribución normal, podemos derivar expresiones explícitas para las medias condicionales. Estas expresiones son útiles para comprender el impacto de la censura o el truncamiento en las estimaciones y para desarrollar métodos de corrección.
Censura: Para el modelo de censura por debajo con umbral \(L = 0\), la media condicional de \(\epsilon_i\) dado que \(x_i'\beta + \epsilon_i > 0\) es:
\[ E(\epsilon_i | x_i'\beta + \epsilon_i > 0) = \sigma \cdot \lambda(\alpha), \]
donde \(\alpha = \frac{x_i'\beta}{\sigma}\) es el valor estandarizado de \(x_i'\beta\) y \(\lambda(\alpha) = \frac{\phi(\alpha)}{\Phi(\alpha)}\) es la relación de Mills inversa.
Media Condicional de \(y_i\) (Censura): La media condicional de \(y_i\) dado \(x_i\) y que \(y_i^* > 0\) (no censurado) se puede expresar como:
\[E(y_i | x_i, y_i^* > 0) = \Phi(\alpha) \cdot x_i'\beta + \sigma \cdot \lambda(\alpha)\]
Censura, Truncamiento y Modelos de Regresión
Fórmulas bajo supuestos de normalidad
Truncamiento por debajo (\(L=0\)):
Media Condicional: La media condicional de \(y_i\) dado \(x_i\) y que \(y_i^* \geq 0\) (no truncado) es:
\[ E(y_i | x_i, y_i^* \geq 0) = x_i'\beta + E(\epsilon_i | x_i, \epsilon_i > 0). \]
Bajo normalidad: Asumiendo que \(\epsilon_i \sim N(0, \sigma^2)\), la media condicional se simplifica a:
\[ E(y_i | x_i, y_i^* \geq 0) = x_i'\beta + \sigma \cdot \lambda\left(\frac{x_i'\beta}{\sigma}\right). \]
Censura, Truncamiento y Modelos de Regresión
Estimador de Heckman (en dos pasos)
- El estimador de Heckman, también conocido como el procedimiento de dos pasos de Heckman, se utiliza para corregir el sesgo de selección en modelos de regresión con datos censurados o truncados.
- Este sesgo surge cuando la muestra observada no es representativa de la población, debido a la censura o el truncamiento.
Censura, Truncamiento y Modelos de Regresión
Estimador de Heckman (en dos pasos)
- Primer paso:
- Estimación de la Probabilidad de Selección: Se estima un modelo Probit para la variable indicadora de selección \(d_i\), donde \(d_i = 1\) si \(y_i^* > 0\) (no censurado o no truncado) y \(d_i = 0\) en caso contrario. El modelo Probit se estima utilizando la muestra completa.
- Cálculo de la Relación de Mills Inversa: Se utiliza la estimación del modelo Probit para calcular la relación de Mills inversa \(\hat{\lambda} = \frac{\phi(\hat{\alpha})}{\Phi(\hat{\alpha})}\), donde \(\hat{\alpha} = \frac{x_i'\hat{\beta}}{\hat{\sigma}}\) se obtiene a partir de las estimaciones del Probit.
- Segundo paso:
- Regresión con Corrección de Sesgo: Se estima un modelo OLS de \(y_i\) en \(x_i\) y \(\hat{\lambda}(x_i'\hat{\beta})\), utilizando solo la muestra no censurada o no truncada (\(d_i = 1\)). La inclusión de la relación de Mills inversa como regresor adicional corrige el sesgo de selección.
Censura, Truncamiento y Modelos de Regresión
Estimador de Heckman (en dos pasos)
- Intuición: El primer paso estima la probabilidad de que una observación no esté censurada o truncada. El segundo paso utiliza esta información para ajustar la regresión y corregir el sesgo.
- Corrección de Sesgo: El estimador de Heckman proporciona una forma de obtener estimaciones consistentes de los parámetros del modelo en presencia de censura o truncamiento.
- Matriz de Varianza: Es importante tener en cuenta que la matriz de varianza y los errores estándar deben ajustarse para considerar la estimación en dos pasos. Se utilizan métodos como el método de Murphy-Topel o el bootstrap para obtener errores estándar consistentes.
Truncamiento Incidental o Sesgo de Selección
- Relación con problemas de selectividad en la muestra:
- Se conoce como Sesgo de Selectividad Muestral ( Sample Selectivity Bias ).
- Ocurre cuando la muestra observada no es representativa de la población debido a un proceso de selección no aleatorio.
- Ejemplo: Consideremos el mercado laboral. Una persona entra al mercado laboral si el salario ofrecido es mayor al costo de oportunidad de trabajar. Por ende, una muestra del mercado laboral excluye personas para las cuales no es rentable entrar al mercado.
- Implicaciones:
- Esto genera un problema de sesgo de selección.
- OLS es inconsistente porque el salario observado está correlacionado con la probabilidad de entrar al mercado laboral.
Truncamiento Incidental o Sesgo de Selección
Modelo de Muestra de Selección
Contexto del mercado laboral: Observamos \(y_i\) (salario) solo para las personas que trabajan (\(d_i = 1\)). \(d_i\) es una variable dummy que indica si una persona trabaja, \[ d_i = \begin{cases} 1 & \text{si trabaja} \\ 0 & \text{en caso contrario} \end{cases} \]
Variables Latentes:
- \(y_i^*\): Variable latente de resultado (salario, incluso para los que no trabajan).
- \(d_i^*\): Variable latente que describe la decisión de participar en el mercado laboral.
Definición:
- Si \(d_i^* > 0\): La persona participa en el mercado laboral (\(d_i = 1\)).
- Si \(d_i^* \leq 0\): La persona no participa en el mercado laboral (\(d_i = 0\)).
Truncamiento Incidental o Sesgo de Selección
Modelo de Muestra de Selección. Modelo con Dos Ecuaciones
Para modelar el sesgo de selección, se utiliza un sistema de dos ecuaciones:
Ecuación de Selección: Modela la decisión de participar en el mercado laboral: \[ d_i^* = z_i' \gamma + \epsilon_i, \quad d_i = 1 \text{ si } d_i^* > 0. \]
donde:
- \(z_i\): Vector de variables que influyen en la decisión de participar (e.g., educación, edad, estado civil).
- \(\gamma\): Vector de coeficientes.
- \(\epsilon_i\): Término de error.
Truncamiento Incidental o Sesgo de Selección
Modelo de Muestra de Selección. Modelo con Dos Ecuaciones
Para modelar el sesgo de selección, se utiliza un sistema de dos ecuaciones:
Ecuación de Resultado (outcome): Modela la variable de interés (salario): \[ y_i = x_i' \beta + u_i, \quad \text{observada solo si } d_i = 1. \]
donde:
- \(x_i\): Vector de variables que influyen en el salario (e.g., experiencia, educación).
- \(\beta\): Vector de coeficientes.
- \(u_i\): Término de error.
Ejemplo: \(d_i\) es Participación en el mercado laboral; \(y_i\) es Salario individual; \(z_i\) son características que afectan la participación (ej., nivel educativo); \(x_i\) son características que afectan el salario (e.g., experiencia laboral).
Truncamiento Incidental o Sesgo de Selección
- Selección No Aleatoria: El modelo aborda la selección no aleatoria de la muestra, donde la decisión de participar (o ser observado) está correlacionada con la variable de resultado.
- Correlación de Errores: Los errores \(\epsilon_i\) y \(u_i\) pueden estar correlacionados. Esta correlación es la fuente del sesgo de selección, ya que implica que las variables no observadas que afectan la participación también afectan el resultado.
- Estimación Conjunta: Se requiere una estimación conjunta de las dos ecuaciones para obtener resultados consistentes. El estimador de Heckman (de dos pasos) es un método común para corregir el sesgo de selección en este tipo de modelos.
Truncamiento Incidental o Sesgo de Selección
Modelo Lineal
El truncamiento incidental o sesgo de selección surge cuando la observación de la variable dependiente está condicionada a un proceso de selección. Para modelar este tipo de datos, se utiliza un modelo con dos ecuaciones: una para la selección y otra para el resultado.
Especificación: El modelo de truncamiento incidental se especifica mediante dos ecuaciones lineales:
Ecuación de Participación: \[ y_i^{1*} = x_{i1}' \beta_1 + \epsilon_{i1} \]
Esta ecuación modela la decisión binaria de participar o no en la muestra. La variable latente \(y_i^{1*}\) representa la propensión a participar, y \(x_{i1}\) son las variables que influyen en esta decisión.
Ecuación de Outcome: \[ y_i^{2*} = x_{i2}' \beta_2 + \epsilon_{i2} \]
Esta ecuación modela la variable de resultado \(y_i^{2*}\), que solo se observa si el individuo decide participar (\(y_i^{1*} > 0\)). Las variables \(x_{i2}\) son las que influyen en el resultado.
Relación con el Modelo Tobit: El modelo Tobit es un caso particular de este modelo donde \(y_i^{1*} = y_i^{2*}\), es decir, la variable latente que determina la selección es la misma que la variable de resultado.
Truncamiento Incidental o Sesgo de Selección
Modelo Lineal
Supuesto de Normalidad: Se asume que los errores de ambas ecuaciones, \(\epsilon_{i1}\) y \(\epsilon_{i2}\), siguen una distribución normal bivariada: \[ \begin{pmatrix} \epsilon_{i1} \\ \epsilon_{i2} \end{pmatrix} \sim \mathcal{N} \begin{pmatrix} 0, & \begin{pmatrix} \sigma_1^2 & \rho\sigma_1\sigma_2 \\ \rho\sigma_1\sigma_2 & \sigma_2^2 \end{pmatrix} \end{pmatrix}. \]
Truncamiento Incidental o Sesgo de Selección
Modelo Lineal
Implicaciones:
- \(\rho\): El parámetro \(\rho\) representa la correlación entre los errores de la ecuación de participación y la ecuación de resultado.
- Consistencia: Si \(\rho \neq 0\), existe una correlación entre las variables no observadas que afectan la participación y las que afectan el resultado. Ignorar esta correlación al estimar la ecuación de resultado resultará en estimaciones sesgadas e inconsistentes.
Truncamiento Incidental o Sesgo de Selección
Modelo Lineal
Construcción de la Verosimilitud: Para construir la función de verosimilitud, necesitamos considerar dos casos:
Participación: Si \(y_i^{1*} > 0\), observamos \(y_i^{2*}\). La contribución a la verosimilitud en este caso es la probabilidad conjunta de observar \(y_i^{1*} > 0\) y \(y_i^{2*}\):
\[ P(y_i^{1*} > 0) \cdot f(y_i^{2*} | y_i^{1*} > 0). \]
No Participación: Si \(y_i^{1*} \leq 0\), no observamos \(y_i^{2*}\). La contribución a la verosimilitud en este caso es simplemente la probabilidad de observar \(y_i^{1*} \leq 0\):
\[ P(y_i^{1*} \leq 0). \]
La log-verosimilitud para la muestra completa se obtiene sumando las contribuciones de cada observación, teniendo en cuenta si participa o no en la muestra.
Truncamiento Incidental o Sesgo de Selección
Observaciones
Correlación entre las Ecuaciones: La correlación \(\rho\) entre los errores de las dos ecuaciones captura la dependencia entre la decisión de participar y el resultado. Si \(\rho\) es diferente de cero, es crucial tener en cuenta esta correlación en la estimación.
Modelo de Selección: Este modelo proporciona un marco para incorporar explícitamente la selectividad muestral en el análisis de regresión, permitiendo obtener estimaciones consistentes de los parámetros de interés.
Truncamiento Incidental o Sesgo de Selección
Función de Verosimilitud para el Modelo de Sesgo de Selección
La función de verosimilitud puede escribirse de la siguiente manera:
\[\mathcal{L} = \prod_{i=1}^{N} \left[ P(y_i^{1*} \leq 0) \right]^{1-d_i} \cdot \left[ f(y_i^{2*} | y_i^{1*} > 0) \cdot P(y_i^{1*} > 0) \right]^{d_i}\] donde \(d_i\) es una variable indicadora que toma el valor de 1 si el individuo participa (\(y_i^{1*} > 0\)) y 0 en caso contrario.
La función de verosimilitud es el producto de las probabilidades de observar cada individuo en la muestra. Para los individuos que no participan (\(d_i = 0\)), la probabilidad es simplemente \(P(y_i^{1*} \leq 0)\). Para los individuos que participan (\(d_i = 1\)), la probabilidad es la probabilidad conjunta de observar \(y_i^{1*} > 0\) y \(y_i^{2*}\).
Truncamiento Incidental o Sesgo de Selección
Supuesto de Normalidad. Asunción Clave: Para simplificar la función de verosimilitud, se asume que los errores \(\epsilon_{i1}\) y \(\epsilon_{i2}\) tienen una distribución conjunta bivariada normal estándar:
\[ \begin{pmatrix} \epsilon_{i1} \\ \epsilon_{i2} \end{pmatrix} \sim \mathcal{N} \begin{pmatrix} 0, & \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix} \end{pmatrix}. \]
Probabilidad de Participación: Bajo este supuesto, la probabilidad de participación se puede expresar como:
\[P(y_i^{1*} > 0) = \Phi\left( \frac{x_{i1}'\beta_1}{\sqrt{1-\rho^2}} \right)\]
donde \(\Phi(\cdot)\) es la función de distribución acumulada de la normal estándar.
Truncamiento Incidental o Sesgo de Selección
Bajo el supuesto de normalidad, la log-verosimilitud para este modelo está dada por:
\[\ell(\beta_1, \beta_2, \rho) = \sum_{y_i = 0} \ln\left( \Phi\left( \frac{x_{i1}'\beta_1}{\sqrt{1-\rho^2}} \right) \right) + \sum_{y_i = 1} \ln\left( \phi\left( \frac{y_i^{2*} - x_{i2}'\beta_2}{\sqrt{1-\rho^2}} \right) \cdot \Phi\left( \frac{x_{i1}'\beta_1 + \rho \frac{y_i^{2*} - x_{i2}'\beta_2}{\sqrt{1-\rho^2}}}{\sqrt{1-\rho^2}} \right) \right). \]
donde \(\phi(\cdot)\) es la función de densidad de la normal estándar.
Truncamiento Incidental o Sesgo de Selección
Alternativa a la Máxima Verosimilitud: El método de Heckman en dos pasos es una alternativa a la estimación por máxima verosimilitud. Es computacionalmente menos costoso, pero requiere el supuesto de normalidad de los errores.
Pasos:
Relación entre los Errores: Bajo el supuesto de normalidad bivariada, la relación entre los errores de las dos ecuaciones se puede escribir como: \[ \epsilon_{i2} = \rho \epsilon_{i1} + \xi_i, \]
donde \(\xi_i\) es independiente de \(\epsilon_{i1}\) y \(\xi_i \sim \mathcal{N}(0, \sigma^2_\xi)\).
Media Condicional: La media condicional del outcome (\(y_i^{2*}\)) dado que el individuo participa (\(y_i^{1*} > 0\)) es: \[ \mathbb{E}(y_i^{2*} | y_i^{1*} > 0) = x_{i2}'\beta_2 + \rho \lambda(x_{i1}'\beta_1), \]
donde \(\lambda(\cdot)\) es el Inverse Mills Ratio \(\lambda(x) = \frac{\phi(x)}{\Phi(x)}\).
Corrección del Sesgo: El término \(\rho \lambda(x_{i1}'\beta_1)\) corrige el sesgo de selección. La relación de Mills inversa (\(\lambda(x)\)) captura la información sobre la selección no aleatoria de la muestra.
Truncamiento Incidental o Sesgo de Selección
Método de Heckman en Dos Pasos (Heckit):
El método de Heckman, también conocido como Heckit, es un procedimiento en dos pasos que se utiliza para corregir el sesgo de selección en modelos de regresión. Este método es una alternativa a la estimación por máxima verosimilitud completa y es especialmente útil cuando se asume una distribución normal bivariada para los errores.
Pasos:
- Probit para la Participación:
Se estima un modelo probit para la variable indicadora de participación \(d_i\), donde \(d_i = 1\) si el individuo participa (\(y_i^{1*} > 0\)) y \(d_i = 0\) en caso contrario.
La probabilidad de participación se modela como: \[ P(d_i = 1 | x_{i1}) = \Phi(x_{i1}'\beta_1), \]
donde \(\Phi(\cdot)\) es la función de distribución acumulada de la normal estándar.
Se obtienen las estimaciones de los coeficientes \(\hat{\beta}_1\) del modelo probit.
Se calcula la relación de Mills inversa (\(\lambda\)) para cada individuo utilizando las estimaciones del probit: \[ \hat{\lambda}_i = \lambda(x_{i1}'\hat{\beta}_1) = \frac{\phi(x_{i1}'\hat{\beta}_1)}{\Phi(x_{i1}'\hat{\beta}_1)}, \]
Truncamiento Incidental o Sesgo de Selección
Método de Heckman en Dos Pasos (Heckit):
Pasos:
- Regresión OLS Aumentada:
Se estima la ecuación de resultado (\(y_i^{2*}\)) mediante una regresión OLS que incluye la relación de Mills inversa (\(\hat{\lambda}_i\)) como una variable explicativa adicional:
\[ y_i^{2*} = x_{i2}'\beta_2 + \rho \sigma_2 \hat{\lambda}_i + \nu_i, \]
donde \(\rho\) es la correlación entre los errores de las dos ecuaciones y \(\sigma_2\) es la desviación estándar del error en la ecuación de resultado.
La inclusión de \(\hat{\lambda}_i\) corrige el sesgo de selección.
Truncamiento Incidental o Sesgo de Selección
Método de Heckman en Dos Pasos (Heckit):
Ventajas del Método Heckit:
- Simplicidad: Es fácil de implementar, ya que solo requiere la estimación de un modelo probit y una regresión OLS.
- Amplitud: Es aplicable a una amplia variedad de modelos de selección, como el análisis del mercado laboral, la participación en programas sociales y las decisiones de inversión.
- Supuestos: Requiere menos supuestos que la máxima verosimilitud completa, pero asume la normalidad conjunta de los errores \(\epsilon_{i1}\) y \(\epsilon_{i2}\).
Prueba de Hipótesis:
- Se puede realizar una prueba de hipótesis para determinar si la correlación entre los errores (\(\rho\)) es significativamente diferente de cero: \(H_0: \rho = 0\).
- Si se rechaza la hipótesis nula (\(H_0\)), se recomienda utilizar la máxima verosimilitud completa (MLE) en lugar de OLS, ya que OLS no captura adecuadamente el sesgo de selección cuando \(\rho \neq 0\).
Comparación de Métodos: Es recomendable comparar los resultados del método de Heckman (Heckit) con los de la máxima verosimilitud completa (MLE) en un ejemplo práctico. Esto ayuda a comprender las diferencias entre los métodos y el impacto del sesgo de selección en las estimaciones.
Clarificación de Conceptos: La comparación de los métodos también puede ayudar a clarificar las diferencias entre selección, censura y truncamiento, y a comprender cómo cada uno de estos problemas afecta la estimación de los modelos de regresión.
Nota: Siempre es importante entender los supuestos y limitaciones de cada método para seleccionar el más adecuado en contextos prácticos.
Truncamiento Incidental Ejemplo en Stata (heckman)
* 1. Simular datos
clear all
set seed 123
set obs 1000
gen x1 = rnormal(0, 1)
gen x2 = rnormal(0, 1)
gen z = rnormal(0, 1)
matrix C = (1, 0.5 \ 0.5, 1)/*Para errores correlacionados*/
drawnorm e1 e2, corr(C)
* Sim. ecuación de selección (participación)
gen y1s = 0.5*x1 + 0.3*z + e1 /*y1s es la variable latente*/
gen y1 = (y1star > 0)
* Sim. ecuación de outcome (para participantes)
gen y2 = 0.8*x2 - 0.2*z + e2
replace y2 = . if y1 == 0
* Paso 1: Probit para la participación
probit y1 x1 z
predict xb, xb
gen lambda = normalden(xb)/normal(xb) /*inv. mills ratio*/
* Paso 2: OLS con corrección del sesgo de selección
reg y2 x2 z lambda if y1 == 1 /*se eliminan missings*/
* Comparación ahora con comando de Stata:
heckman y2star x2 z, select(y1 = x1 z) two
heckman y2star x2 z, select(y1 = x1 z) /* mle */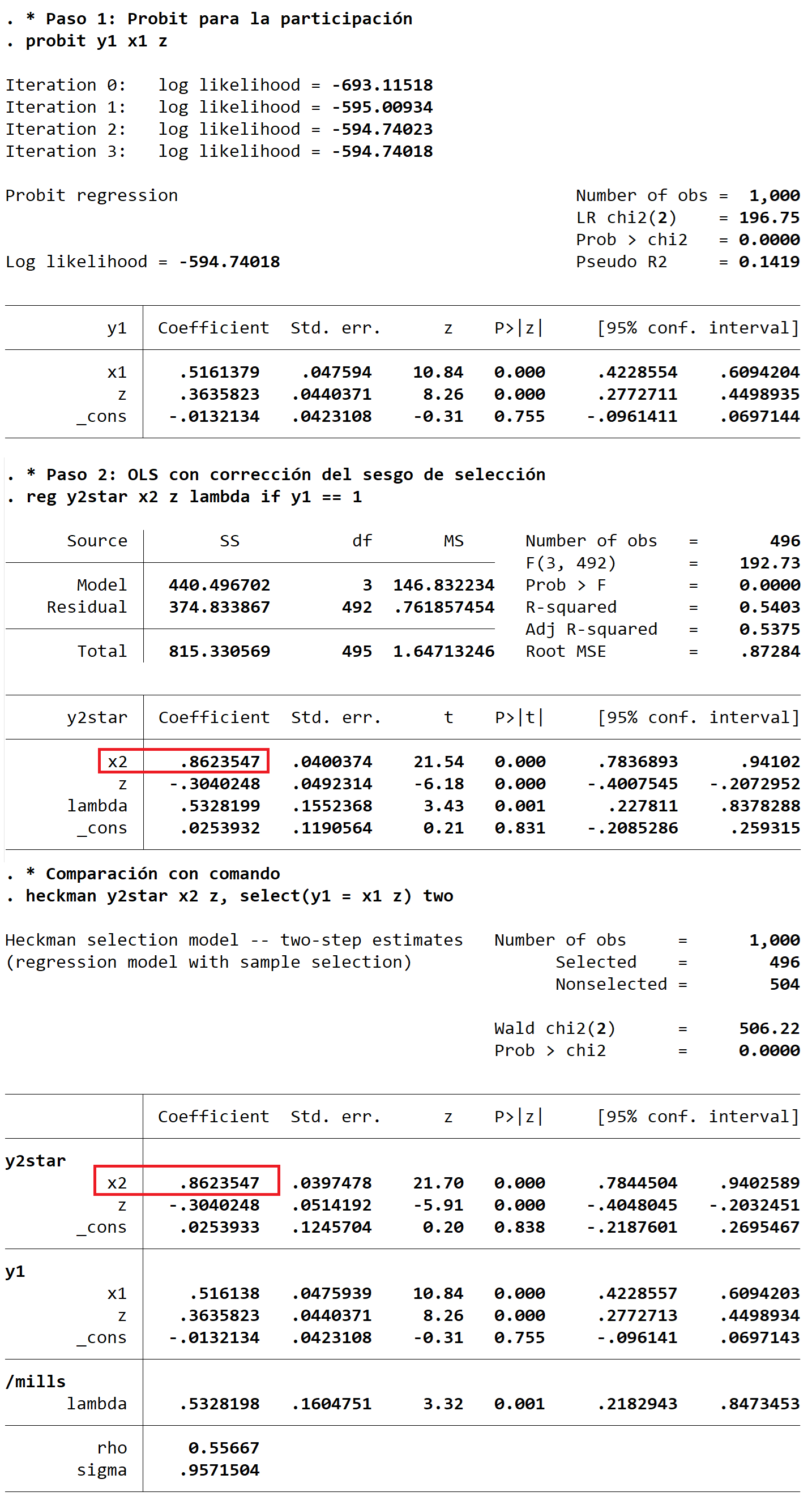
Cierre
¿Preguntas?

