Oferta y Demanda
(Fundamentos) Microeconomía
Contenidos
- Oferta y Demanda
- Mercado y Equilibrio
- Elasticidad
- Equilibrio, alteraciones en las condiciones de mercado, intervención del gobierno
1. Oferta y Demanda
Oferta y Demanda
Oferta
La curva de oferta: Representa la relación entre la cantidad ( \(Q\) ) de un bien a la cual los productores están dispuestos a vender, dado el precio final del bien o servicio ( \(P\) ).
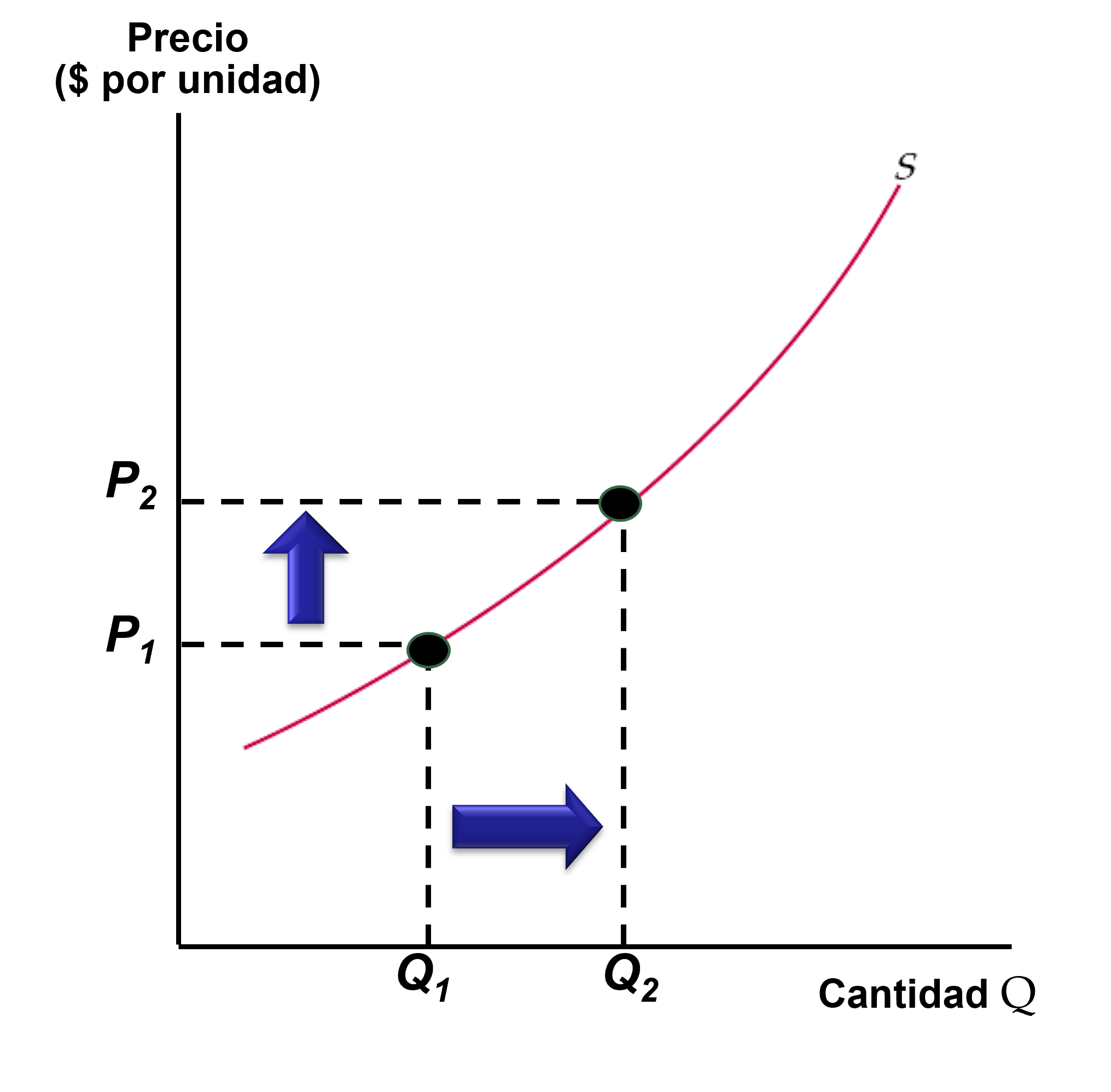
Figura: Curva de Oferta
- La curva de oferta muestra como la cantidad de un bien o servicio ofertado para venta cambia a medida que cambian los precios.
- La curva de oferta tiene pendiente positiva (creciente): A mayor precio ( \(\uparrow P\) ), más firmas o empresas se encuentran dispuestas a vender y producir ( \(\uparrow Q^s\) ):
\[\boldsymbol{Q^s=Q^s(\underbrace{P}_{ \color{red}{(+)} })}\] Por ejemplo, \(Q^s=1,5+0,25\cdot P\)
Nota: La ‘s’ corresponde a nomenclatura anglo. ( supply )
Oferta y Demanda
Oferta
Cambios en la curva de oferta:
Variaciones o cambios en el precio se reflejan a trav'es de movimientos en la curva de oferta.
Variaciones o cambios en algunas otras variables que afectan producci'on (diferentes al precio) conllevan a desplazamientos en la curva de oferta. En particular, variables que afecten los costos de producción:
Mano de obra (salarios)
Capital (tasa de interés que se paga)
Costos asociados a materias primas
Cuando el costo de producción baja o se reduce ( \(\downarrow Costos\) ), el producto de la empresa aumenta ( \(\uparrow Q^s\) ), lo cual se representa con un desplazamiento hacia la derecha de la curva de oferta.
Oferta y Demanda
Oferta
Cambios en la curva de oferta
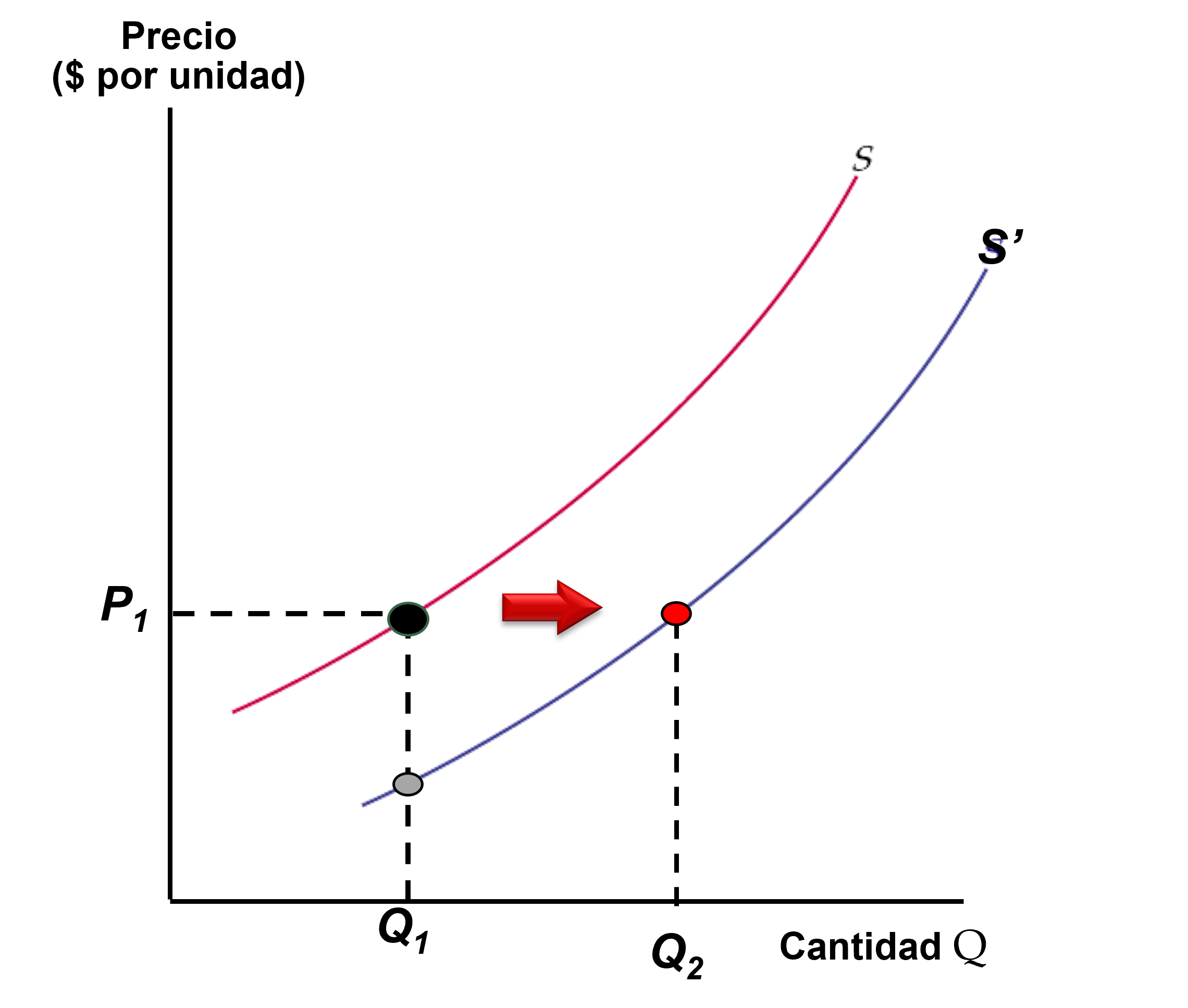
Figura: Desplazamientos de la Oferta
Si el costo de producción cae ( \(\downarrow Costos\) ), las empresas pueden
- producir la misma cantidad a un precio menor
- producir mayor cantidad si mantienen el precio (como en la figura)
En cualquier caso, la curva se desplaza (desde S a S’ ).
Oferta y Demanda
Demanda
La curva de demanda: Representa la relación entre la cantidad ( \(Q^d\) ) de un bien o servicio a la cual los consumidores están dispuestos a comprar, dado el precio final del bien o servicio ( \(P\) ).
Figura: Curva de demanda
- La curva de demanda muestra como la cantidad de un bien o servicio consumido cambia a medida que cambian los precios.
- La curva de demanda tiene pendiente negativa (decreciente): A mayor precio \(\uparrow P\) , menos agentes se encuentran dispuestos a adquirir el bien o servicio \(\downarrow Q^d\) :
\[\boldsymbol{Q^d=Q^d(\underbrace{P}_{ \color{red}{(-)} })}\] Por ejemplo, \(Q^d=3-0,5\cdot P\)

Oferta y Demanda
Demanda
Cambios en la curva de demanda: Variaciones o cambios en el precio se reflejan a través de movimientos a lo largo de la curva de demanda. Sin embargo, cambios en otras variables que determinen las decisiones de compra de los consumidores (diferentes al precio del bien o servicio) podrían conllevar a desplazamientos en la curva de demanda.
Algunas de las (potenciales) fuentes son: Cambios en el ingreso, cambios en las preferencias, o cambios en los precios de otros bienes o servicios.
- Bienes sustitutos Un incremento en el precio de uno lleva a un incremento de la cantidad demandada del otro. Ejemplo: papas (pure) y arroz.
- Bienes complementarios Un incremento en el precio de uno produce una reducción en la cantidad demandada del otro. Ejemplo: Cereal y leche.
Oferta y Demanda
Demanda
Cambios en la curva de demanda
Figura: Desplazamientos de la Demanda
En general, la cantidad demandada sube cuando sube el ingreso de los hogares.
Un ingreso más alto permite acceder a más bienes, por lo que (bajo condiciones normales) se representa con un desplazamiento de la curva de demanda hacia la derecha (desde D a D’) como muestra la figura.

2. Mercado y Equilibrio
Mercado y Equilibrio
● Equilibrio: Es el precio \(P^*\) para el cual la cantidad demandada se iguala a la cantidad ofertada, es decir, se vacía el mercado.
En equilibrio la oferta y demanda se igualan
\[\boldsymbol{Q^*=Q^s(P^*)=Q^d(P^*)}\]
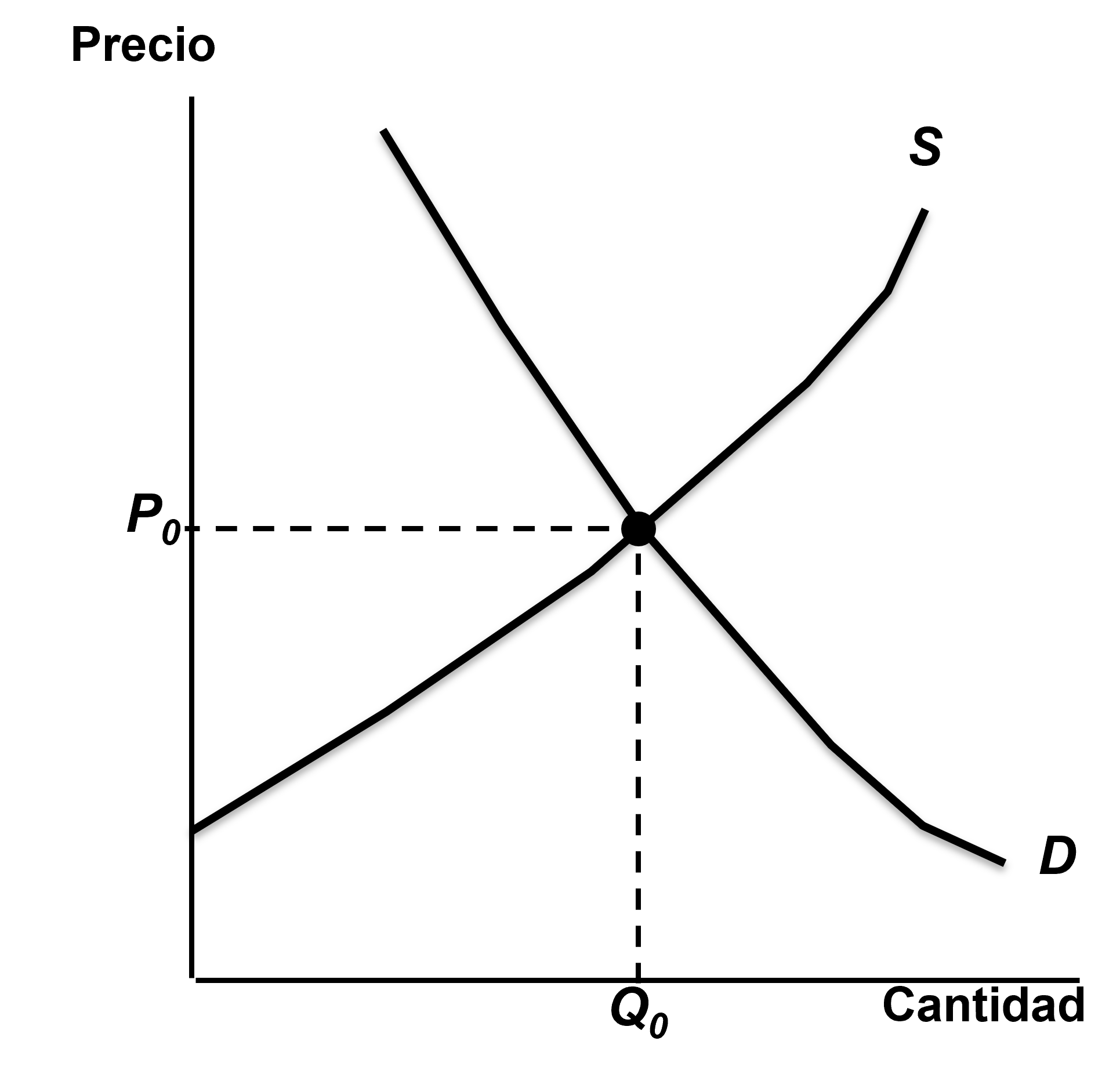
En la figura se representa con el punto de intersección de las dos curvas.
Por ejemplo, para \(Q^d=3-0,5\cdot P\) y \(Q^s=1,5+0,25\cdot P\), al igualar las dos ecuaciones y despejar para \(P\), se obtiene: \(P^*=2\) y \(Q^*=2\).
Nota: El ’*’ significa cantidades y precios en equilibrio.
Mercado y Equilibrio
El mecanismo de mercado hace referencia a la tendencia en un precio (de libre mercado) a cambiar hasta que el mercado se vacía.
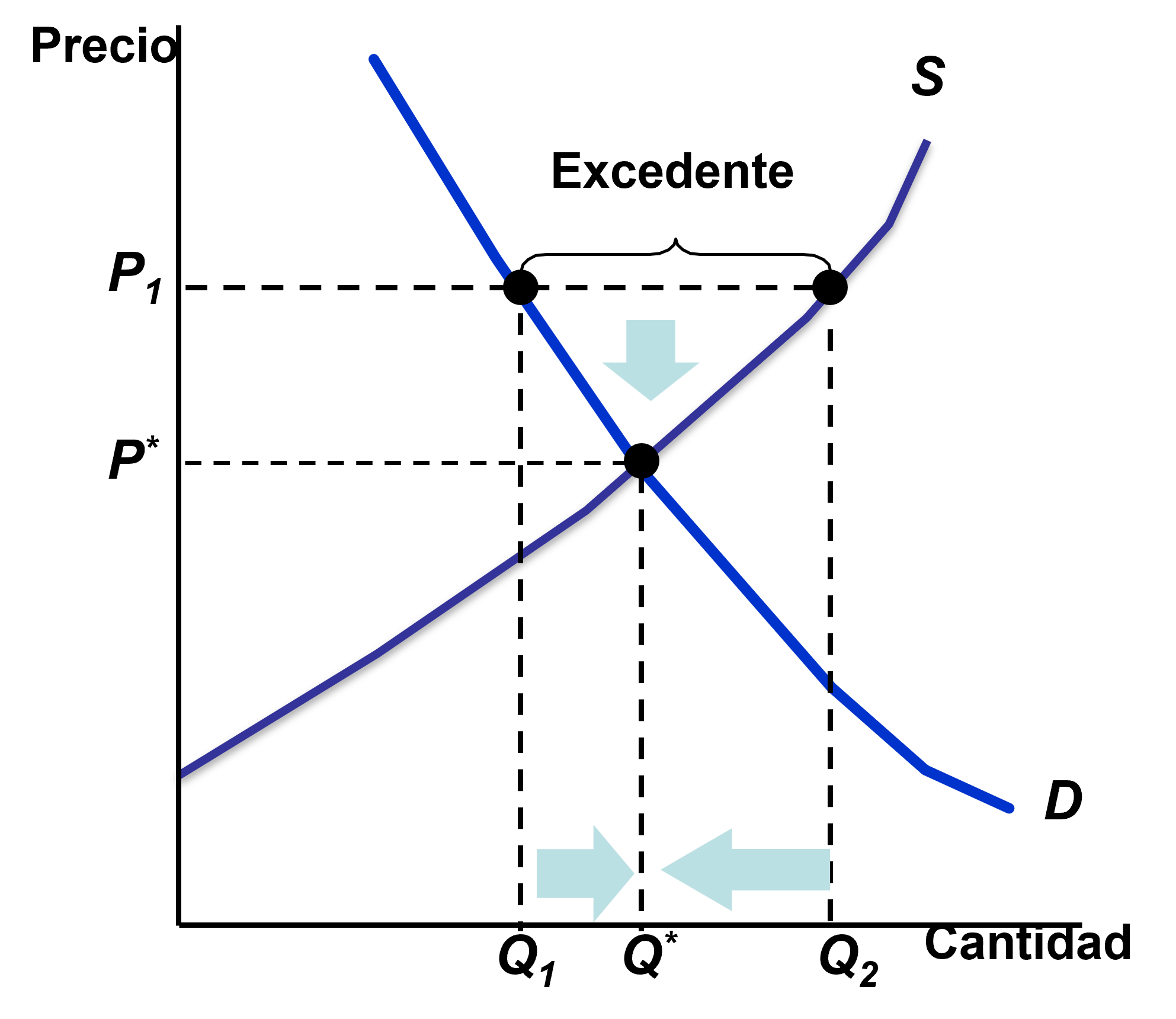
Figura: Excedente en el mercado.
Excedente: \(Q^s>Q^d\)
Si el precio se encuentra por encima de \(P^*\) (es decir, el precio está por encima del precio que vacía el mercado):
- Se genera excedente. Es decir, la cantidad ofertada supera la demandada.
- Dado el exceso de oferta, los productores empiezan a bajar los precios y la cantidad demandada empieza aumentar.
- Así, el mercado continúa ajustándose hasta alcanzar el precio de equilibrio(hasta llegar al precio que vacía el mercado).
Mercado y Equilibrio
Por ahora, un supuesto fundamental para estos ajustes es que el mercado es al menos competitivo.
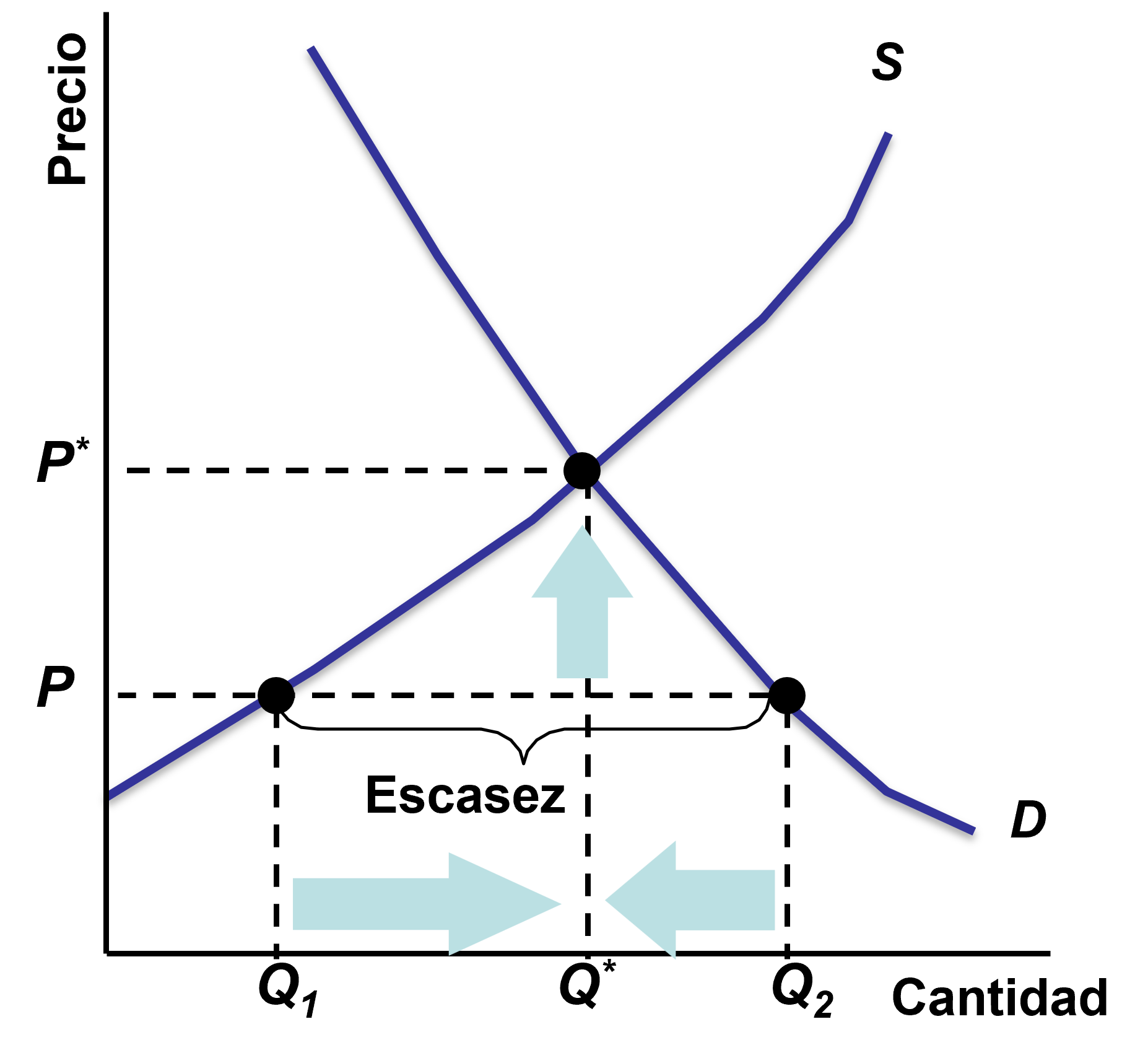
Figura: Escasez en el mercado.
Escasez: \(Q^d>Q^s\)
Si el precio se encuentra por debajo de \(P^*\) (es decir, el precio está por debajo del precio que vacía el mercado):
- Se genera escasez. Es decir, la cantidad demandada supera la oferta.
- Dado el exceso de demanda, los productores empiezan a subir los precios y la cantidad demandada empieza a disminuir y la ofertada aumenta.
- Así, el mercado continúa ajustándose hasta alcanzar el precio de equilibrio (hasta llegar al precio que vacía el mercado).
Mercado y Equilibrio
Desplazamientos de las Curvas y Equilibrio
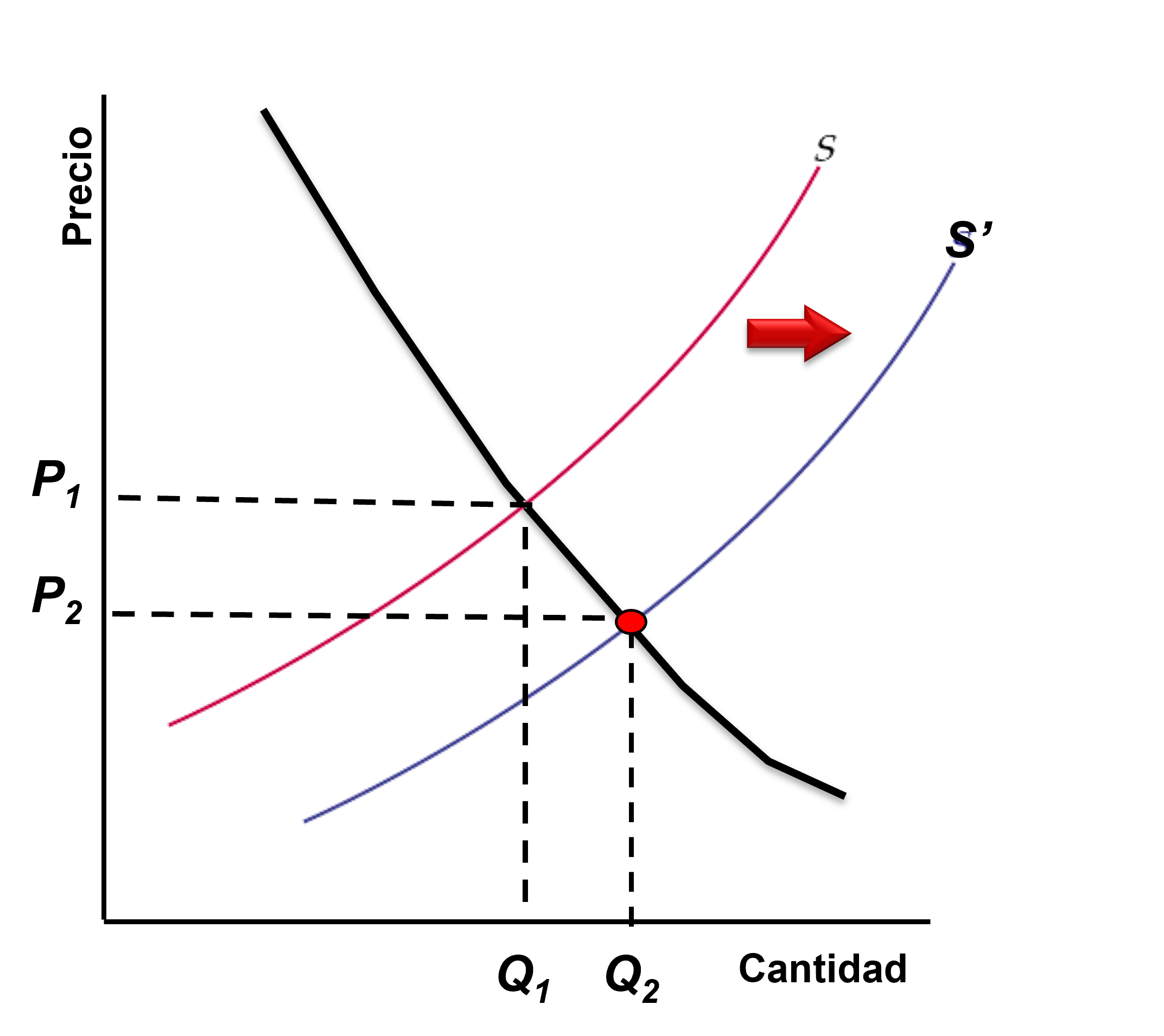
Figura: Variaciones en la oferta.
Cuando la curva de oferta se desplaza a la derecha, el mercado se vacía a un precio más bajo y una mayor cantidad. Es decir, \(\downarrow P\) y \(\uparrow Q\).
Nuevamente, el aumento en la oferta puede estar asociado, por ejemplo, a una reducción en el costo de los insumos.
Mercado y Equilibrio
Desplazamientos de las Curvas y Equilibrio
Figura: Variaciones en la demanda
Cuando la curva de demanda se desplaza a la derecha, el mercado se vacía a un precio más alto y una mayor cantidad. Es decir, \(\uparrow P\) y \(\uparrow Q\).
Nuevamente, el desplazamiento en la curva puede estar, por ejemplo, asociado a un aumento del ingreso (para un bien o servicio normal).

Mercado y Equilibrio
Desplazamientos de las Curvas y Equilibrio
Es de resaltar que el resultado final de las variaciones en el equilibrio, en términos de cuánto crecerá o no el precio o la cantidad, dependerá de la pendiente de las curvas y de cuánto cambie la curva. Veamos, por ejemplo, el caso del desplazamiento de la oferta a modo de ilustración. Si la demanda es más plana (lado izquierdo), se tendrá mayor variación en la cantidad.
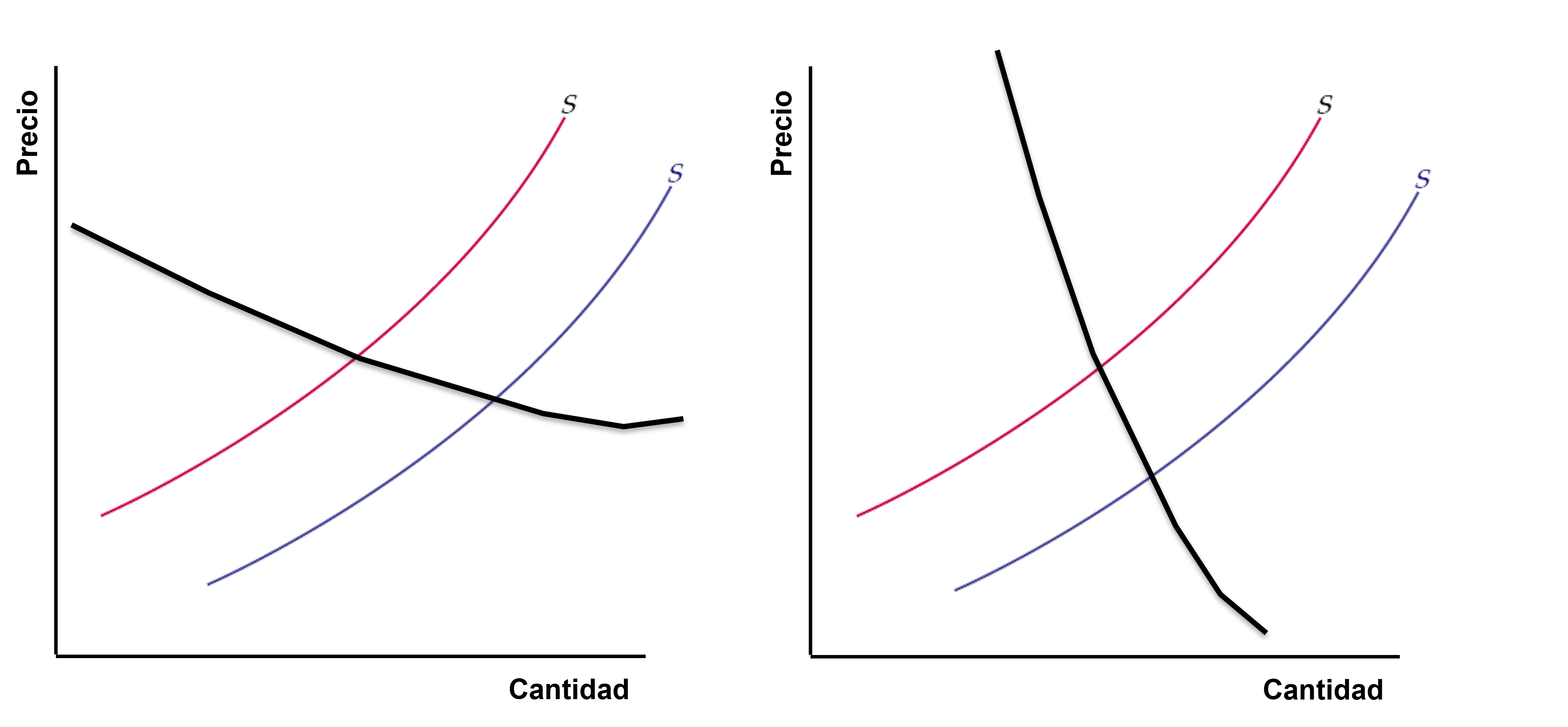
Nota: El concepto relacionado es elasticidad. Un tema que abordaremos más adelante.
Mercado y Equilibrio
Desplazamientos de las Curvas y Equilibrio
¿Cuál sería el resultado si cambian ambas curvas a la vez? La respuesta sería: depende
Figura: Variaciones en la oferta y demanda
El resultado sobre el precio y la cantidad de equilibrio está determinado por:
- El tamaño relativo y la dirección del cambio
- La pendiente de las curvas
En el ejemplo particular presentado en la figura, al desplazar a la derecha la oferta y la demanda, el precio y la cantidad incrementan.

3. Elasticidad
Elasticidad
- En la discusión de los desplazamientos de las curvas resalté la importancia de las pendientes y usé la palabra elasticidad.
- Por ejemplo, la pendiente de la curva de demanda en el plano \((Q,P)\) está definida por \((\Delta Q^d / \Delta P)^{-1}<0\). Esto corresponde al inverso de la disminución que sufre la cantidad demandada (por ejemplo, en 2Kg) al subir los precios (por ejemplo, en $1 por Kg).
- Es decir, la variación está asociada a las unidades en que se miden la cantidad de bienes o servicios (por ejemplo, Kg) y su precio (por ejemplo, $/Kg).
- Existe otra forma más general de cuantificar dichos cambios y es la elasticidad. La elasticidad deja a un lado el uso de unidades particulares de medida (por ejemplo, Kg) y emplea porcentajes.
La elasticidad es una medida porcentual del cambio en una variable ( \(Y\) ) que resulta de un uno porciento de incremento en otra variable ( \(X\) ). Es decir,
\[\boldsymbol{\xi_{x,y}=\Delta\%Y/\Delta\%X}\]
Nota: El porcentaje de cambio se puede determinar de la siguiente forma: \(\Delta\%Y=(\Delta Y/Y)*100=100*(\text{Valor Final de Y}-\text{Valor Inicial de Y})/\text{Valor Inicial de Y}\).
Elasticidad
Elasticidad Precio de la Demanda \(\xi_{p,d}\)
La elasticidad precio de la demanda es el porcentaje en el que cambia la cantidad demandada de un bien o servicio como resultado de un incremento del 1-porciento en el precio del bien o servicio:
\[\xi_{p,d}=\frac{\Delta\%Q^d}{\Delta\%P}=\frac{(\Delta Q^d/Q^d)\cdot100}{(\Delta P/P)\cdot100}=\boldsymbol{\frac{\Delta Q^d}{\Delta P}\frac{P}{Q^d}}\]
Elasticidad
Elasticidad Precio de la Demanda \(\xi_{p,d}\)
Ejemplo. Supona que a un precio inicial de $200 por kg de pan la cantidad que se demanda es de 12 Kilos. Al subir el precio a $250 la cantidad que se demanda (cae y ) pasa a ser de 8 Kg.
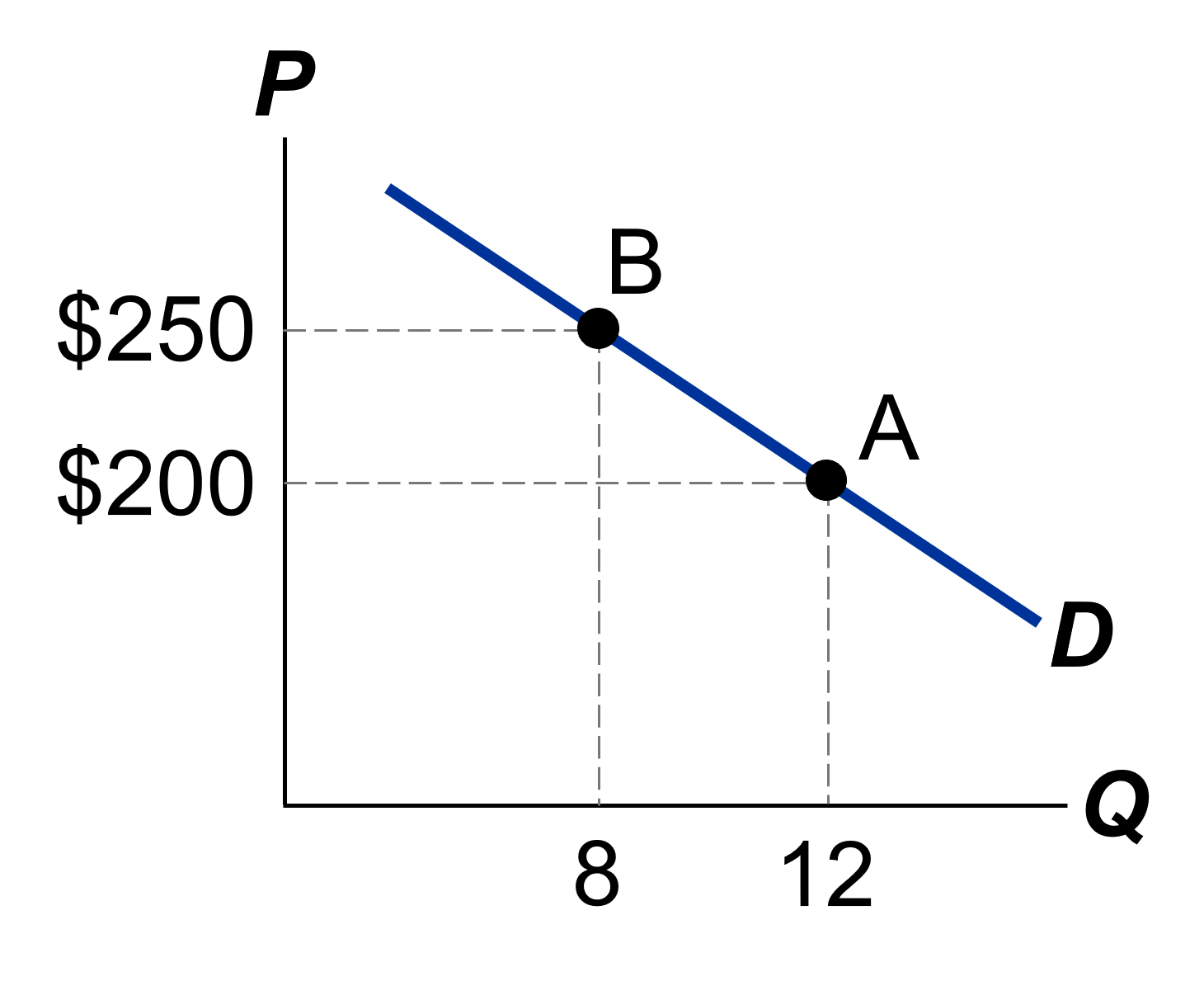
Primero determinamos las variaciones porcentuales
- Porcentaje de cambio en P es ( $250 – $200)/$200 * 100 = 25%
- Porcentaje de cambio en Q es ( 8 – 12)/12 * 100 = - 33%
Por ende, la elasticidad precio de la demanda es 33/25=1.33
Nota: Se tiende a omitir el signo negativo al hablar de la elasticidad precio de la demanda ya que se entiende que al subir el precio cae la cantidad demandada.
Elasticidad
Elasticidad Precio de la Demanda
En una curva de demanda lineal como la del ejemplo, \(Q^d=3−0,5\cdot P\), la elasticidad cambia a lo largo de la recta:
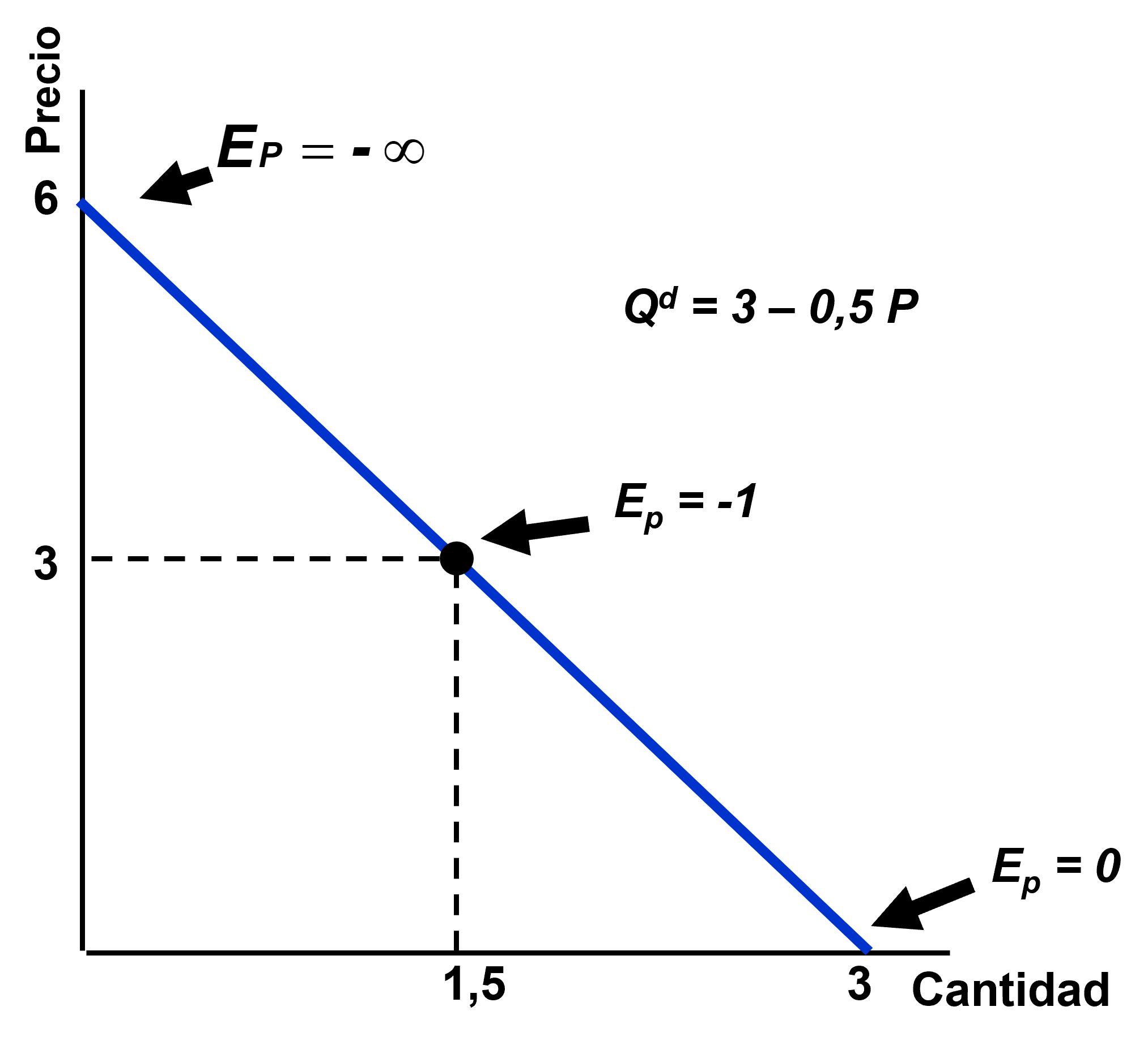
Elasticidad
Elasticidad Precio de la Demanda \(\xi_{p,d}\)
Interpretación de los valores obtenidos para la elasticidad precio de la demanda:
Demanda elástica
- El precio elasticidad de la demanda > 1
Demanda inelástica
- El precio elasticidad de la demanda < 1
Demanda de elasticidad unitaria
- El precio elasticidad de la demanda = 1
Elasticidad
Elasticidad Precio de la Demanda
Ejemplo. Comparemos (de forma intuitiva) la idea de elasticidad para diferentes bienes. Responder la encuesta accediendo al código QR o al enlace forms.office.com/r/GfmGmH4EbU

Elasticidad
Elasticidad Precio de la Demanda
Análisis de respuestas
Caso 1: Cereal para el desayuno vs. Protector Solar (¿Si el precio de ambos bienes se incrementa en 20%, para cuál de los dos bienes cae más la demanda?)
- El cereal para el desayuno tiene más sustitutos cercanos, por lo tanto los compradores pueden cambiar de opción facilmente si el precio del cereal incrementa.
- El protector solar no tiene sustitutos cercanos, por lo tanto, ante un incremento de precio, la demanda no se vería muy afectada.
Conclusión:
La elasticidad-precio de la demanda es mayor cuando hay sustitutos cercanos disponibles.
Elasticidad
Elasticidad Precio de la Demanda
Análisis de respuestas
Caso 2: Insulina vs. Yates (El precio de ambos bienes se incrementa en 20%, para cuál de los bienes cae más la demanda? Por qué?)
- La insulina es una necesidad para los diabéticos. Un incremento en su precio causará un pequeño o quizás ninguna reducción en la demanda.
- Un yate, es un bien de lujo, un incremento en su precio causará que algunas personas decidan no comprarlo.
Conclusión:
La elasticidad-precio de la demanda es más alta para los bienes de lujo que para los bienes de primera necesidad.
Elasticidad
Elasticidad Precio de la Demanda
Análisis de respuestas
Caso 3: Jeans vs. Ropa (El precio de ambos bienes se incrementa en 20%, para cuál de los bienes cae más la demanda?)
- En una definición estricta, para blue jeans hay muchos sustitutos.
- Hay pocos sustitutos disponibles para bienes ampliamente definidos como ropa.
Conclusión:
La elasticidad-precio de la demanda es más alta para los bienes definidos de forma estricta (específica) que para los definidos de forma amplia.
Elasticidad
Elasticidad Precio de la Demanda
Análisis de respuestas
Caso 2: Insulina vs. Yates (El precio de ambos bienes se incrementa en 20%, para cuál de los bienes cae más la demanda? Por qué?)
- La insulina es una necesidad para los diabéticos. Un incremento en su precio causará un pequeño o quizás ninguna reducción en la demanda.
- Un yate, es un bien de lujo, un incremento en su precio causará que algunas personas decidan no comprarlo.
Conclusión:
La elasticidad-precio de la demanda es más alta para los bienes de lujo que para los bienes de primera necesidad.
Elasticidad
Elasticidad Precio de la Demanda
El horizonte temporal también es importante
Caso extra: Gasolina o bencina en el corto plazo vs. largo plazo (El precio de la bencina se incrementa en 20%, la cantidad demandad cae más en el corto o en largo plazo? Por qué?)
- En el corto plazo, no es mucho lo que los consumidores pueden hacer, más allá de tomar bus/metro, usar bicicletas, etc.
- En el largo plazo, los consumidores pueden elegir comprar un auto híbrido o más económico en bencina, mudarse más cerca del trabajo, etc.
Conclusión:
La elasticidad precio es mayor en el largo plazo para la bencina.
Elasticidad
Elasticidad Precio de la Demanda
El horizonte temporal también es importante
Caso extra: Autos en el corto plazo vs. largo plazo
En el caso de la demanda de autos ocurre lo contrario. Si el precio sube, los consumidores posponen inicialmente la compra de un nuevo auto, por lo que la cantidad demandada anual desciende significativamente.
En el largo plazo, los autos más viejos se desgastan y hay que reponerlos, por lo que la cantidad anual demandada se recupera. Por lo tanto, la demanda es menos elástica a largo plazo que a corto plazo.
Conclusión:
La elasticidad precio es menor en el largo plazo para los autos.
Elasticidad
Elasticidad Precio de la Demanda
Otras Elasticidades de la Demanda
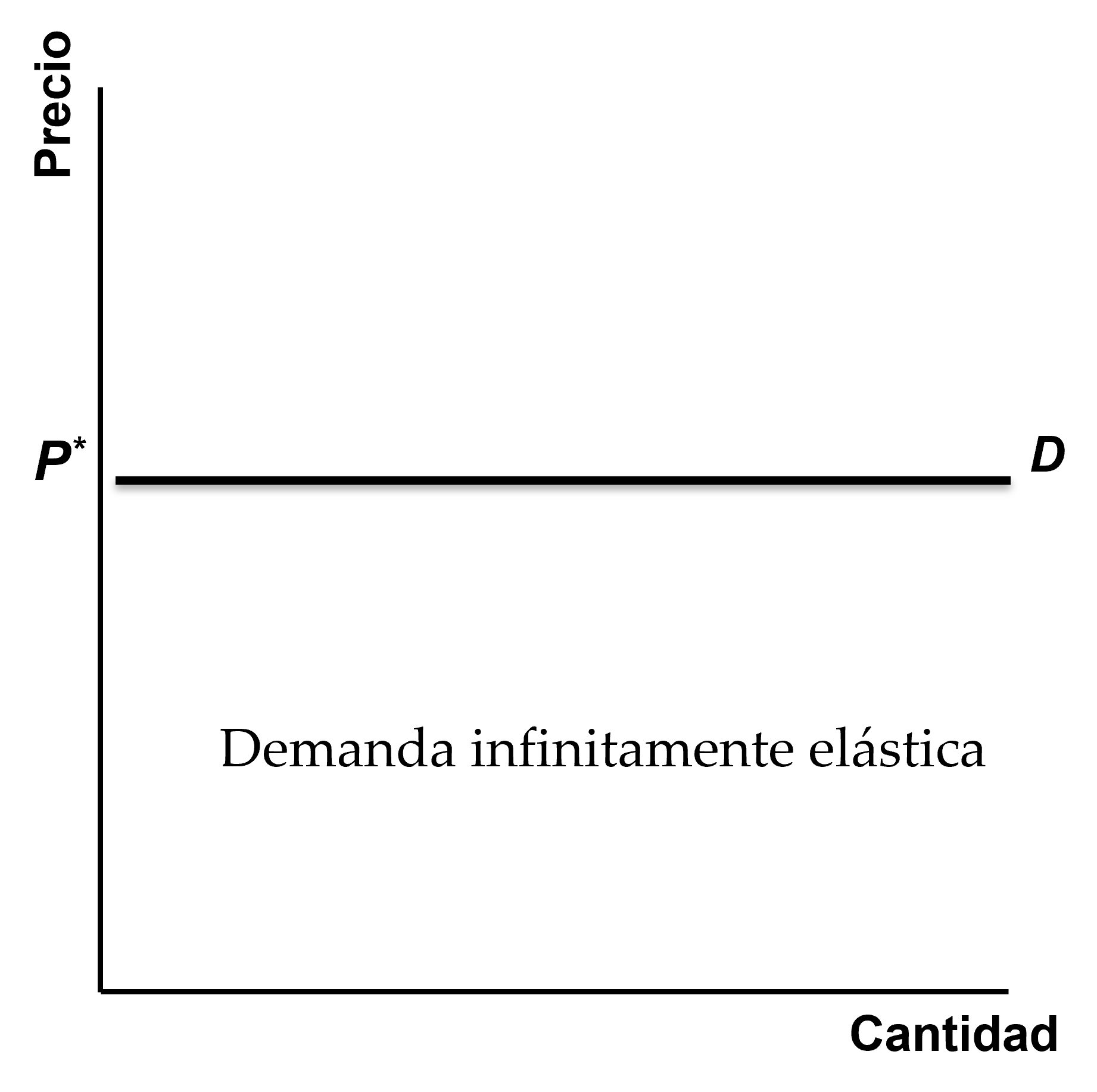
Figura: Demanda infinitamente elástica
En el caso de una curva horizontal, la demanda es infinitamente elástica
- \(\Delta Q/ \Delta P\rightarrow\infty\). Es decir, una pequeña variación en el precio provoca una enorme variación en la demanda.
- Elasticidad infinita ( \(\xi_{p,d}=\infty\) ) : Los consumidores comprarán todo lo que puedan a un único precio P* , pero a cualquier precio mayor a éste ( P>P* ), la cantidad demanda desciende a cero.
- Mientras que a cualquier descenso del precio, la demanda aumenta ilimitadamente.
Elasticidad
Elasticidad Precio de la Demanda
Otras Elasticidades de la Demanda
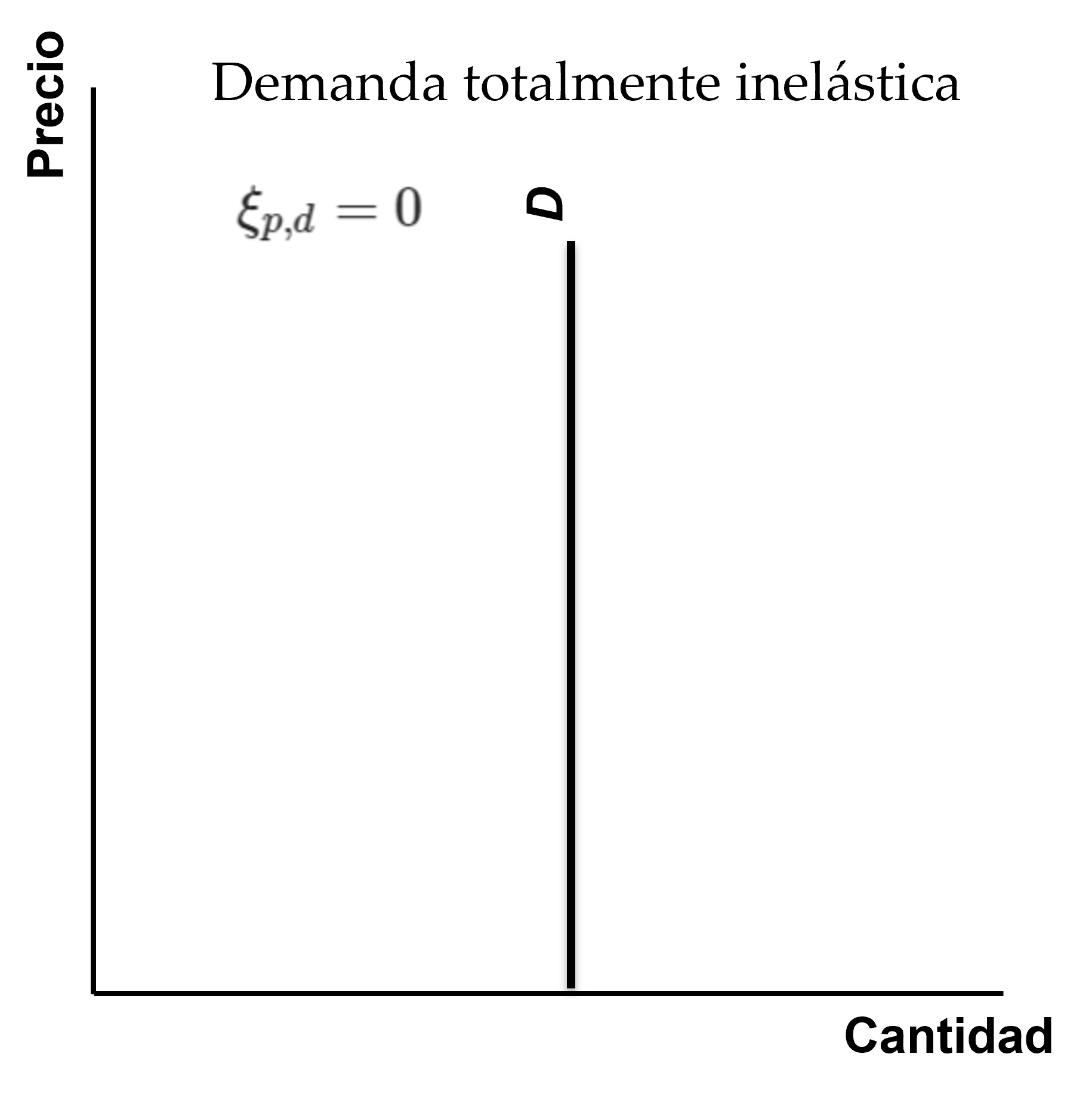
Figura: Demanda inelástica
En el caso de una curva vertical, la demanda es inelástica
- \(\Delta Q/ \Delta P\rightarrow 0\). Es decir, una variación en el precio no provoca una variación en la demanda.
- Elasticidad cero ( \(\xi_{p,d}=0\) ) : Como la cantidad demanda es la misma a cualquiera que sea el precio, la elasticidad de demanda es cero.
- Los consumidores compran una cantidad fija Q*, cualquiera que sea el precio.
Elasticidad
Otras Elasticidades
Con lo visto hasta ahora es trivial extender el concepto de elasticidad a otra combinación de variables. Verémos a continuación:
- La elasticidad arco (o punto medio) de la demanda
- Elasticidad-renta de la demanda
- Elasticidad-precio cruzada de la demanda
- Elasticidad precio de la oferta
Elasticidad
Elasticidad arco o punto medio de la demanda
Antes de entrar en ecuaciones formales, veamos la intuición de la elasticidad arco empleando un ejemplo familiar.

Anteriormente encontramos que al movernos del punto A al B la elasticidad era
- Porcentaje de cambio en P es \(( \$250 – \$200)/ \color{blue}{\$200} * 100 = 25\%\)
- Porcentaje de cambio en Q es \(( 8 – 12)/\color{blue}{12} * 100 = - 33\%\)
- 33/25=1.33
Pero, si hacemos el computo iniciando del punto B hacia el A:
- Porcentaje de cambio en P es \(( \$200 – \$250)/ \color{blue}{\$250} * 100 = -20\%\)
- Porcentaje de cambio en Q es \(( 12 – 8)/\color{blue}{8} * 100 = 50\%\)
- 50/20=2.5
Es decir, para los mismos dos puntos, ¡se obtiene un valor diferente!
Elasticidad
Elasticidad arco o punto medio de la demanda
En el ejemplo anterior, la controversia se genera por el punto tomado como punto inicial (A vs B, resaltados en color azul).
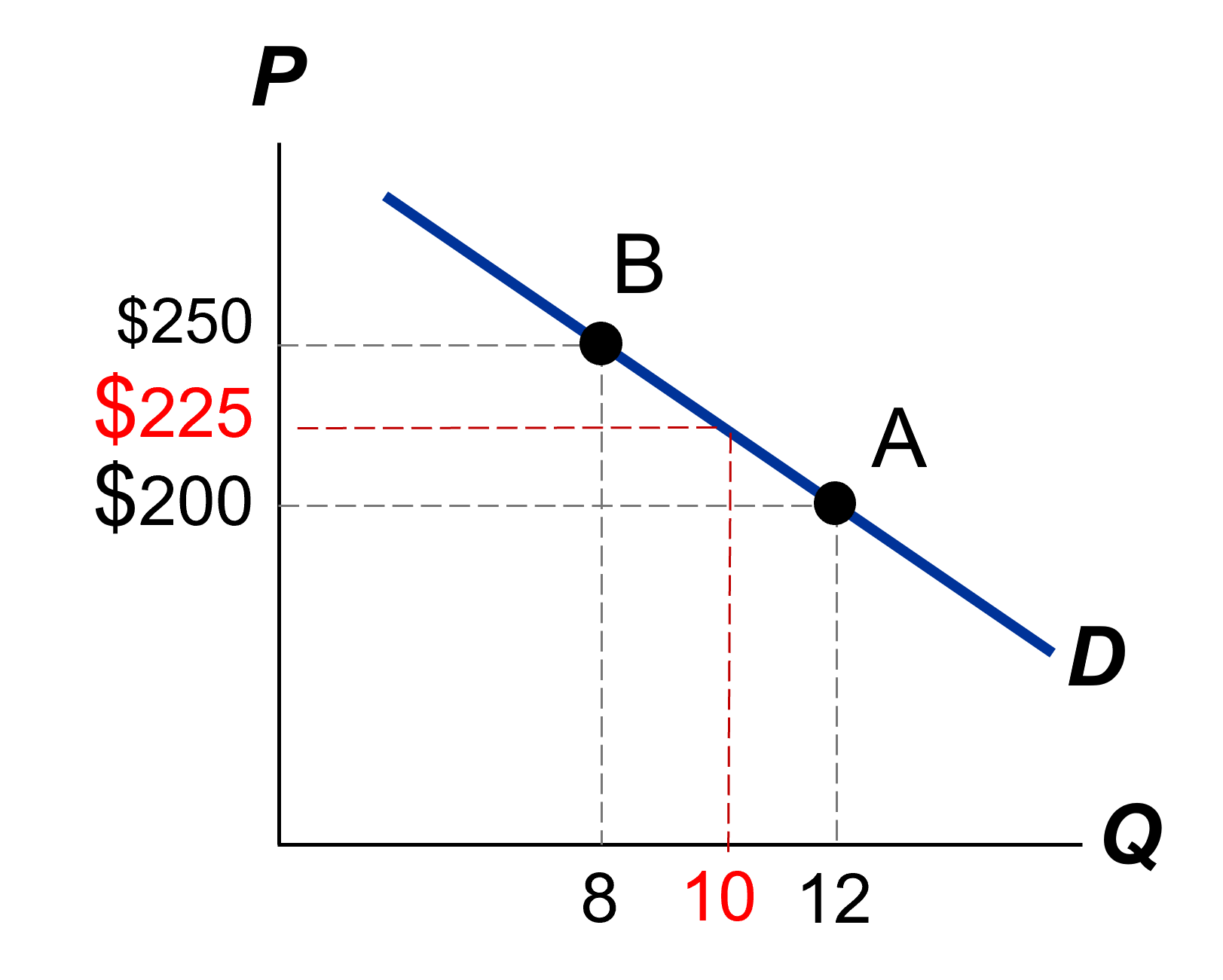
Un solución sencilla sería que al dividir en el computo de las tasas de variación se use el punto medio:
- Porcentaje de cambio en P es \(( \$250 – \$200)/ \color{red}{\$225} * 100 = 22\%\)
- Porcentaje de cambio en Q es \(( 8 – 12)/\color{red}{10} * 100 = -40\%\)
Esta es la idea detrás de la elasticidad arco o punto medio.
Elasticidad
Elasticidad arco o punto medio de la demanda
- Formalmente, el punto medio de los precios es \(\bar{P}=(P_1+P_2)/2\) y el de las cantidades es \(\bar{Q}=(Q_1+Q_2)/2\).
- Por ende, \[Elasticidad=\frac{\Delta Q/\bar{Q}}{\Delta P/\bar{P}}=\frac{(Q_2-Q_1)/(Q_2+Q_1)}{(P_2-P_1)/(P_2+P_1)}\]
- Ejemplo. Para el ejemplo anterior, sería: \[Elasticidad=\frac{(8-12)/10}{(250-200)/225}=\frac{40}{22}=1,8\]
Elasticidad
Elasticidad renta de la demanda
La Elasticidad-renta de la demanda es la variación porcentual que experimenta la cantidad demandada cuando la renta \(I\) aumenta un 1 por ciento: \[\xi_{I,d}=\frac{\Delta Q}{\Delta I}\frac{I}{Q}\]
- Las elasticidades-renta a corto plazo también son diferentes de las elasticiadades rentas a largo plazo.
- De la mayoría de los bienes y servicios –alimentos, bebidas, combustibles, actividades recreativas, etc.- la elasticidad-renta de la demanda es mayor en el largo plazo que en el corto plazo.
- En el caso de los bienes duraderos, ocurre lo contrario. En el corto plazo, la elasticidad-renta de la demanda es mucho mayor que la elasticiadad a largo plazo.
Elasticidad
Elasticidad-precio cruzada de la demanda
La Elasticidad-precio cruzada de la demanda es la variación porcentual que experimenta la cantidad demanda de un bien (‘a’) cuando sube el precio un 1 por ciento el precio de otro (‘b’):
\[\xi_{Q_a,P_b}=\frac{\Delta Q_a}{\Delta P_b}\frac{P_b}{Q_a}\] Ejemplo. Si el precio del arroz sube un 10% y la cantidad demandada de papas sube un 20%, la elasticidad precio cruzada de la demanda de papas es +2. En este caso, el signo aporta información respecto a si son bienes complementarios o sustitutos.
Elasticidad
Elasticidad precio de la oferta
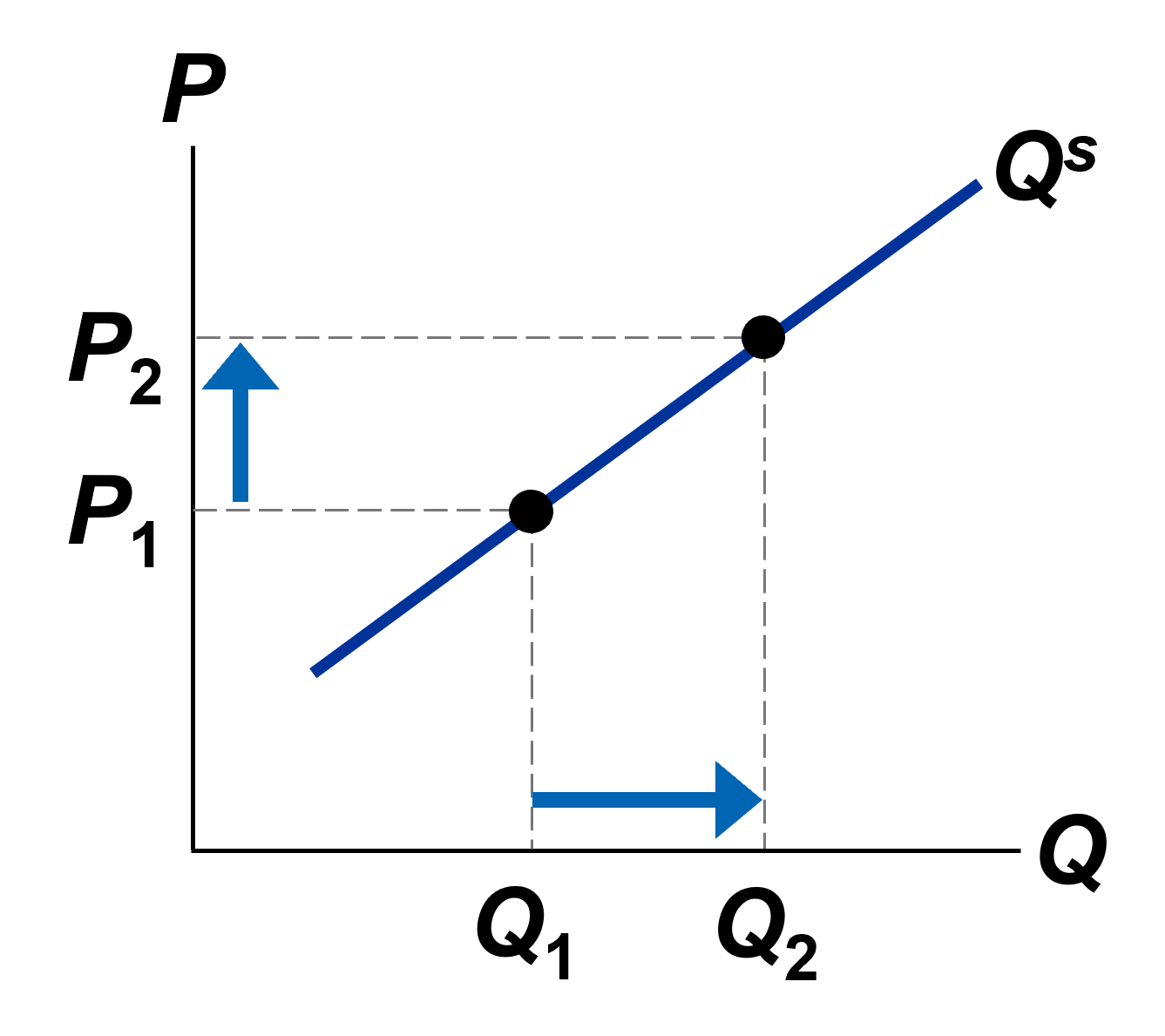
La Elasticidad precio de la oferta es la variación porcentual que experimenta la cantidad ofrecida de un bien cuando el precio sube un 1 por ciento.
\[\xi_{p,s}=\frac{\Delta Q^s}{\Delta P}\frac{P}{Q^s}\] Ejemplo. Si P se incrementa en 8%, \(Q^s\) se incrementa en 16%. Por ende, \(\xi_{p,s}=16/8=2\)
Elasticidad
Elasticidad precio de la oferta
Mayor o menor elasticidad de la oferta: determinantes
- Cuanto más fácilmente los vendedores puedan cambiar la cantidad que producen, mayor es la elasticidad precio de la oferta.
- Ejemplo: La oferta de propiedades en Viña del Mar cerca del Casino es más difícil de variar y, por lo tanto, menos elástica que la oferta de, por ejemplo, los automóviles nuevos.
- La elasticidad precio de la oferta es mayor a largo plazo que a corto plazo para algunos bienes. Es decir, la curva de oferta exhibe mayor pendiente en el corto plazo.
- A largo plazo, las empresas pueden construir nuevas fábricas o pueden ingresar al mercado nuevas empresas.
- Ejemplo: La producción de cobre. Si sube el precio, a las empresas les gustaría producir más, pero tienen limitaciones de capacidad a corto plazo. En el largo plazo, pueden aumentar la capacidad y producir más.
4. Equilibrio, alteraciones en las condiciones de mercado, intervención del gobierno
Políticas del Gobierno y Mercado
Cuando revisamos los principios de economía (Mankiw), se citó un corolario a la idea de Smith: Cuando un gobierno impide que los precios se ajusten, se dificulta la capacidad de la mano invisible para coordinar.
Estudiaremo ahora cómo algunas políticas de gobierno pueden alterar el resultado del mercado.
En particular, revisaremos los siguientes temas:
- Control de precios
- Precio tope o máximo (sobre el precio al que se puede vender un bien)
- Precio mínimo (legal sobre el cual se puede vender un bien)
- Impuestos:
- El gobierno puede hacer que los compradores / vendedores paguen una cantidad específica por cada unidad.
- Control de precios
Políticas del Gobierno y Mercado
Control de precios: Precio tope o máximo.
- El gobierno puede imponer un precio tope ya sea por encima o por debajo del precio que se obtendría en un mercado competitivo.
- Por ejemplo, supongamos que el gobierno considera que los arriendos de departamentos están muy altos en Santiago e impone un tope.
- Este precio tope puede tener o puede no tener efectos (vinculante).
Políticas del Gobierno y Mercado
Control de precios: Precio tope o máximo.
Figura: Precio Tope NO vinculante.
Un precio máximo por encima del precio de equilibrio NO es vinculante. Es decir, no tiene ningún efecto sobre el resultado del mercado.

Políticas del Gobierno y Mercado
Control de precios: Precio tope o máximo.
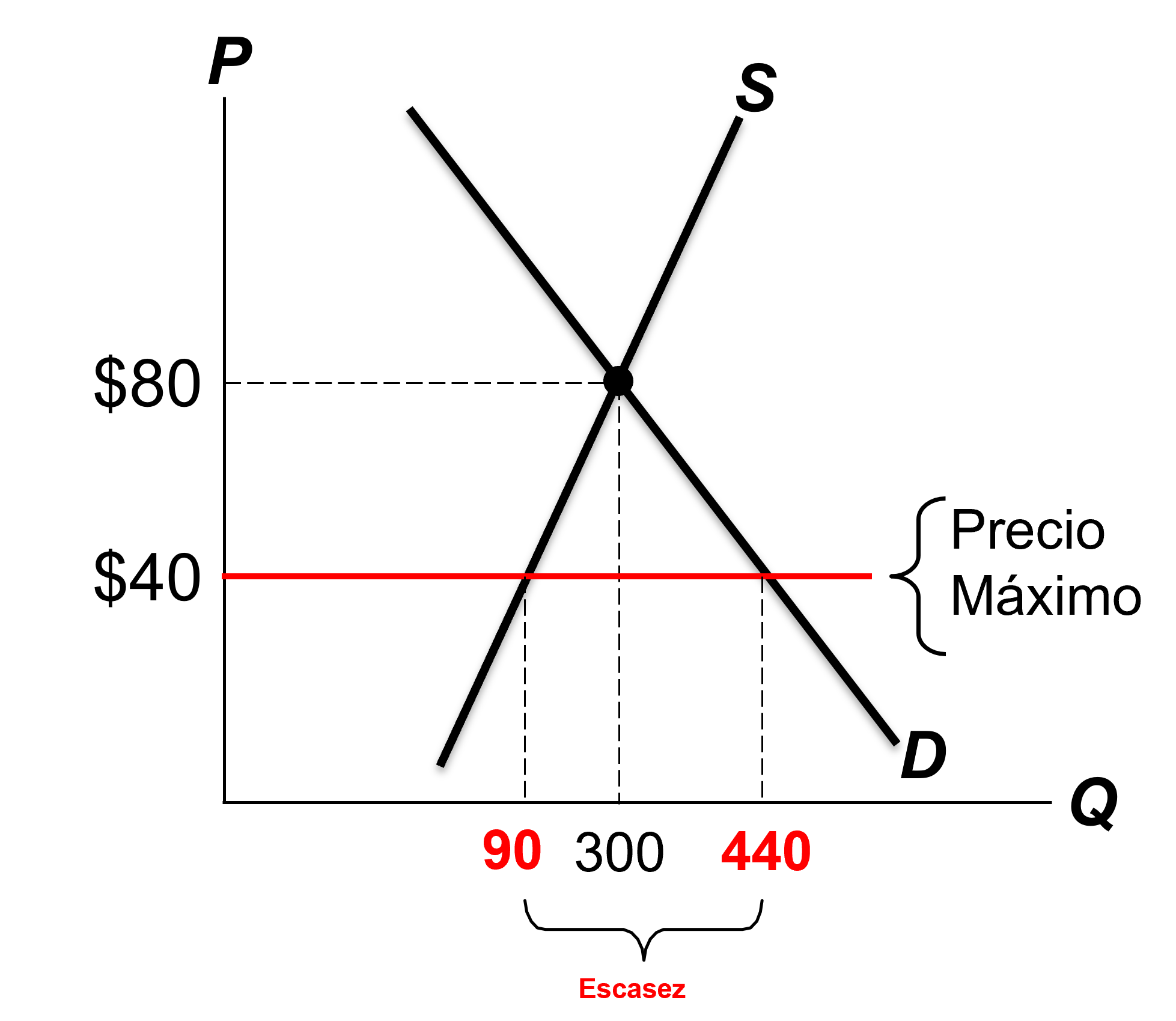
Figura: Precio Tope vinculante.
Un precio máximo por debajo del precio de equilibrio SÍ es vinculante. Es decir, tiene efecto sobre el resultado del mercado.
Políticas del Gobierno y Mercado
Control de precios: Precio Mínimo
- El gobierno impone un precio mínimo por el cual se pueda vender algo. Por ejemplo, la mano de obra (salario mínimo).
Figura: Precio Mínimo NO vinculante.
Un precio mínimo por debajo del precio de equilibrio NO es vinculante. Es decir, no tiene ningún efecto sobre el resultado del mercado.

Políticas del Gobierno y Mercado
Control de precios: Precio Mínimo
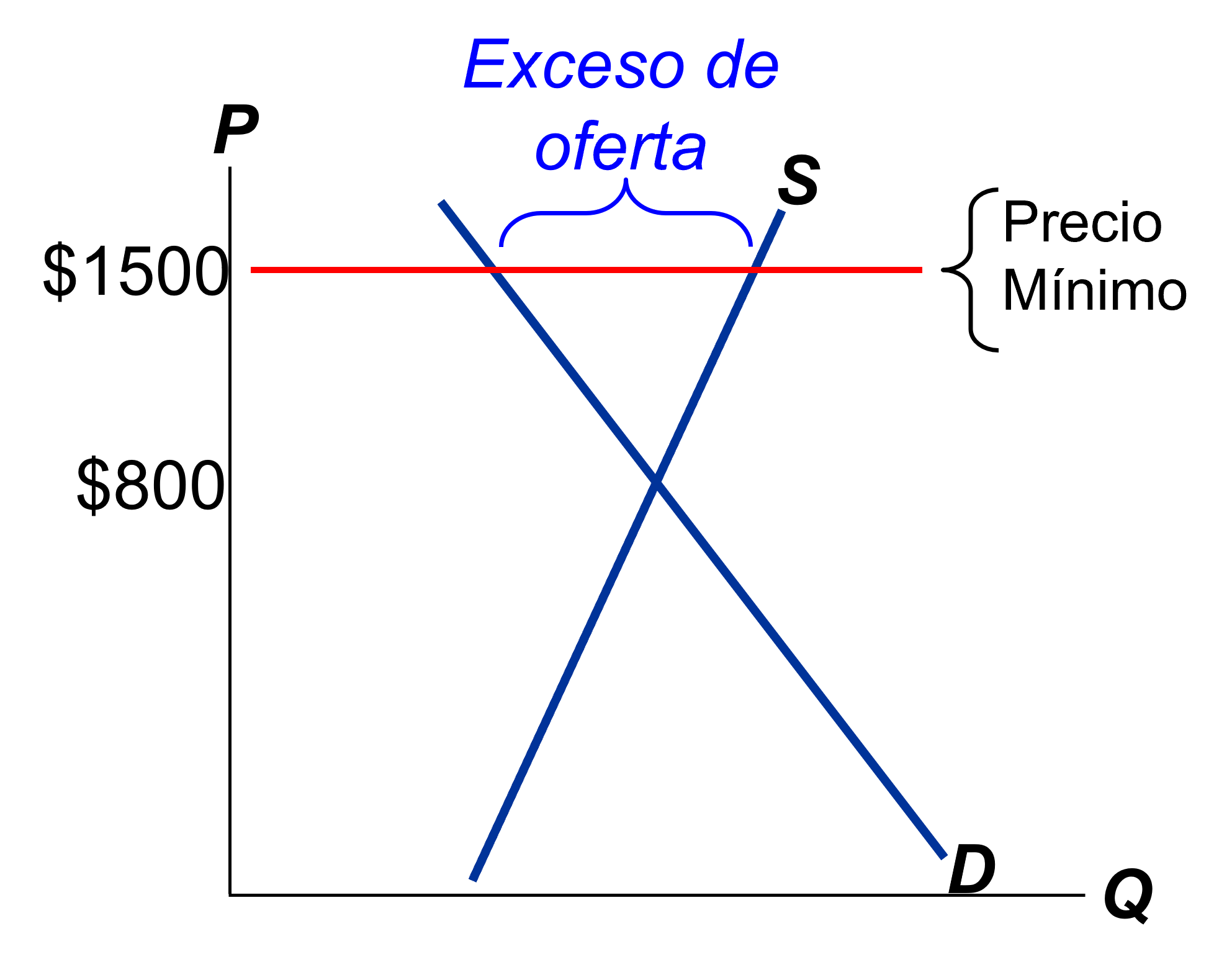
Figura: Precio mínimo vinculante.
Un precio mínimo por encima del precio de equilibrio SÍ es vinculante. Es decir, tiene efecto sobre el resultado del mercado.
Políticas del Gobierno y Mercado
Impuestos
El gobierno usa impuestos con el fin de recaudar ingresos para proyectos públicos (educación, salud, defensa nacional, etc.) Leyes de controles de renta o alquileres.
Un tema relevante en la incorporación de un impuesto al mercado es la Incidencia Fiscal (forma en la que la carga de un impuesto se comparte entre los participantes en un mercado).
El gobierno puede obligar al vendedor o al comprador a pagar el impuesto.
Como veremos a continuación, desde el punto de vista de la recaudación del gobierno, da igual si el impuesto se colecta sobre el comprador o el vendedor.
Políticas del Gobierno y Mercado
Impuestos
Ejemplo. Supongamos un mercado cuyo precio y cantidad de equilibrio (sin impuestos) son $10 y 500, respectivamente.
Figura: Equilibrio sin impuestos.
Primero revisaremos el caso en el cual el gobierno impone un impuesto de $1,5 por unidad a los consumidores. Es decir, sobre la curva de demanda.
Luego revisaremos el caso en el cual el gobierno impone un impuesto de $1,5 por unidad a los productores. Es decir, sobre la curva de oferta.

Políticas del Gobierno y Mercado
Impuestos
Ejemplo. Parte 1: El gobierno impone un impuesto a los consumidores.
(i) Desplazamiento de la curva de demanda
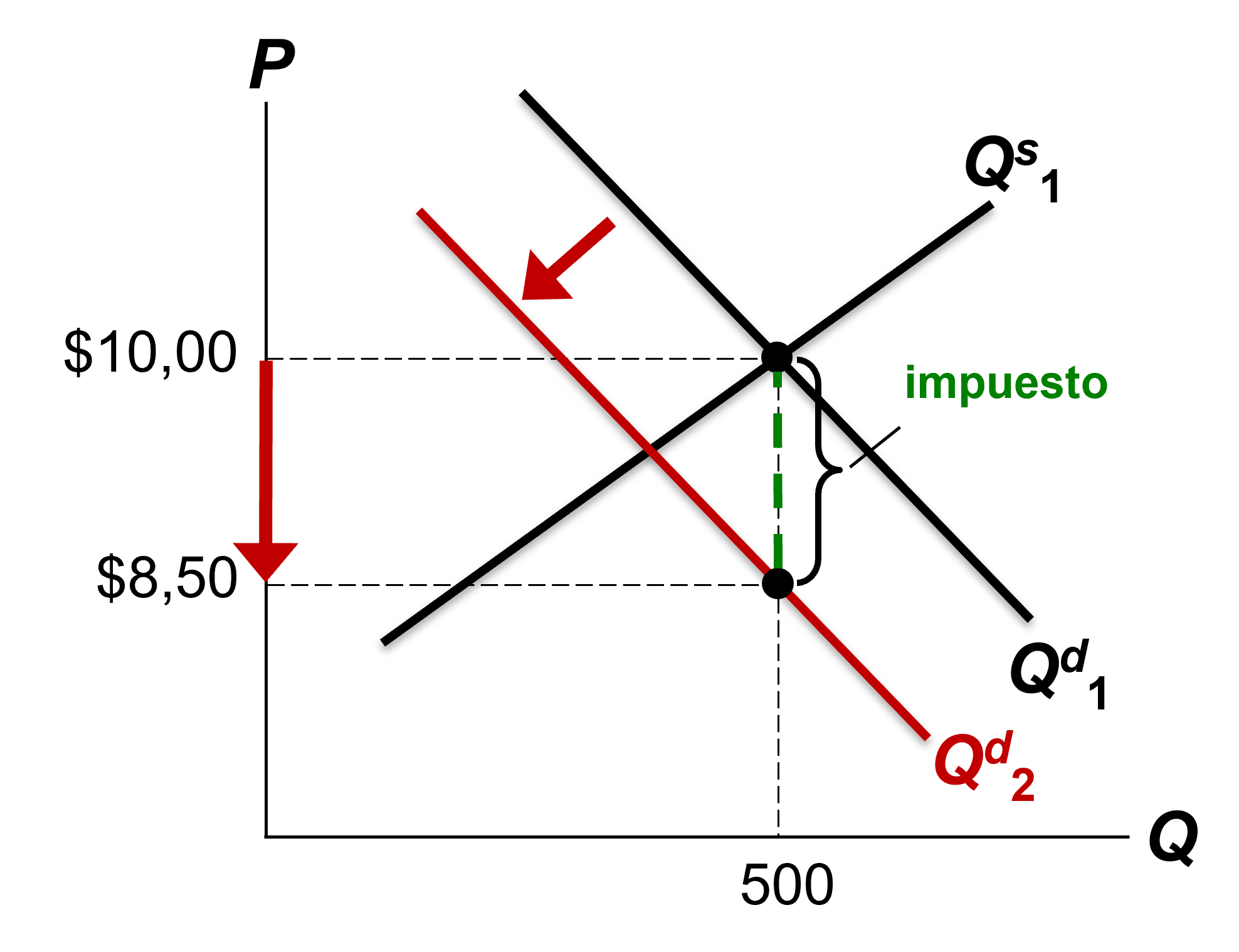
Un impuesto a los compradores desplaza la curva de demanda hacia abajo (izquierda) en el monto del impuesto.
P tendría que caer $1,50 para que los compradores estuvieran dispuestos a comprar el mismo Q que antes. Por ejemplo, si P cae de $10,00 a $8,50, los compradores aún están dispuestos a comprar 500 unidades.
Políticas del Gobierno y Mercado
Impuestos
Ejemplo. Parte 1: El gobierno impone un impuesto a los consumidores (cont.)
(ii) Nuevo equilibrio
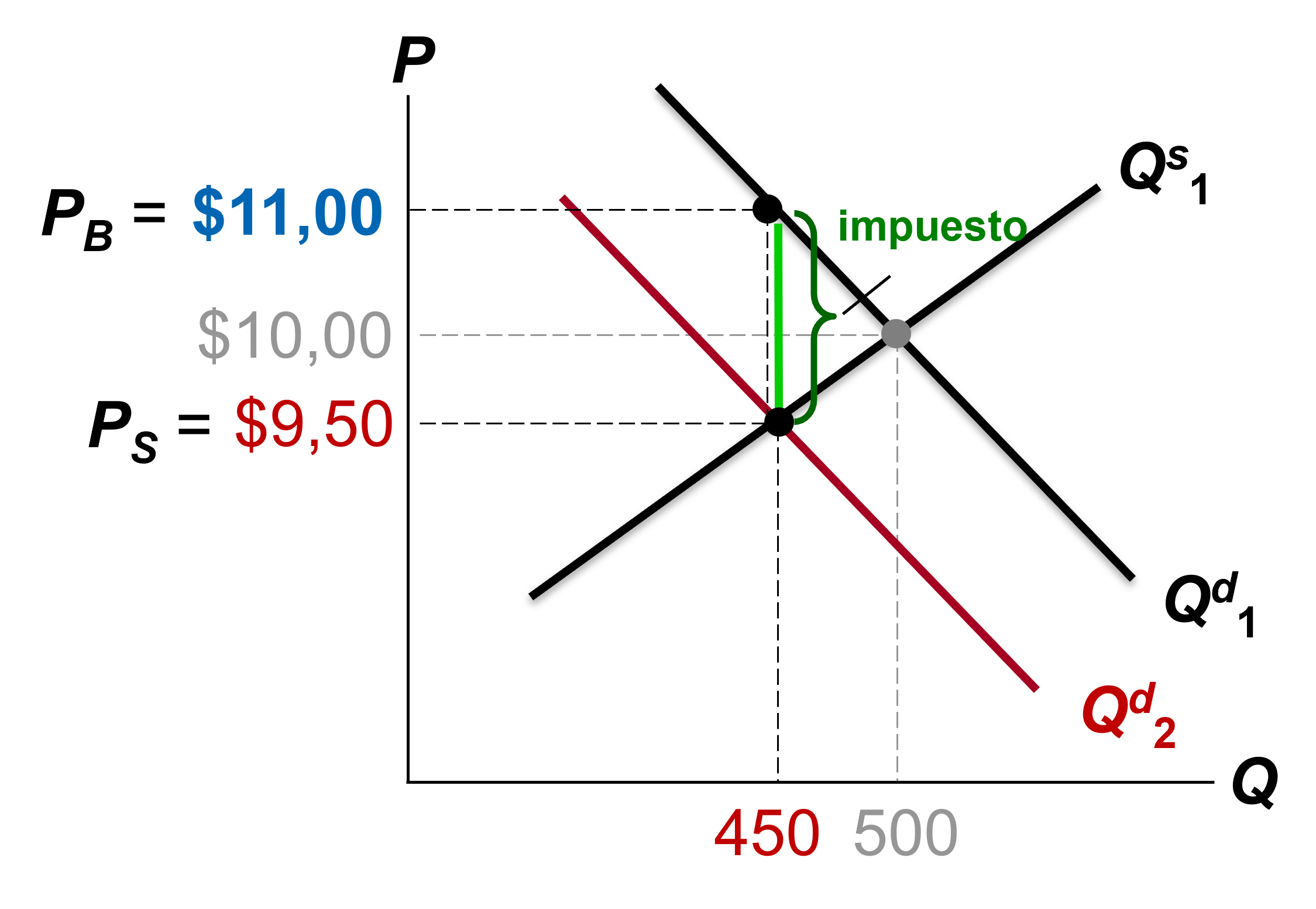
El nuevo equilibrio se da en Q = 450, para el cual los vendedores reciben \(P_s = \$9,5\) y los compradores pagan \(P_B = \$11,0\)
La diferencia entre ellos es igual a $1,50 (que es monto del impuesto).
Los compradores pagan $1,0 adicional y los vendedores reciben $0,5 menos.
Políticas del Gobierno y Mercado
Impuestos
Ejemplo. Parte 2: El gobierno impone un impuesto a los compradores
(i) Desplazamiento de la curva de oferta
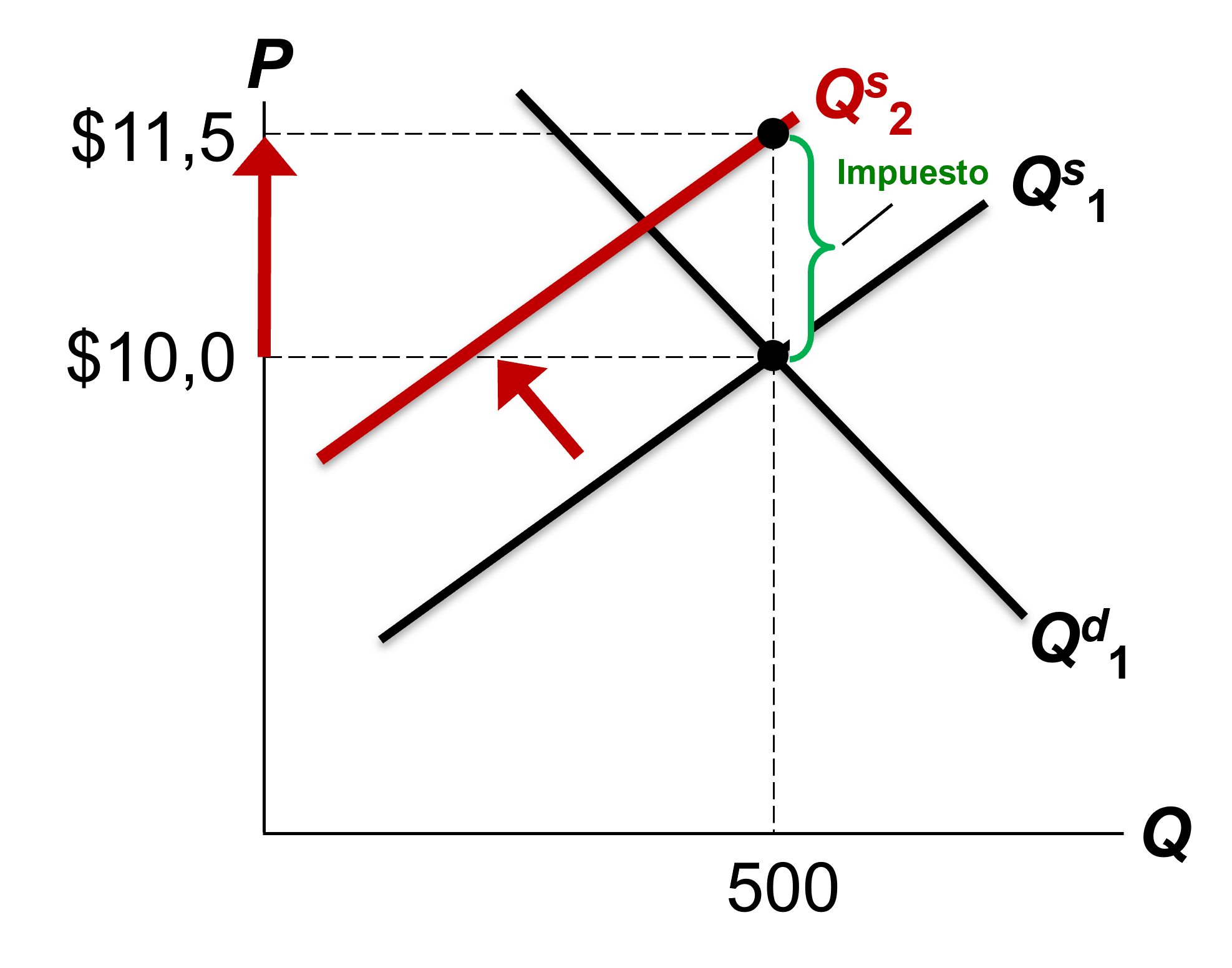
- El impuesto aumenta los costos de los vendedores en $1,50 por unidad.
- Los vendedores proporcionarán 500 unidades solo si P aumenta a $ 11,5, para compensar el aumento de costo.
- Por tanto, un impuesto a los vendedores desplaza la curva S hacia arriba en la cantidad del impuesto.
Políticas del Gobierno y Mercado
Impuestos
Ejemplo. Parte 2: El gobierno impone un impuesto a los productores (cont.)
(ii) Nuevo equilibrio
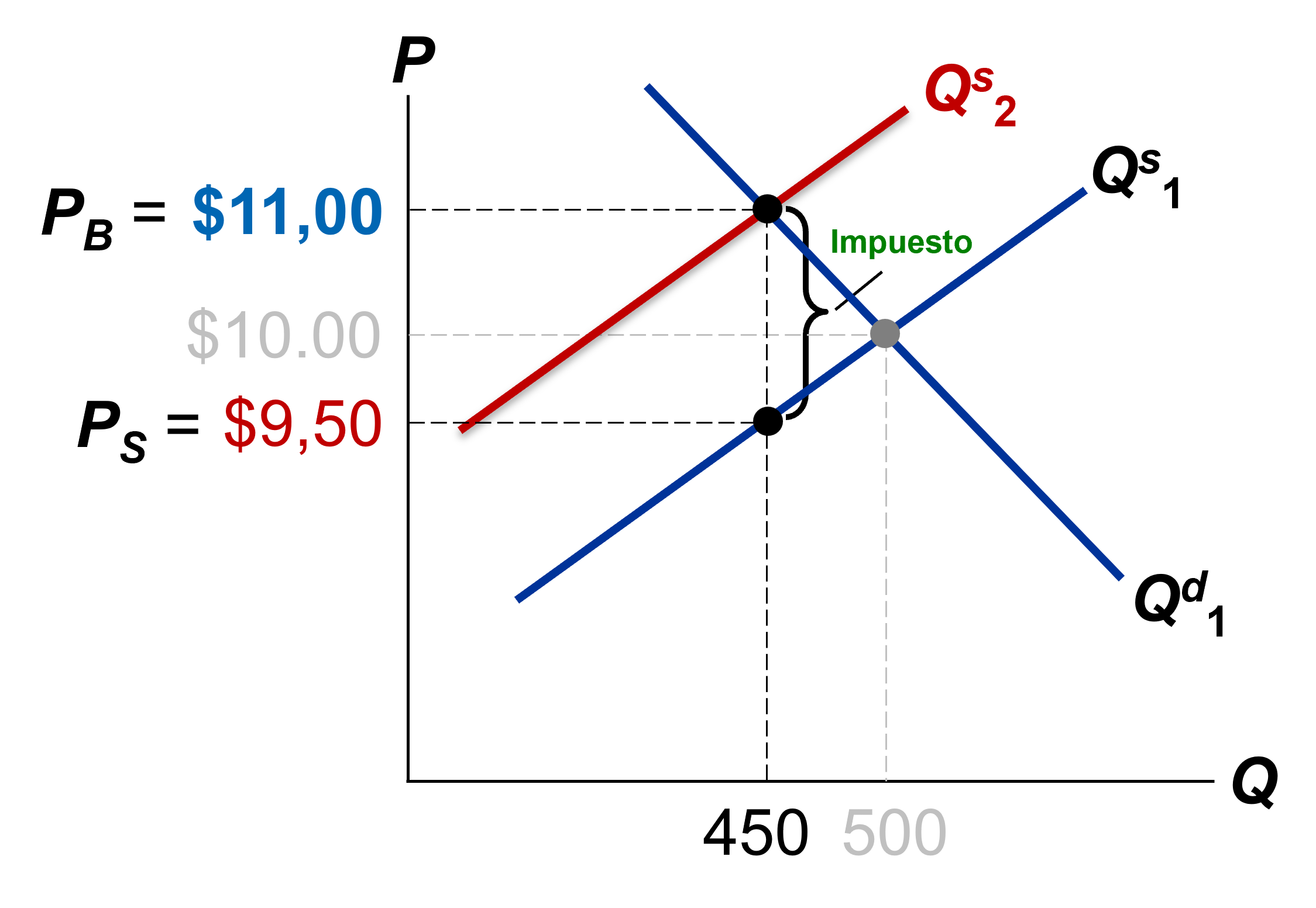
El nuevo equilibrio se da en Q = 450, para el cual los vendedores reciben \(P_s = \$9,5\) y los compradores pagan \(P_B = \$11,0\)
La diferencia entre ellos = $1,50 = impuesto
Los compradores pagan $1,0 adicional y los vendedores reciben $0,5 menos.
(Es decir, el mismo resultado de imponer sobre consumidores)
Políticas del Gobierno y Mercado
Impuestos
Ejemplo 2. Considerando la información en la tabla
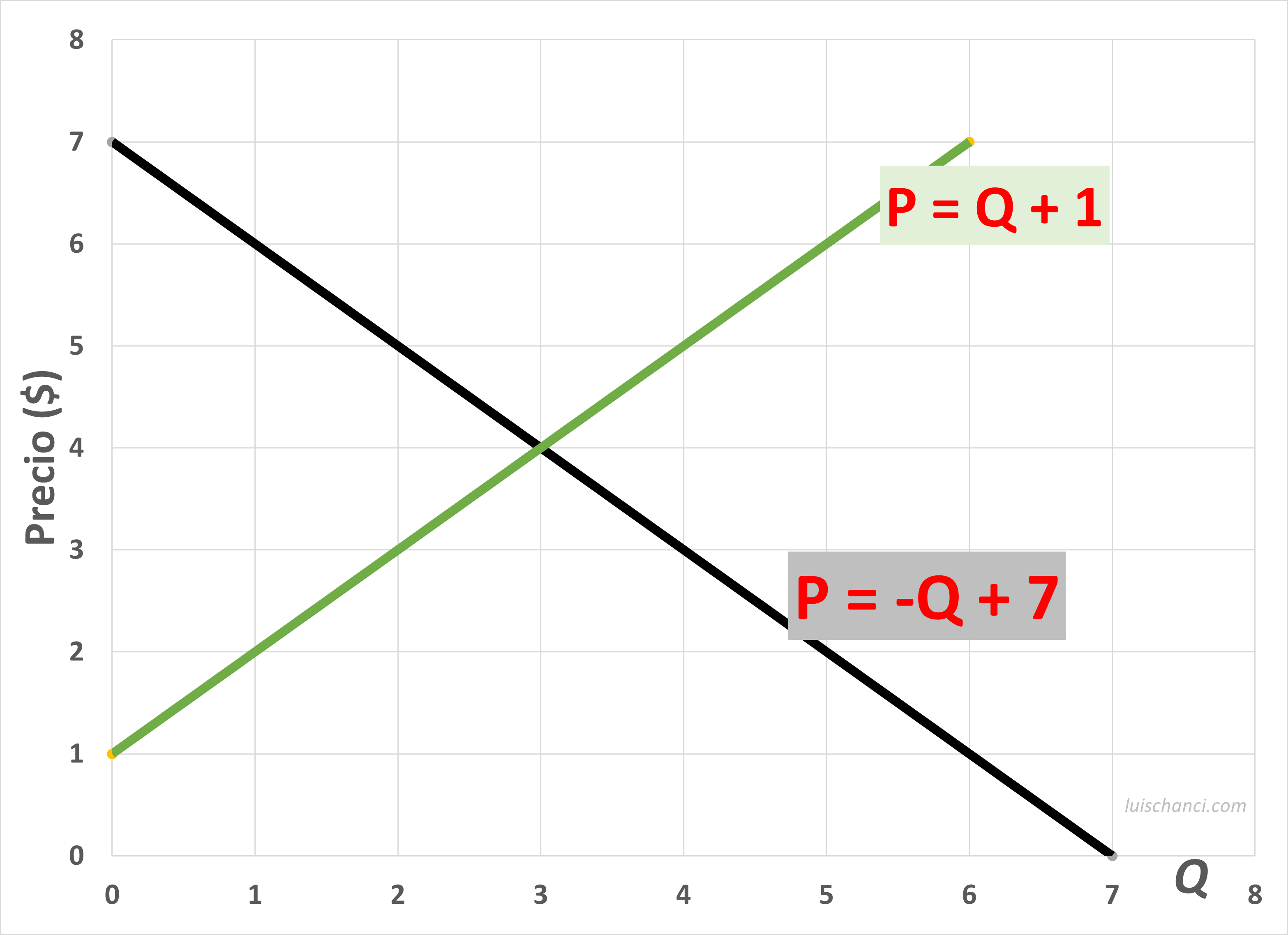
\[\begin{array}{|c|c|c|} \hline \textbf{Precio} & \textbf{Demanda} &\textbf{Oferta} \\ \hline \$0 & 7 & -\\ \$1 & 6 & 0\\ \$7 & 0 & 6\\ \hline \end{array}\]- Plantear las funciones inversas de demanda y oferta para este mercado. Luego encontrar el equilibrio y construir un gráfico.
- A medida que el precio sube de $2 a $3, ¿cuál es la elasticidad precio de la demanda? (utilizar el método del punto medio en los cálculos).
- Si se impone un precio de $5, en comparación con el equilibrio, ¿se produce un excedente o escasez (o ninguno)? ¿Cuál es el tamaño de este excedente o escasez?
- Supongamos que el gobierno impone un impuesto de T a los compradores. Mostrar la nueva ecuación de demanda. ¿Cuál es el nuevo precio para los compradores y vendedores? Representar gráficamente.
Políticas del Gobierno y Mercado
Ejemplo 2 (respuesta)
Funciones inversas de demanda y oferta y equilibrio:
\[\begin{eqnarray*} (P-0)&=&\frac{(7-0)}{0-7}(Q^d-7)\hspace{0.2cm}\Rightarrow\hspace{0.2cm}P=7-Q^d\\ (P-1)&=&\frac{(1-7)}{0-6}(Q^s-0)\hspace{0.2cm}\Rightarrow\hspace{0.2cm}P=1+Q^s \end{eqnarray*}\]
Por ende, el equilibrio es: \(P=3\) y \(Q=4\) .
Elasticidad: \[\left. \begin{array}{ccc} Si\,\,P=2&\Rightarrow&Q^d=7-2=5\\ Si\,\,P=3&\Rightarrow&Q^d=7-3=4 \end{array} \right\} \Rightarrow\,\, Elasticidad=\frac{\frac{(4-5)}{(4+5)/2}}{\frac{(3-2)}{(3+2)/2}}=-\frac{5}{9} \]
Si se impone un precio de $5: \[ \begin{array}{cccr} Q^d&=&7-P=7-5&=2\\ Q^s&=&-1+P=-1+5&=4\\ \hline Excedente&=&4-2&=2 \end{array} \]
Políticas del Gobierno y Mercado
Ejemplo 2 (respuesta)
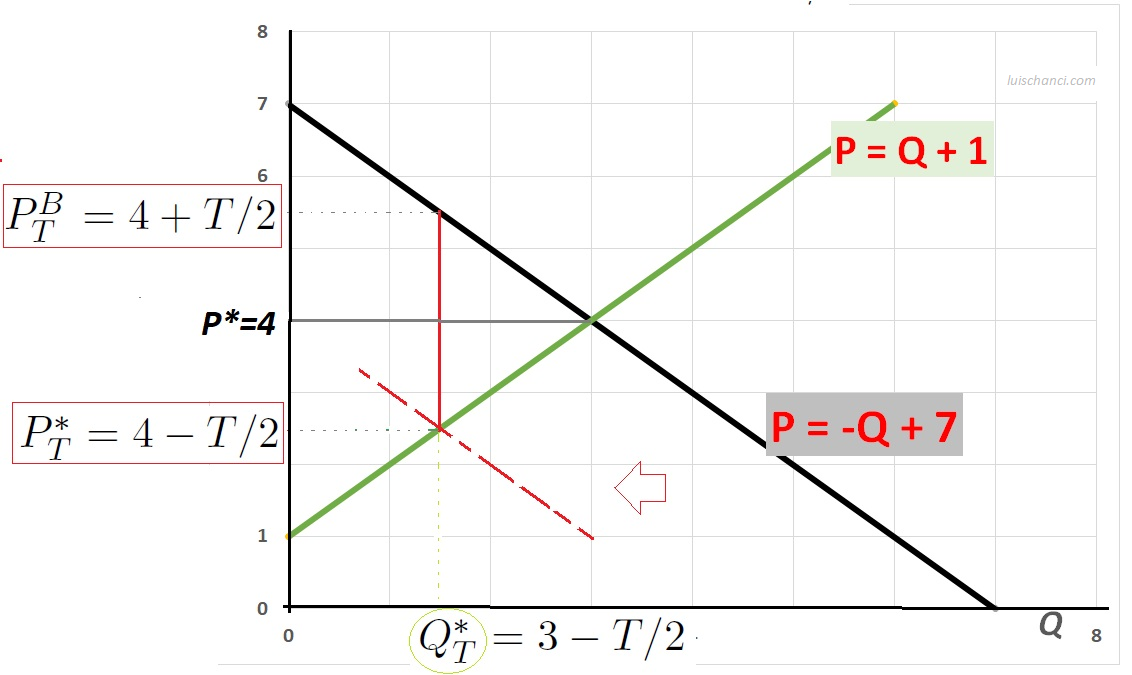
La función de demanda con el impuesto es \(Q^d_T=7-(P+T)\). Por ende, \[\left.\begin{array}{ccc} Q^d_T&=&7-(P+T)\\ Q^S_T&=&-1+P \end{array}\right\}\Rightarrow\,\, 7-(P^*_T+T)=-1+P^*_T\,\,\Rightarrow\,\, \left\{\begin{array}{c} P^*_T=4-T/2\\ Q^*_T=3-T/2 \end{array}\right. \]
Así, el precio que los compradores pagan es \(P^B_T=7-Q^*_T=7-(3-T/2)=4+T/2\) y los vendedores reciben \(P^s_T=P^*_T\).
Cierre
¿Preguntas?