Teoría del Consumidor

(Fundamentos) Microeconomía

Prof. Luis Chancí

Teoría del Consumidor

Teoría de la Conducta de los Consumidores: Descripción de cómo asignan los consumidores su renta entre los diferentes bienes y servicios para maximizar su bienestar.

La conducta de los consumidores se comprende mejor siguiendo tres pasos:
1. Las preferencias de los consumidores
2. Las restricciones presupuestarias
3. Las elecciones de los consumidores

Contenidos

Las Preferencias de los Consumidores
Las Restricciones Presupuestarias
Las Elecciones de los Consumidores
Otros temas:
- Preferencias Reveladas
- Índices de Costos de Vida

1. Las Preferencias

Las Preferencias

Cesta de mercado: Lista que especifica las cantidades de uno o más bienes.

Supongamos que le preguntamos a un consumidor si prefiere una cesta (o carro) de mercado, con cierta combinación de bienes, sobre otra.

Tabla: Ejemplo de Distintas Cestas de Mercado

Cesta	Alimentos	Vestido
A	20	30
B	10	50
D	40	20
E	30	40
G	10	20
H	10	40

Las Preferencias

Supuestos Básicos sobre las Preferencias

Completitud: Los consumidores pueden comparar y ordenar todas las cestas posibles. Es decir, dadas dos cestas de mercado A y B, un consumidor preferirá A a B, B a A, o se mostrará indiferente entre las dos.
Transitividad: Si un consumidor prefiere la cesta A a la B y la B a la C, entonces también prefiere la A a la C.
Cuánto más mejor: Los bienes son deseables, es decir, los consumidores siempre prefieren una cantidad mayor de cualquier bien a una menor.
Nota: se postula por que simplifica el análisis. Pero, algunos bienes, como la contaminación, pueden no ser deseables.

Las Preferencias

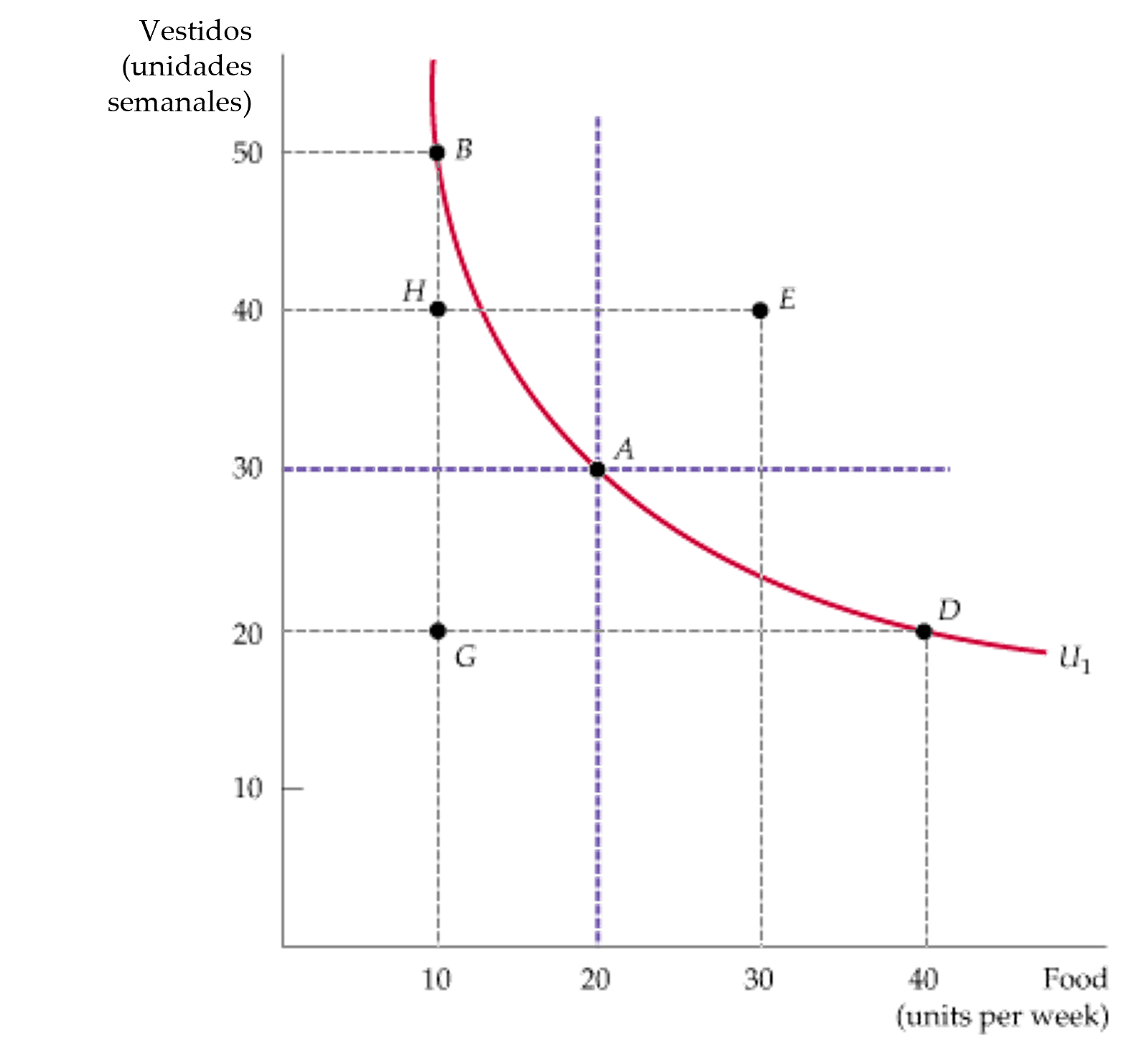
Curva de Indiferencia Representa todas las combinaciones de cestas de mercado que reportan el mismo nivel de satisfacción a un consumidor.

Figura: Curva de Indiferencia

La curva de indiferencia U1 que pasa por la cesta de mercado A muestra todas las cestas que reportan al consumidor el mismo nivel de satisfacción que la A; esto comprende las cestas de mercado B y D.

Las Preferencias

Mapa de Curva de Indiferencia gráfico que contiene un conjunto de curvas de inderencia que muestran las cestas de mercado en que es indeferente un consumidor.

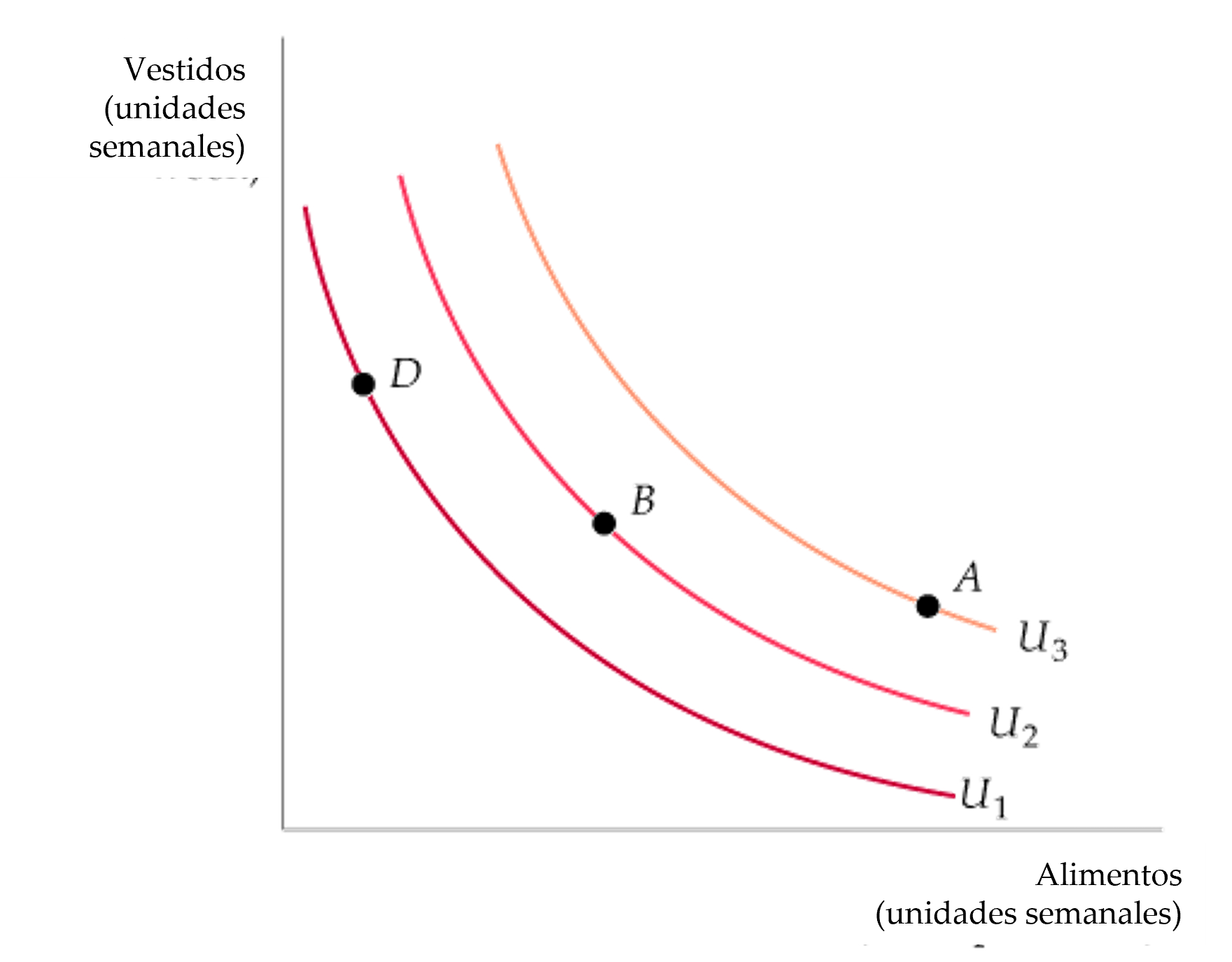
Figura: Mapa de Curva de Indiferencia

Un mapa de curva de indiferencia es un conjunto de curvas de indiferencia que describen las preferencias de una persona.
Se prefiere cualquier cesta de mercado situada en la curva de indiferencia U3, como la A, es preferida a cualquier cesta de mercado situada en la curva U2 (ej., cesta B), la cual se prefiere, a su vez, a cualquiera situada en U1, como la D.

Las Preferencias

Las Curvas de Indiferencia no Pueden Cortarse

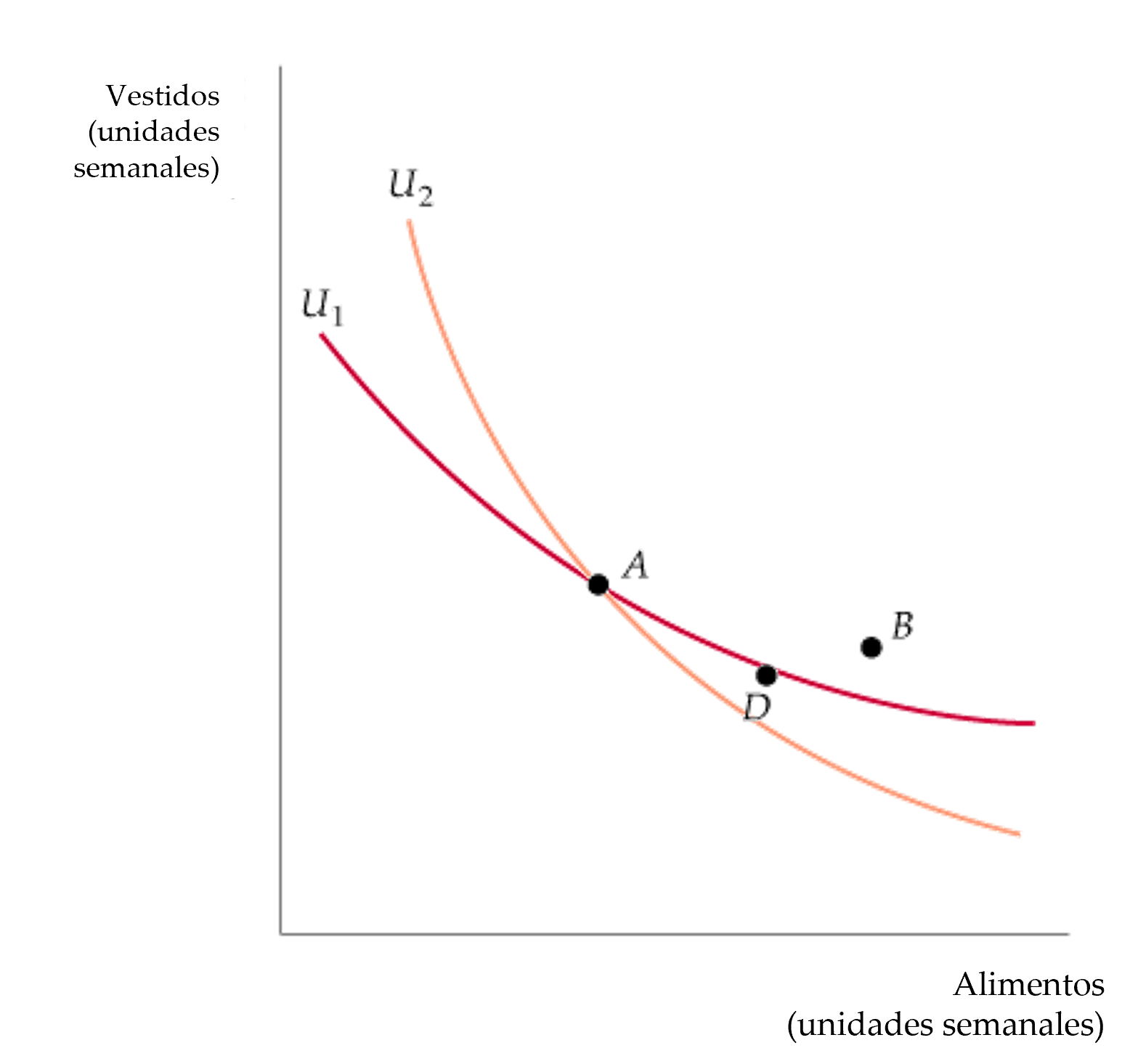
Figura: Curvas de Indiferencia

Si las curvas de indiferencia U1 y U2 se cortaran, se violaría uno de los supuestos de la teoría del consumidor.

Las Preferencias

Relación Marginal de Sustitución (RMS) Cantidad máxima de un bien a la que está dispuesta a renunciar una persona para obtener una unidad más de otro.

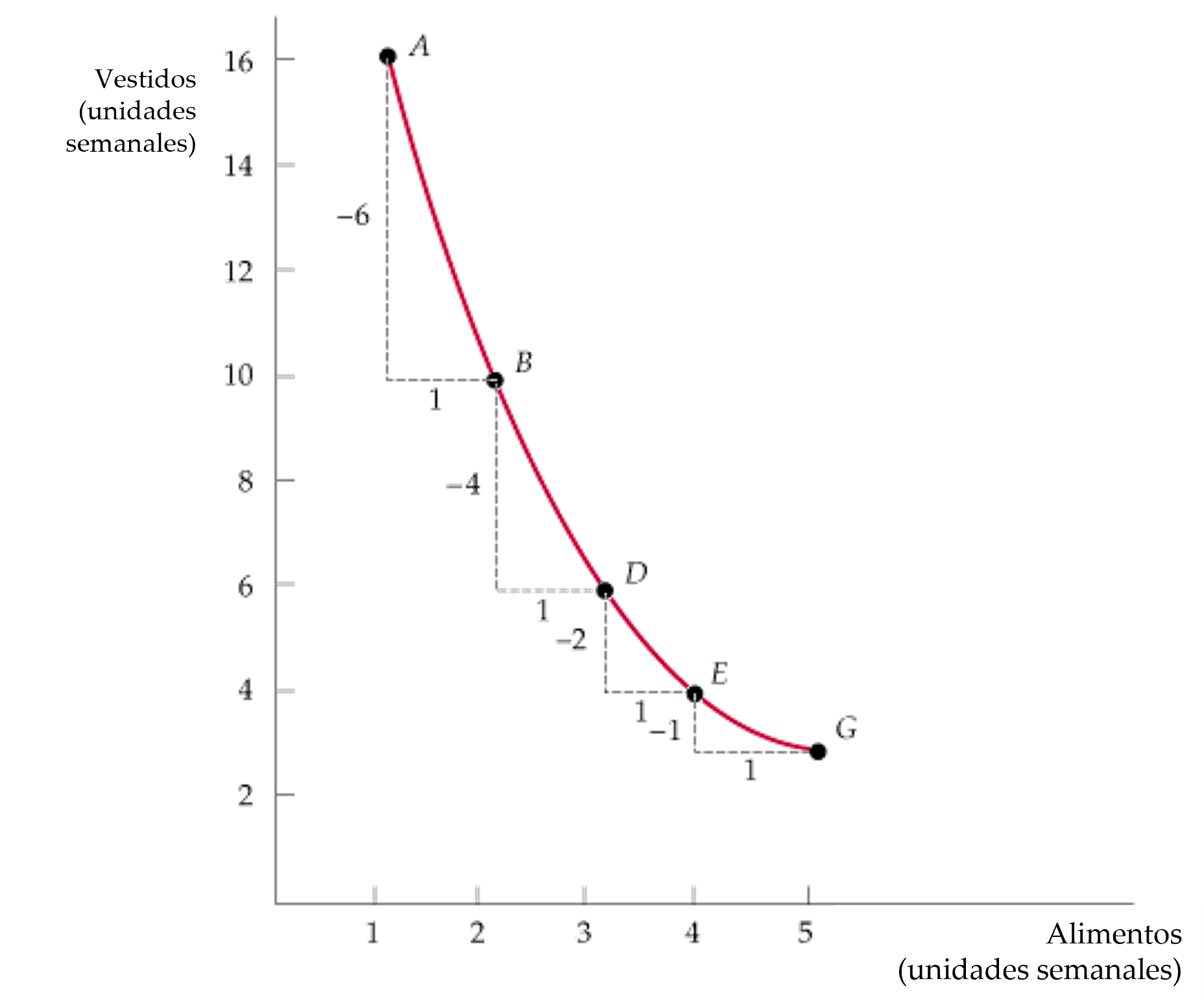
Figura: Relación Marginal de Sustitución

La pendiente de una curva de indiferencia mide la relación marginal de sustitución (RMS) del consumidor entre dos bienes.
Convexidad Cuando la RMS disminuye a lo largo de una curva de indiferencia, esta es convexa.
En el ejemplo de la figura, al pasar de A a B: \[RMS_{A,B}=\frac{\Delta V}{\Delta A}=-6\]

Las Preferencias

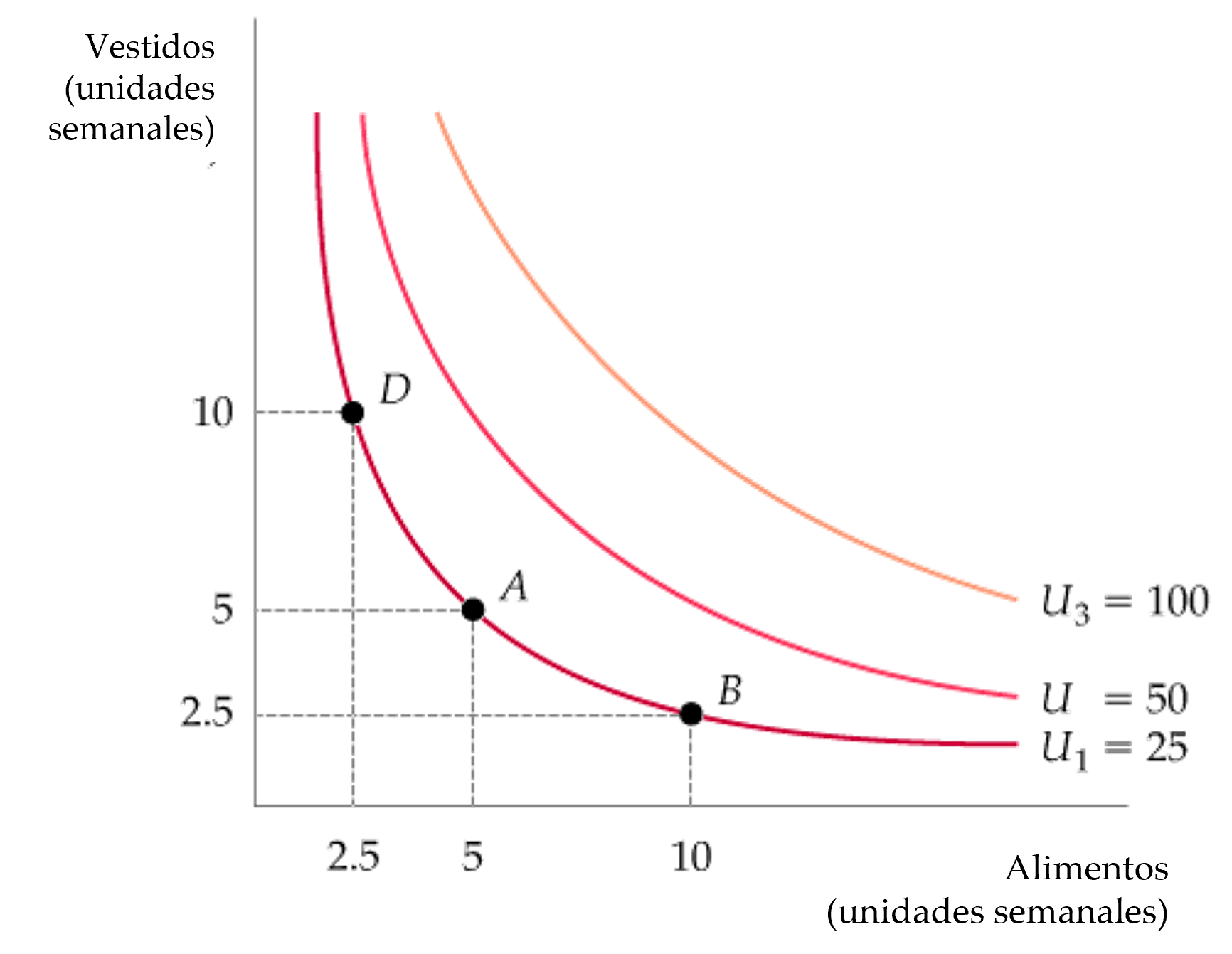
Función de Utilidad La función de utilidad puede representarse con un conjunto de curvas de indiferencia, cada una de las cuales lleva un indicador numérico.

Figura: Funciones de Utilidad

La función de utilidad puede representarse con un conjunto de curvas de indiferencia, cada una de las cuales lleva un indicador numérico. Por ejemplo, \[U(V,A)=V^{1/2}A^{1/2}\]
Esta figura muestra tres curvas de indiferencia (cuyos niveles de utilidad son 25, 50, y 100, respectivamente) relacionados con la función de utilidad AC: \[U(V,A)=V\cdot A\]

Las Preferencias

Relación entree Utilidad Marginal y la Relación Marginal de Sustitución

Utilidad marginal (UM) Satisfacción adicional que se obtiene consumiendo una unidad más de un bien. Por ejemplo, abusando de la notación matemática, para $U(V,A)=V^{1/2}A^{1/2}$ se tendría algo como \[UM_V=\frac{\Delta U(V,A)}{\Delta V}\equiv(1/2)V^{-1/2}A^{1/2}\] Utilidad marginal decreciente: Principio según el cual cuanto más se consume de un bien, menos aumenta la utilidad con el consumo de más cantidades.
Relación entre la RMS (pendiente de la curva de indiferencia) y la pendiente de la curva de utilidad (relación entre utilidades marginales): \[RMS=\frac{\Delta V}{\Delta A}=-\frac{\Delta U(V,A)/\Delta A}{\Delta U(V,A)/\Delta V}=-\frac{UM_A}{UM_A}\]

Las Preferencias

Otras formas/curvas

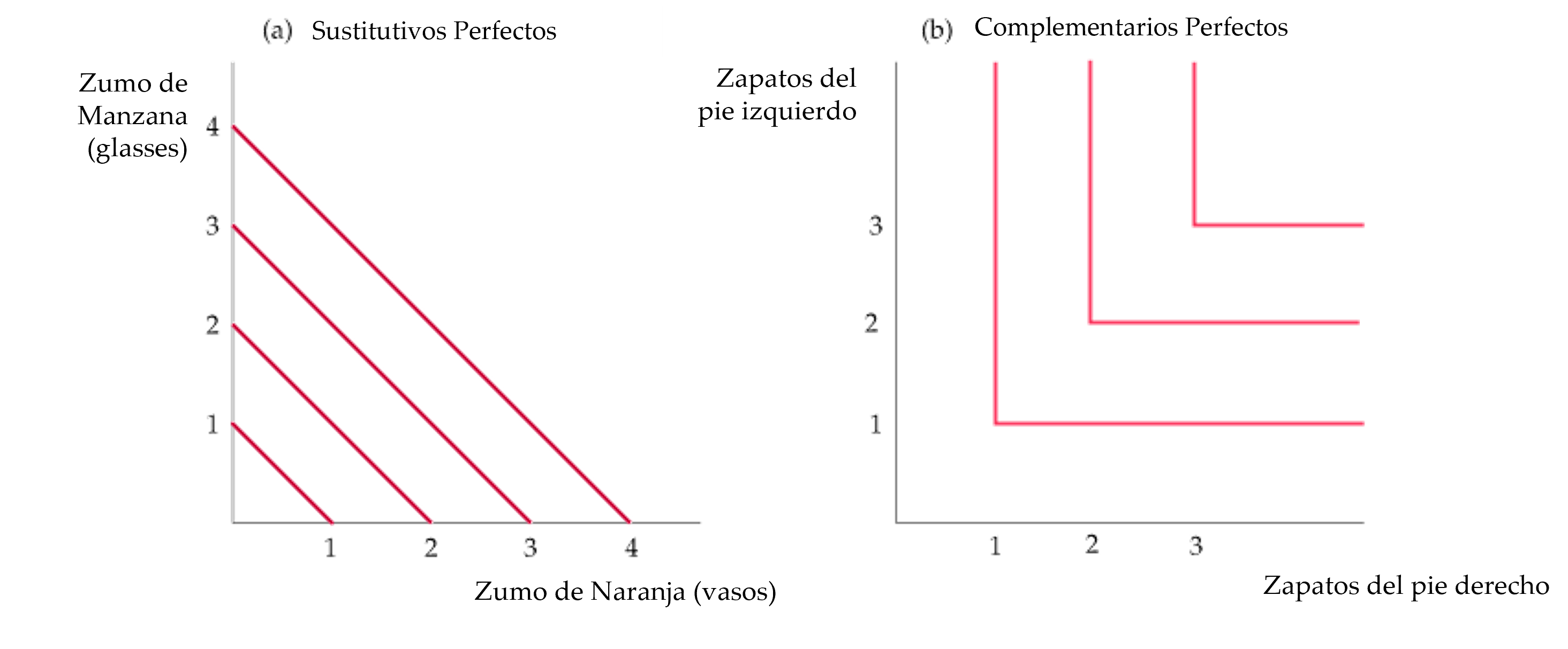
Sustitutivos Perfectos: Dos bienes cuya relación marginal de sustitución es una constante.
Complementarios Perfectos: Dos bienes cuya RMS es infinita; las curvas tienen forma de ángulo recto.
Mal: Un bien es un mal cuando se prefiere una cantidad menor a una mayor.

2. La Restricción de Presupuesto

La Restricción de Presupuesto

Restricciones presupuestarias: Restricciones a las que se enfrentan los consumidores como consecuencia de su renta limitada.
Recta presupuestaria: Todas las combinaciones de bienes con las que la cantidad total de dinero gastada es igual a la renta.

Por ejemplo, para los bienes Vestido (V) y Alimento (A), el gasto en cierta cantidad de bienes (A,V), cuyos precios son $P_A=\$1$ y $P_V=\$2$, es cubierto con un ingreso de $80: \[P_V V + P_AA =I \hspace{2cm}\rightarrow\hspace{2cm} A+2V=\$80\]

La Restricción de Presupuesto

La recta de presupuesto y su pendiente

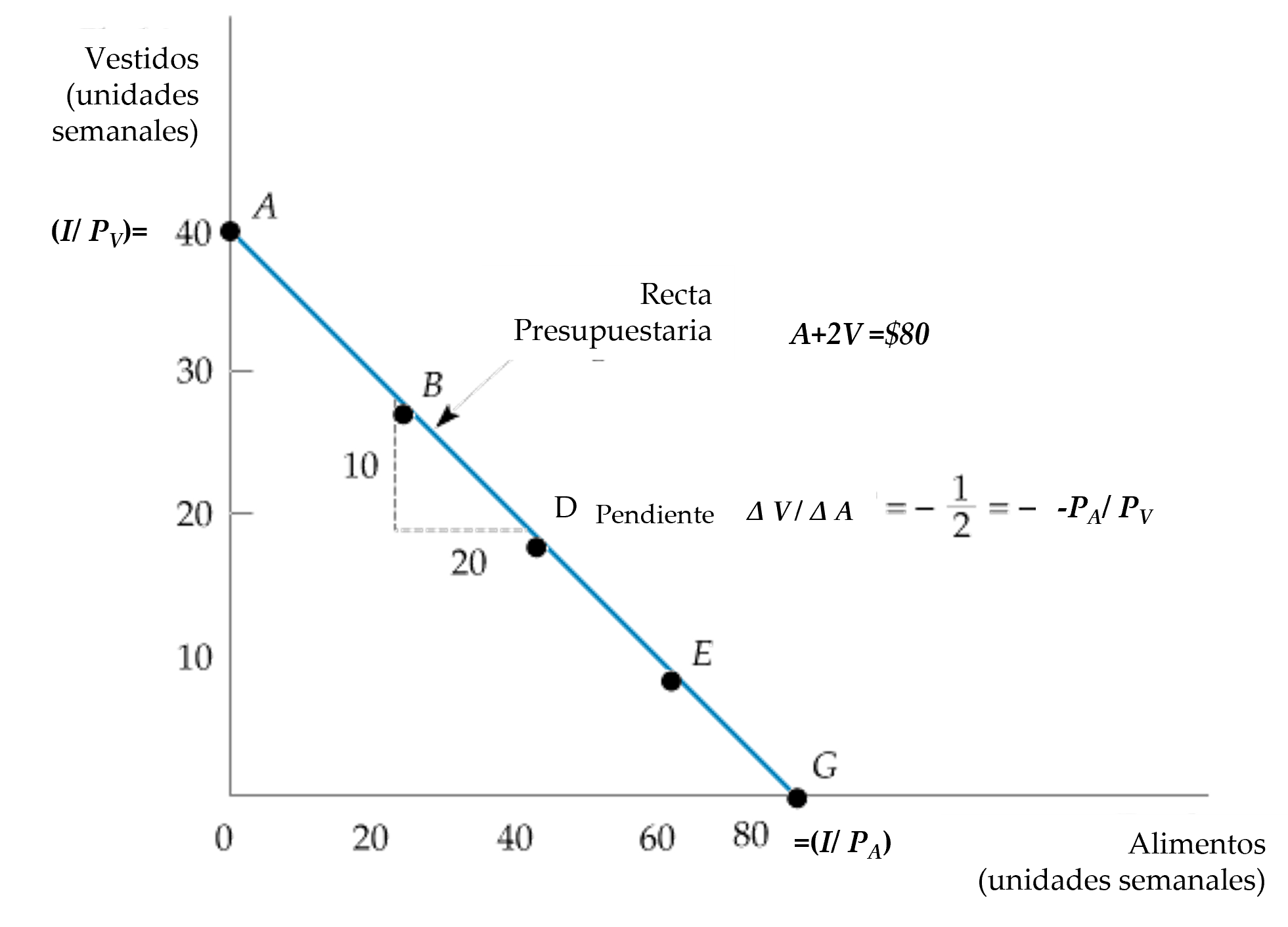
Figura: Cesta de Mercado y la Recta Presupuestaria

Una recta presupuestaria describe las combinaciones de bienes que pueden comprarse dada la renta del consumidor y los precios de los bienes.
La recta $AG$ (que pasa por los puntos B, D y E ) muestra el presupuesto correspondiente a una renta de $80. Un precio de los alimentos de $P_A = \$1$ por unidad y el precio del vestido $P_V = \$2$ por unidad.
La pendiente de la recta presupuestaria (medida entre los puntos B y D) es $-P_A/P_V = -10/20 = -1/2$ .

La Restricción de Presupuesto

Ejemplo:

Supongamos que cuando Luis visita el supermercado busca dos bienes: Mangos (M) y Arroz (A). El ingreso de Luis es $1200 y los precios de los bienes son $P_A = \$4/kg$ y $P_M = \$1/kg$.

Si Luis se gasta todo su ingreso en arroz. ¿Cuántos kilos podría comprar?
Si Luis se gasta todo su ingreso en mangos. ¿Cuántos kilos podría comprar?
Si Luis compra 100 kilos de arroz. ¿Cuántos kilos de mango puede comprar?
Construir un gráfico que represente la restricción presupuestaria.
Determinar la pendiente de la recta de presupuesto.

La Restricción de Presupuesto

Ejemplo (respuesta)

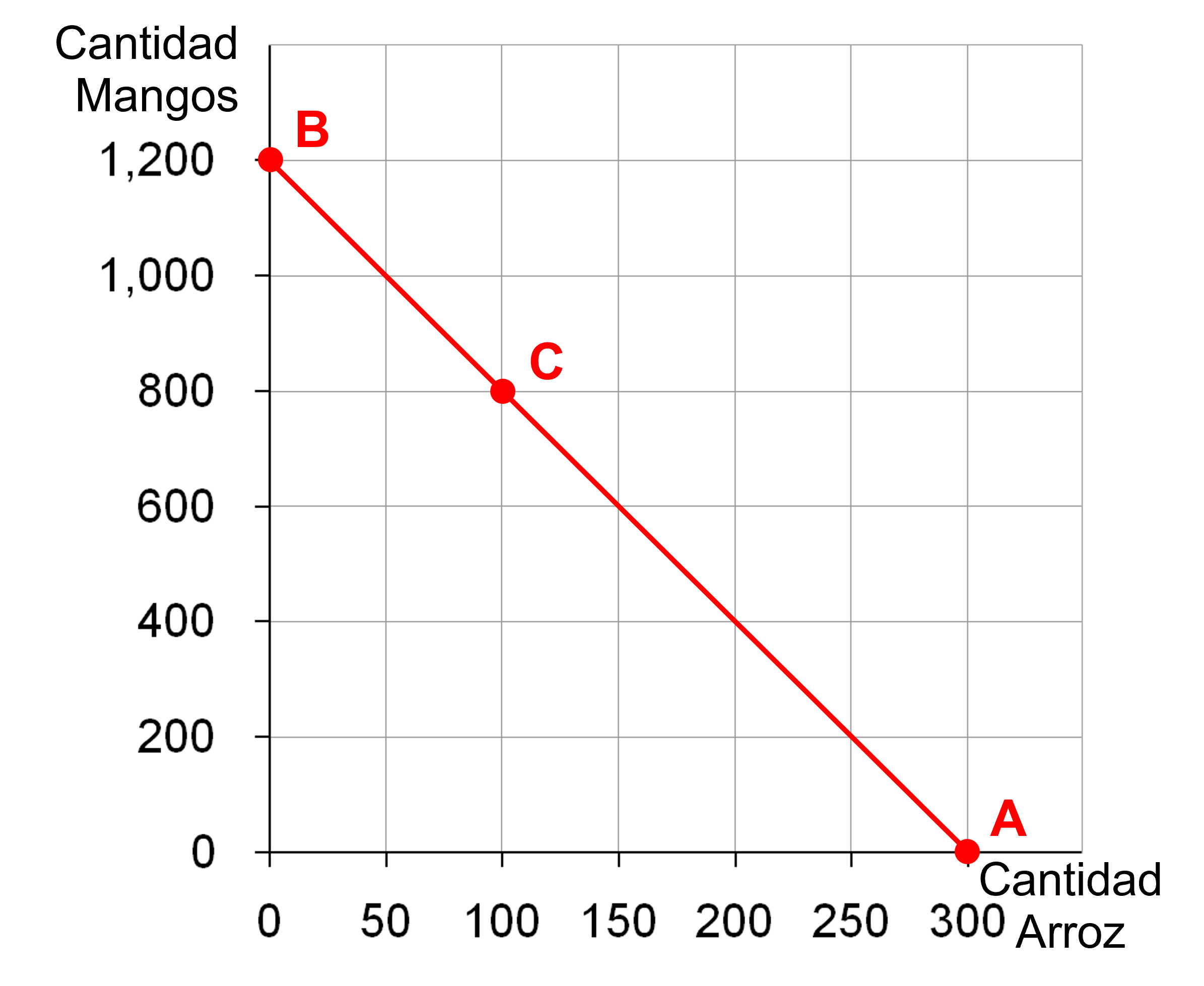
Si se gasta todo en A (punto A en la figura:
( 1200 / 4 = 300 ) kilos de arroz
Si se gasta todo en M (punto B en la figura):
( 1200 / 1 = 1200 ) kilos de mangos
Si Luis compra 100 kilos de arroz, que cuestan $400, le quedan $800 para comprar 800 mangos (punto C).
La pendiente es $-|P_A/P_M|=-(\$4/\$1)=-4$

Variación en el Ingreso (o Renta)

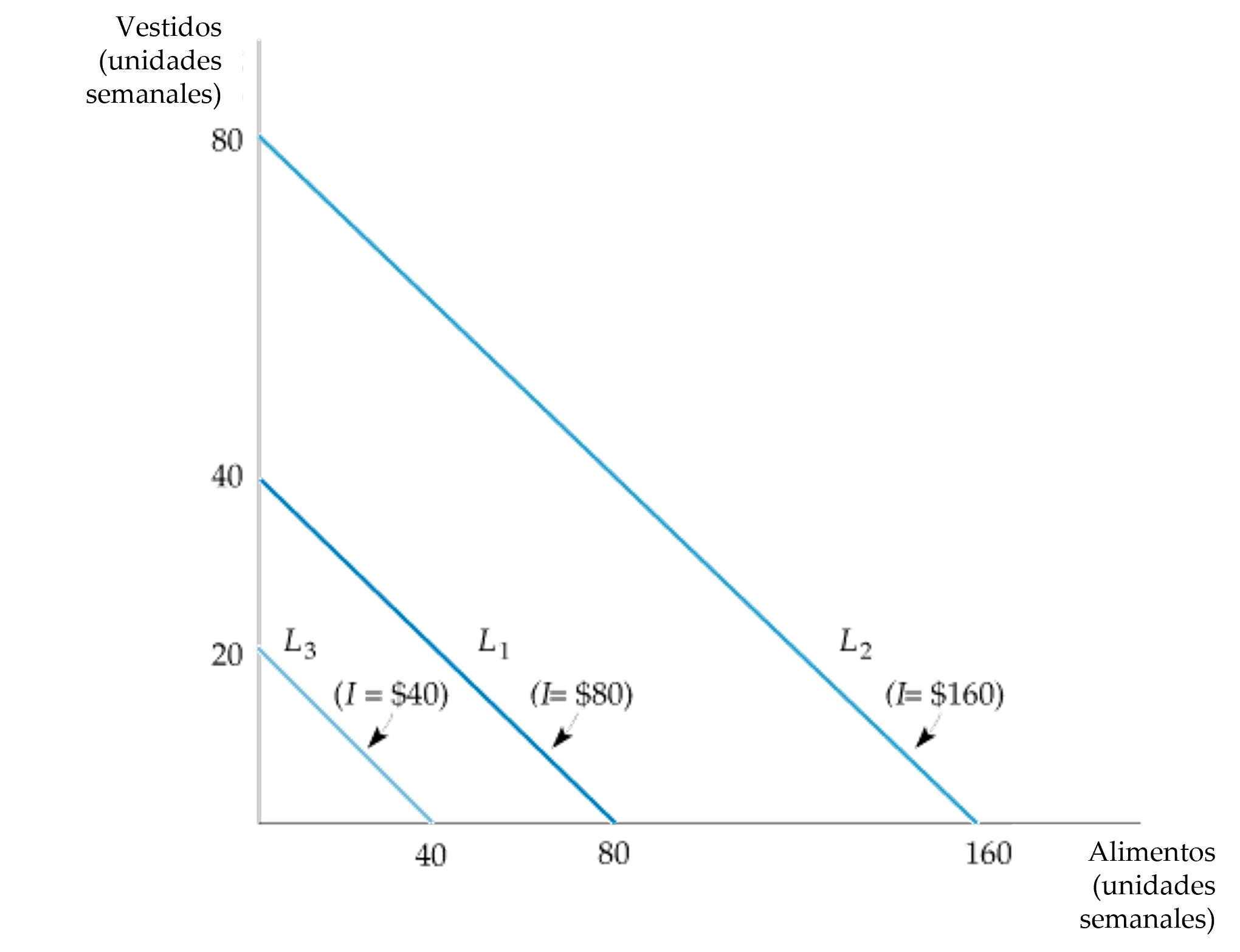
Figura: Efectos de una Variación de la Renta en la Recta Presupuestaria

Una variación en la renta (sin que varíen los precios) provoca un desplazamiento de la recta presupuestaria paralelo a la recta inicial (L1).
Cuando se incrementa la renta de $80 (situada en L1) a $160, la recta presupuestaria se desplaza hacia afuera a L2.
Si la renta desciende a $40, la recta se desplaza hacia dentro a L3.

La Restricción de Presupuesto

Ejemplo: Supongamos en el ejemplo de magos y arroz que ahora que el ingreso total baja a $800. ¿Cómo cambia el gráfico?

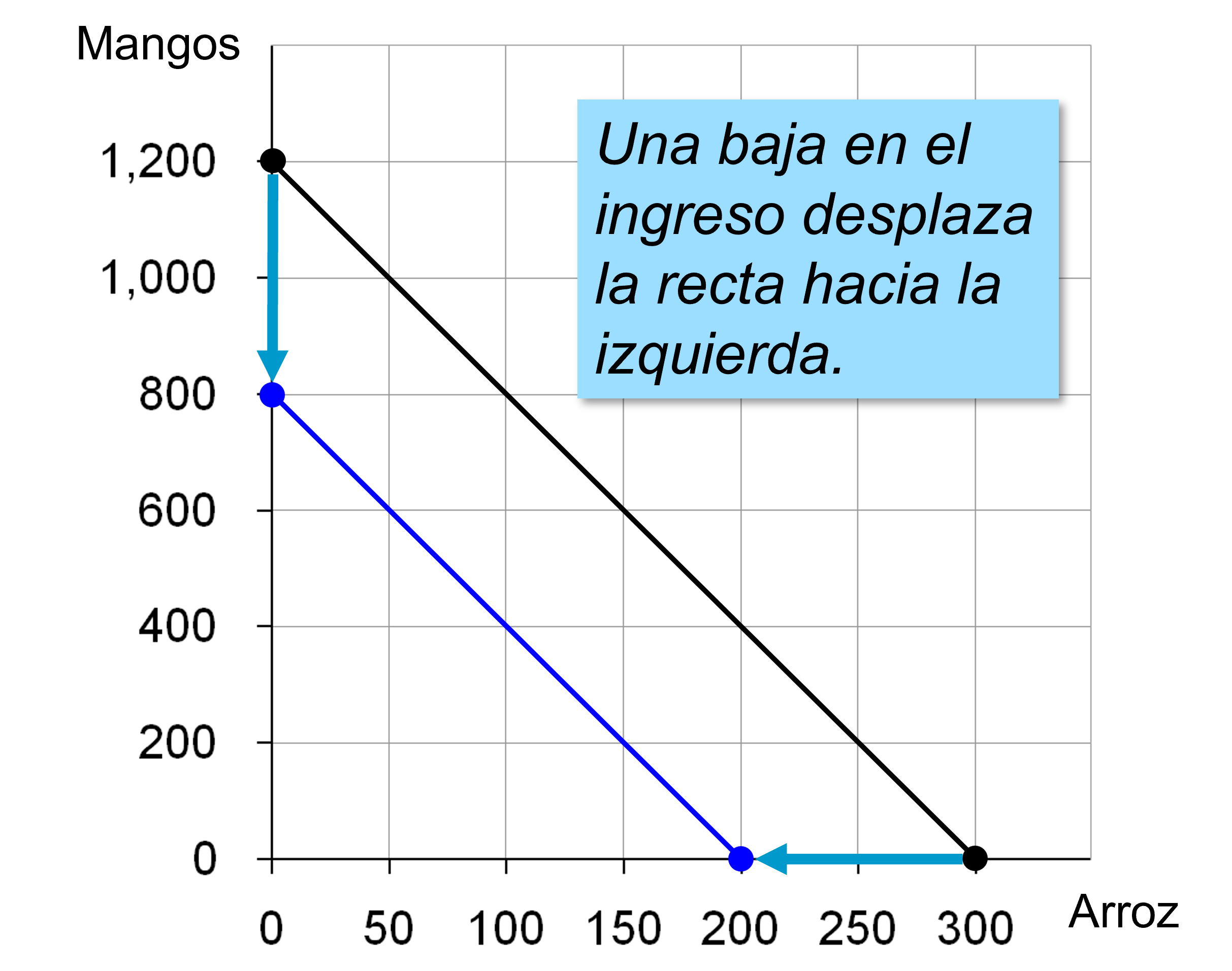
La Restricción de Presupuesto

Variaciones de los Precios

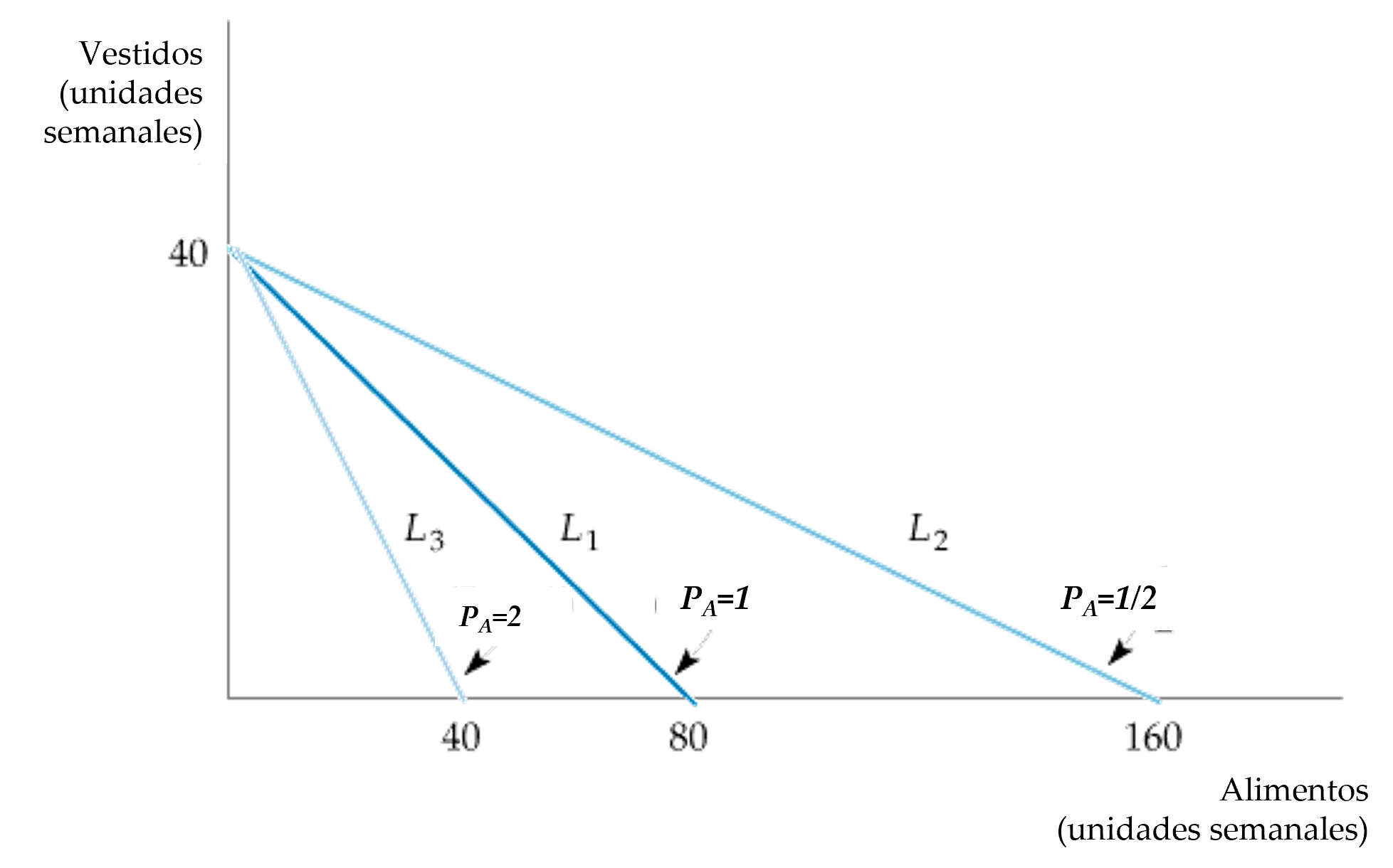
Figura: Efectos de una Variación de un Precio en la Recta Presupuestaria

Una variación del precio de uno de los bienes (sin que varíe la renta) provoca un giro de la recta presupuestaria en torno a una de las coordenadas en el origen.
Cuando baja el precio de los alimentos de $1.00 a $0.50, la recta presupuestaria gira hacia afuera de L1 a L2.
Sin embargo, cuando el precio sube de $1.00 a $2.00, la recta gira hacia adentro de L1 a L3.

La Restricción de Presupuesto

Ejemplo: Supongamos en el ejemplo de magos y arroz que ahora que el precio de los mangos sube a $2. ¿Cómo cambia el gráfico?

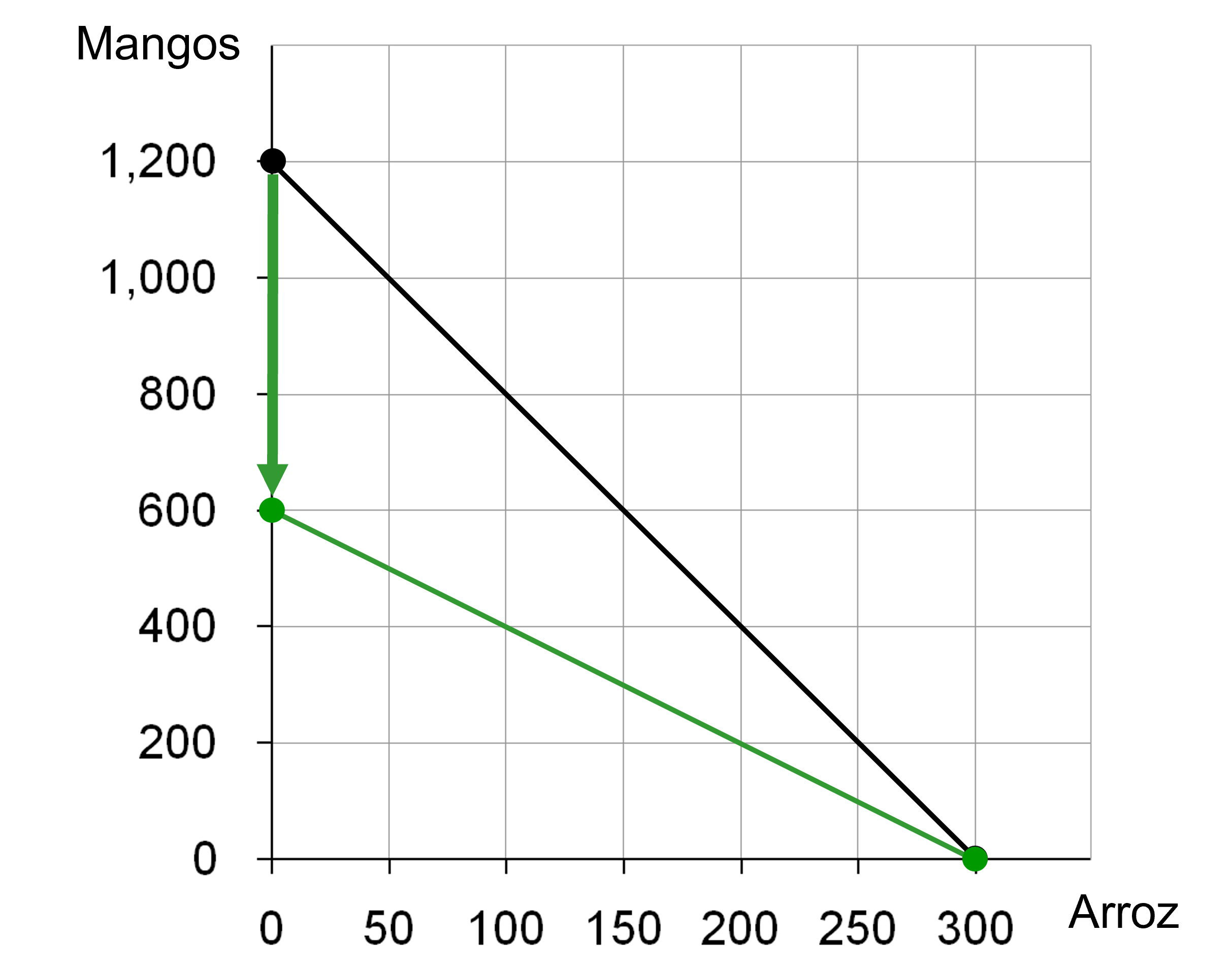
3. La Elección (El Óptimo)

La Elección (El Óptimo)

La cesta de mercado maximizadora tiene que satisfacer dos condiciones:

Debe encontrarse en la recta presupuestaria.
Debe suministrar al consumidor la combinación de bienes y servicios por la que muestra una preferencia mayor.

De forma intuitiva, los consumidores buscarán la combinación de bienes que les de la mayor utilidad posible, pero considerando la restricción que enfrentan en el presupuesto (maximizar U sujeto a R.P).

La Elección (El Óptimo)

Beneficio Marginal y Costo Marginal

El resultado óptimo es simplemente algo que vimos como el principio de los agentes marginalistas: los agentes toman una decisiones a partir de comparar el beneficio o utilidad marginal con el costo marginal.

Beneficio marginal: Es el beneficio generado por el consumo de una unidad más de un bien.
- El beneficio marginal se mide por los cambios relativos en las utilidades marginales. Es decir, la RMS.
Costo marginal: Es el costo de una unidad más de un bien.
- El costo marginal en este caso estará determinado por los precios relativo, que es el costo de una unidad más de alimentos. Es decir, la pendiente de la restricción de presupuesto.

La Elección (El Óptimo)

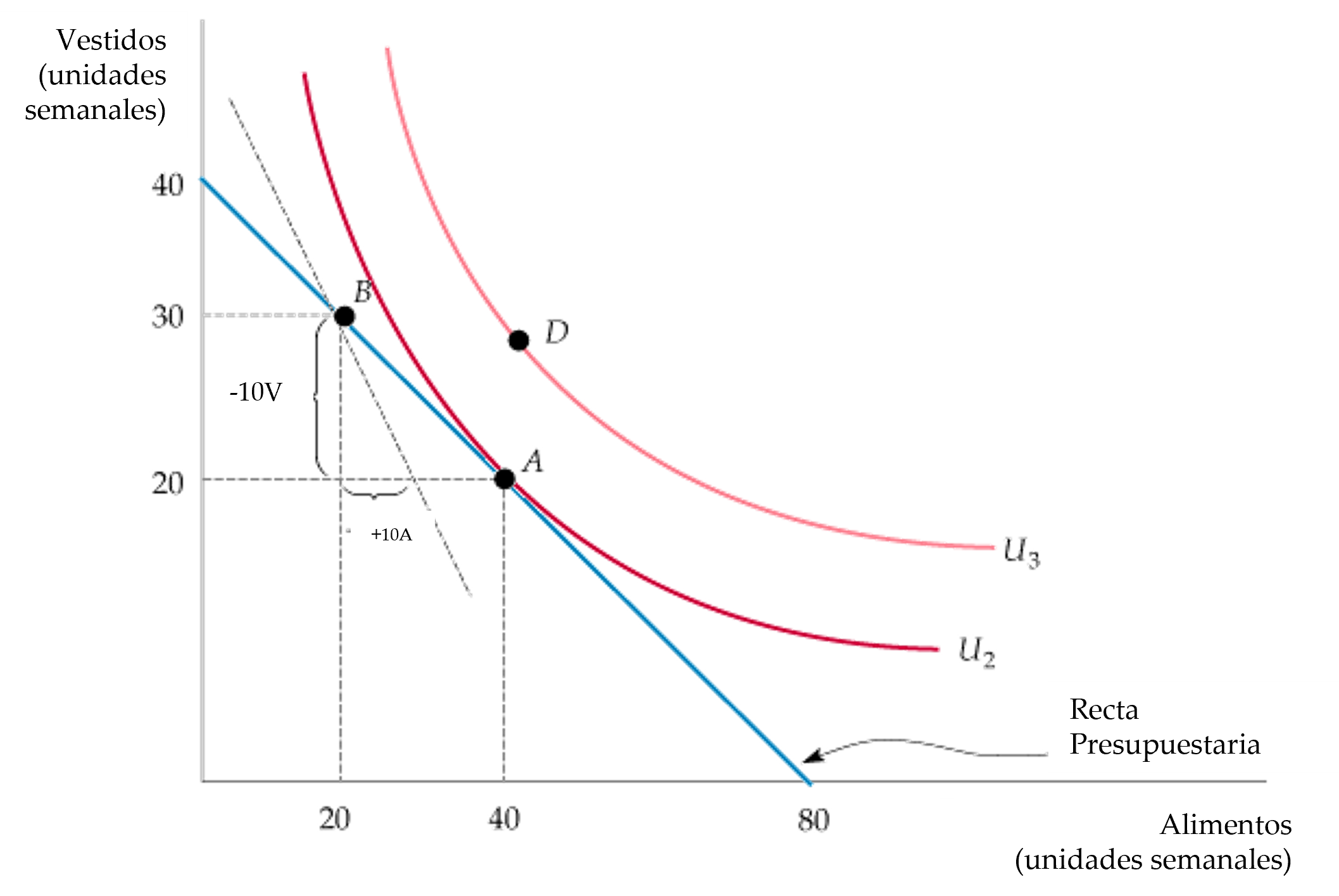
Figura: Beneficio Marginal y Costo Marginal

Alternativamente, desde la matemática, se puede ver el punto óptimo como un punto tangente en el cual las pendientes de la curva de indiferencia (que es la RMS) se hace igual a la pendiente de la restricción de presupuesto (que es la relación de precios).
No es posible alcanzar ningún nivel de satisfacción más alto (e.g., la cesta de mercado D).
En A, que es el punto de maximización, la RMS entre los dos bienes es igual a la relación de precios. En B, sin embargo, la RMS es ([-(-10/10) = 1]), mayor que la relación de precios ((1/2)), por lo que no se maximiza la satisfacción.

La Elección (El Óptimo)

Matemáticamente, igualando la pendiente de ambas curvas, el punto de elección (el óptimo o punto de tangencia) se puede escribir como \[|RMS_{V,A}|=|P_A/P_V|\]

Principio equimarginal: Principio según el cual la utilidad se maximiza cuando un consumidor ha igualado la utilidad marginal de cada peso gastado en cada bien:

\[RMS_{V,A} = \frac{UM_A}{UM_V}=\frac{P_A}{P_V}\] Es decir, \[\frac{UMA}{P_A} = \frac{UMV}{P_V}\]

La Elección (El Óptimo)

Ejemplo

Volvamos al ejemplo en donde $U(V,A)=V^{1/2}A^{1/2}$. Las funciones de utilidad marginal son:
\[UM_V=(1/2)V^{-1/2}A^{1/2}\hspace{2cm}y\hspace{2cm} UM_A=(1/2)V^{1/2}A^{-1/2}\]
Además, retomemos los datos del ejemplo de la restricción de presupuesto: $P_A=\$1$, $P_V=\$2$ y $I=\$80$. Es decir, la recta presupuestaria era \[A+2V=80\] y la pendiente estaba dada por $-P_A/P_V=-1/2$.
Encontrar los niveles de consumo de $A$ y $V$.

La Elección (El Óptimo)

Ejemplo (respuesta)

Primero planteamos la RMS y la condición de optimalidad (en valor absoluto): \[RMS=\frac{(1/2)V^{1/2}A^{-1/2}}{(1/2)V^{-1/2}A^{1/2}}=\frac{P_A}{P_V}=\frac{1}{2}\] Condición que se puede simplificar como $2V=A$.
La segunda ecuación es la recta de presupuesto: \[A+2V=80\]
Así, al resolver el sistema (dos ecuaciones con dos incognitas) se obtiene: \[V=20\hspace{1cm},\hspace{1cm}A=40\]

La Elección

Soluciones de Esquina Situación en que la relación marginal de sustitución de un bien de una cesta elegida no es igual a la pendiente de la recta presupuestaria.

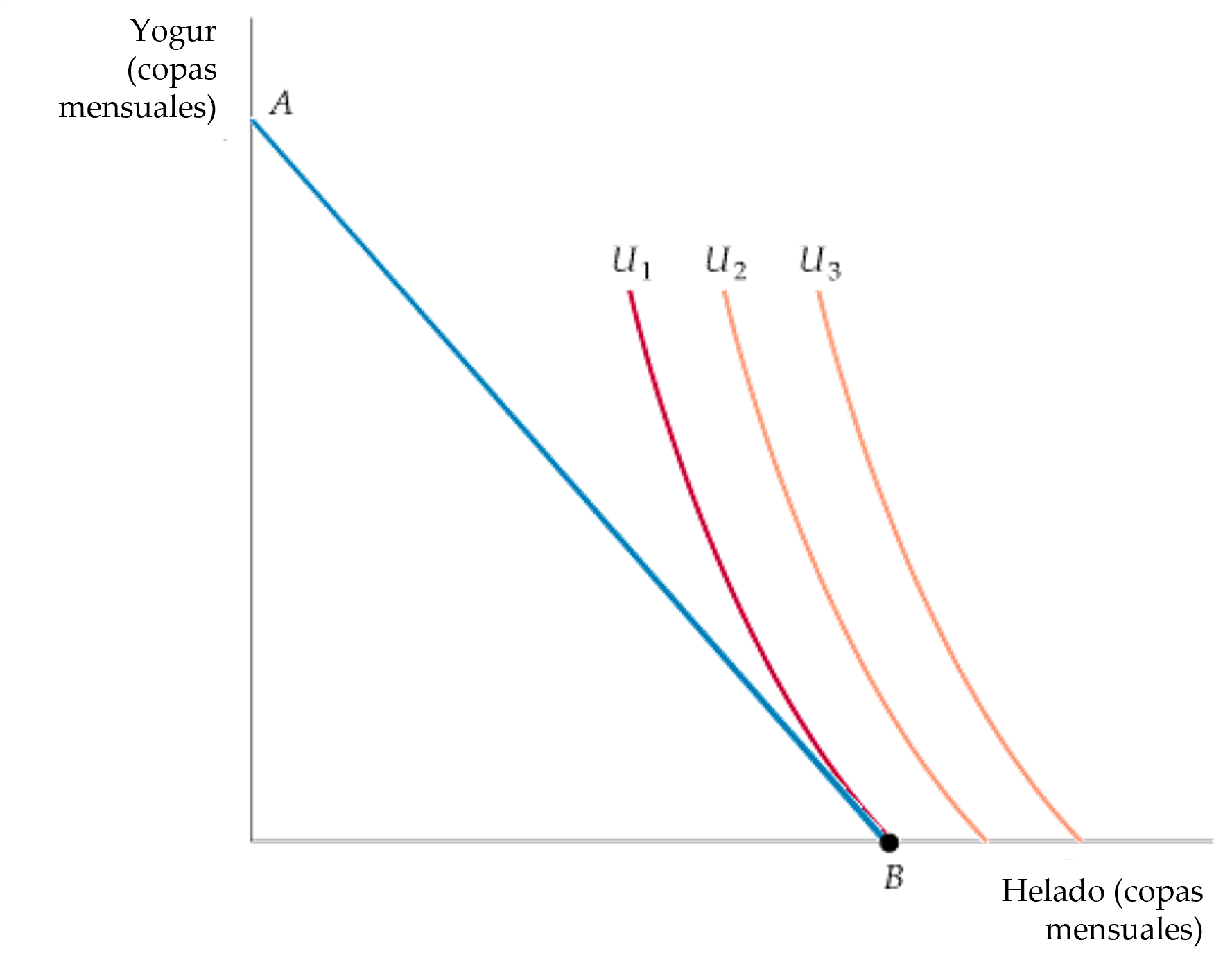
Figura: Soluciones de Esquina

Cuando la relación marginal de sustitución no es igual a la relación de precios correspondiente a todos los niveles de consumo, surge una solución de esquina.
Dada la recta presupuestaria AB, se alcanza el máximo nivel de satisfacción en el punto B de la curva de indiferencia (U_1), donde la RMS (de yogur por helado) es mayor que el cociente entre el precio del helado y el del yogur.

4. Otros temas asociados

La Preferencia Revelada

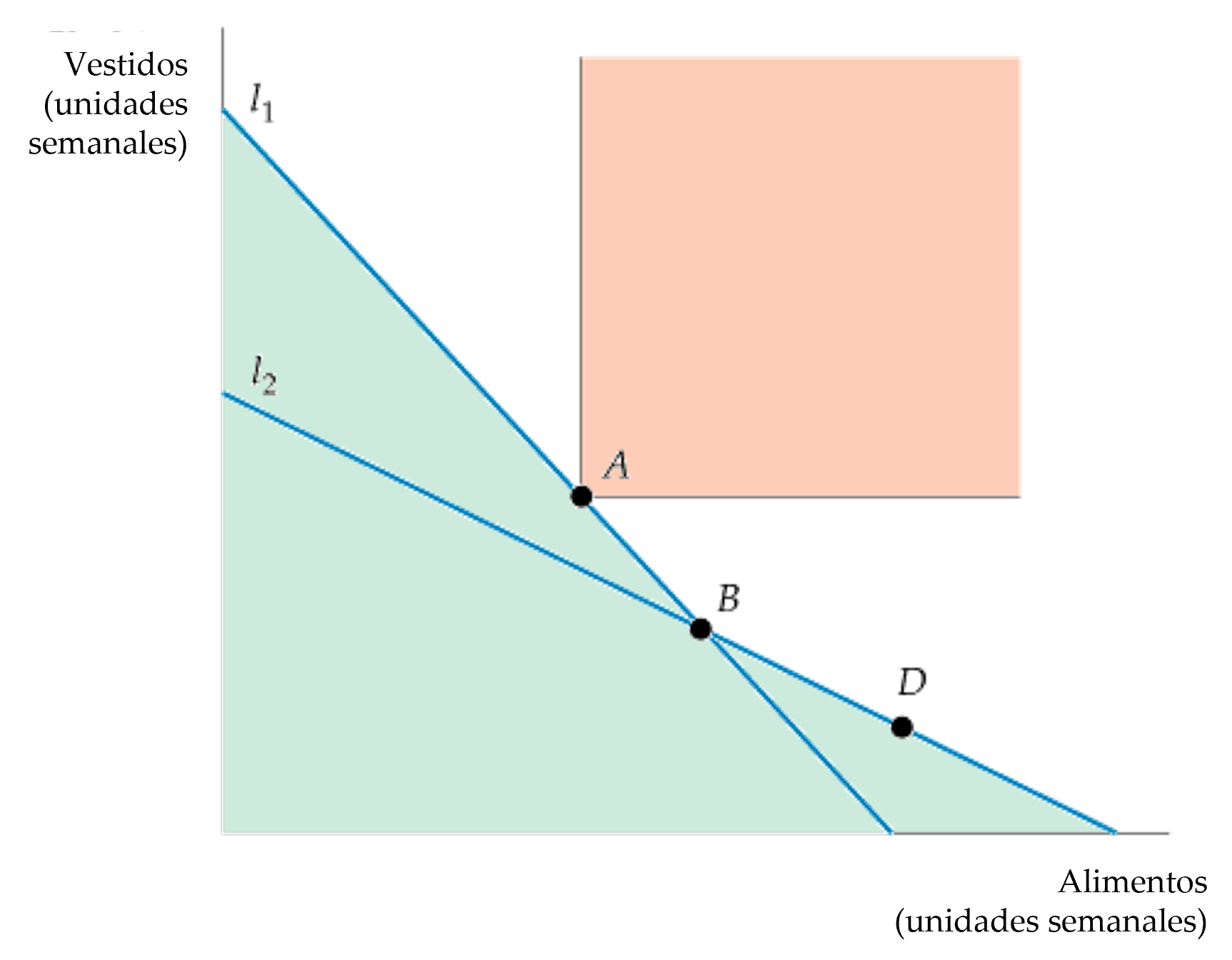
Figura: La Preferencia Revelada

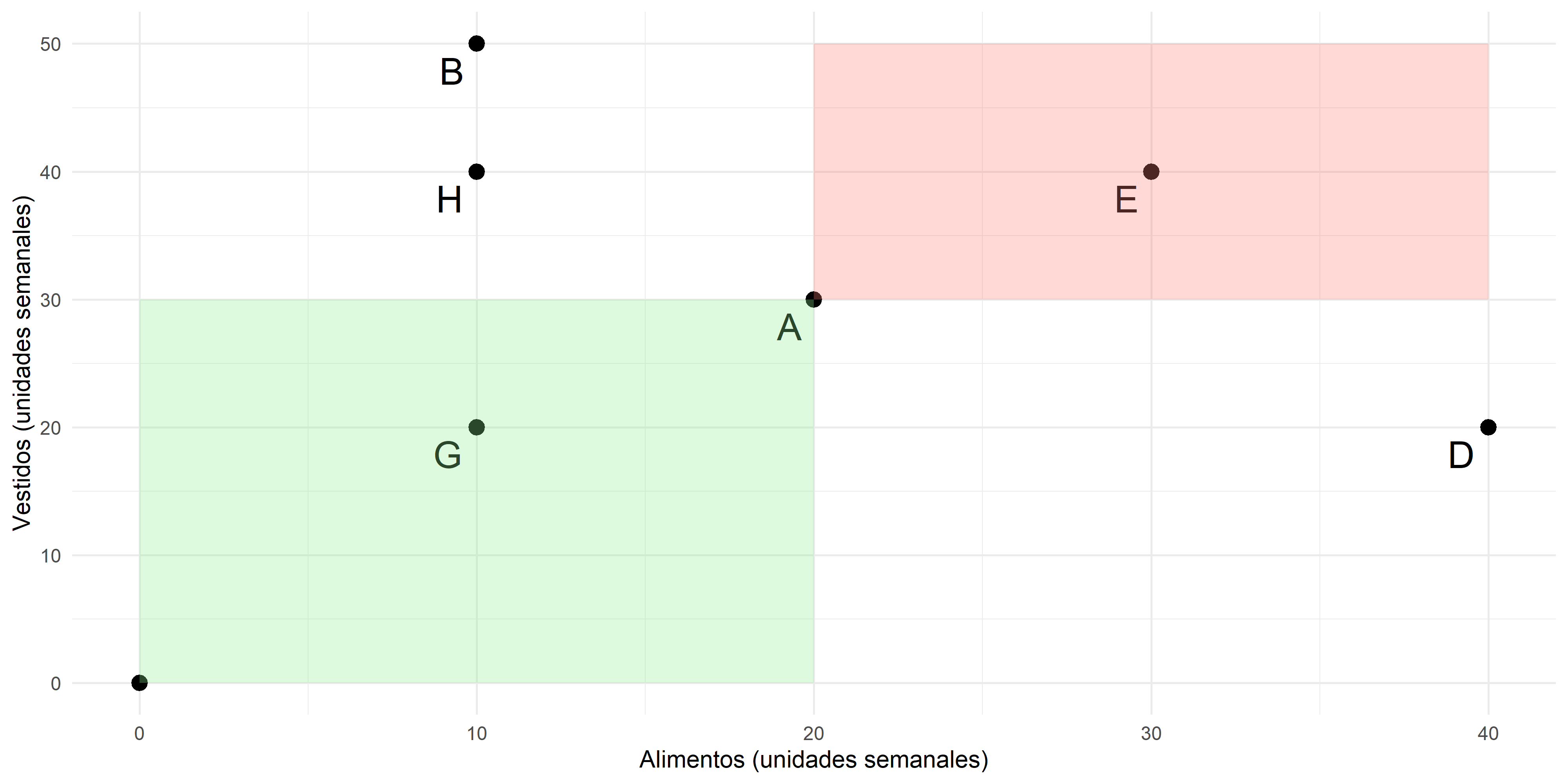
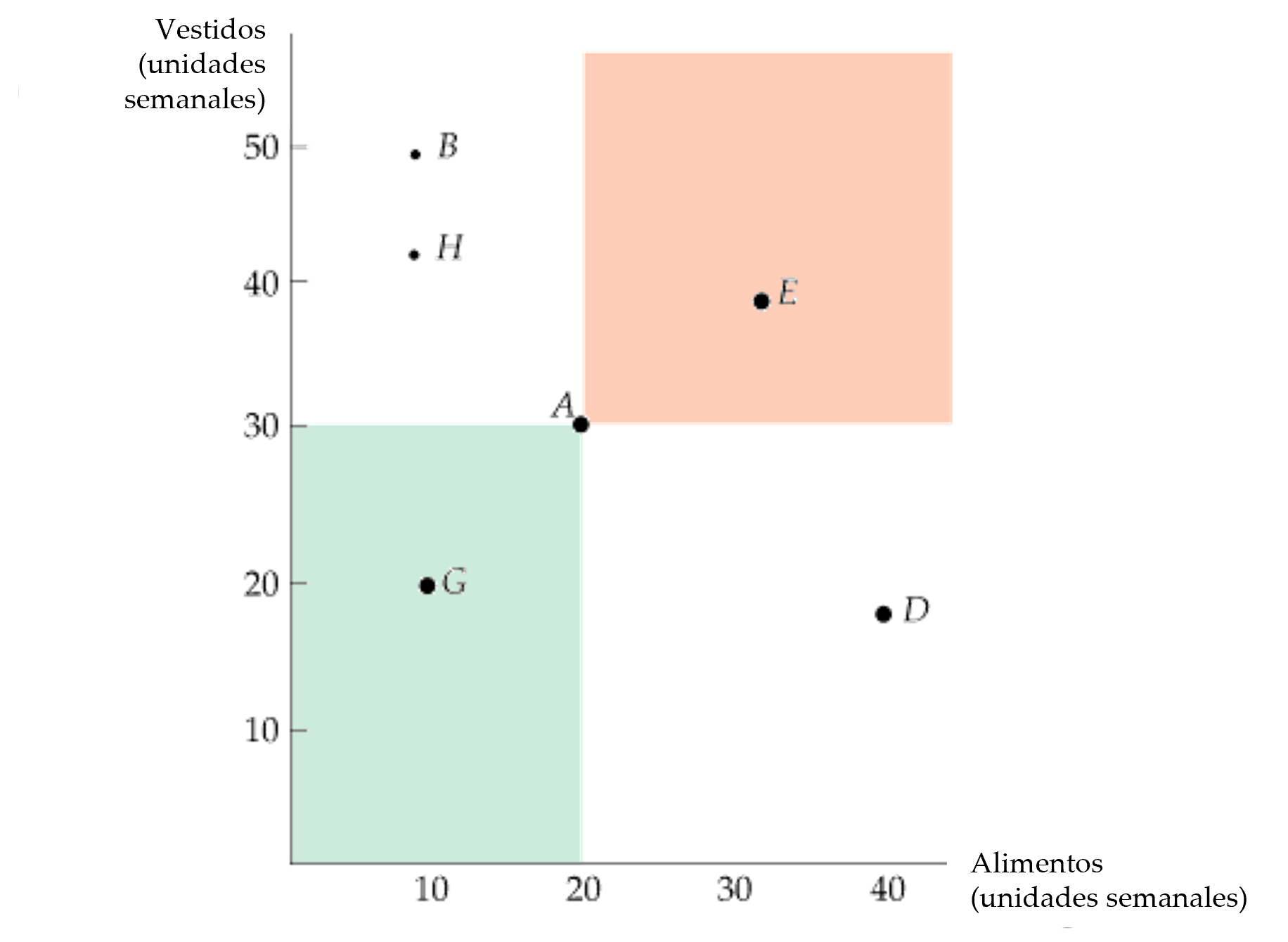
Si una persona que se enfrenta a la recta presupuestaria $l_1$ ha elegido la cesta de mercado A en lugar de la B, revela que prefiere la A a la B.
Asimismo, si ante la recta presupuestaria $l_2$ elige la cesta de mercado B, revela que la prefiere a la D.
Se prefiere A a todas las cestas de mercado del área sombreada de verde, mientras que se prefieren todas las cestas de mercado en el área sombreada de rosa a A.

La Preferencia Revelada con Cuatro Rectas Presupuestarias

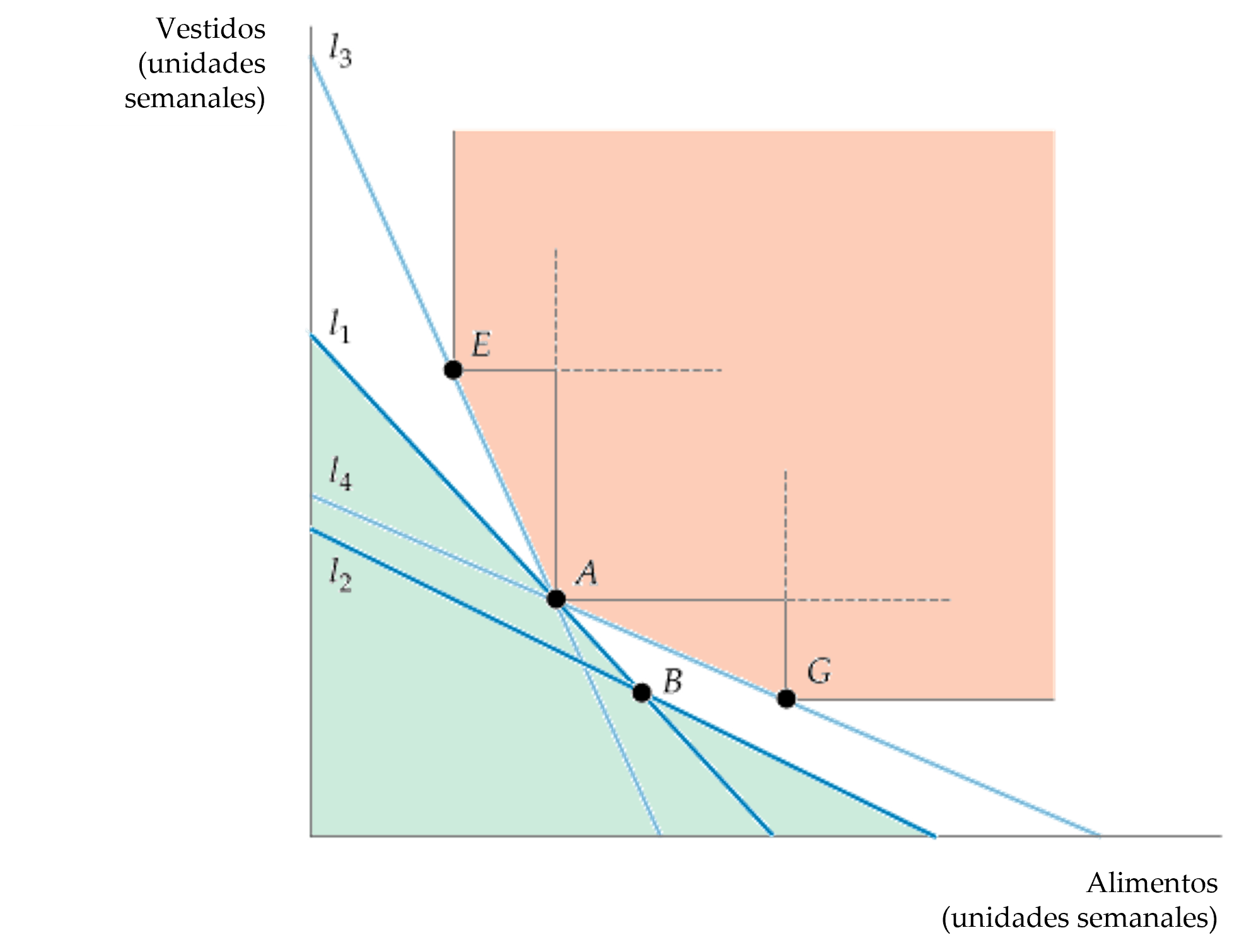
Figura: La Preferencia Revelada con Cuatro Rectas Presupuestarias

Ante la recta presupuestaria $l_3$ , el individuo elige E, lo que revela que la prefiere a A (dado que pudo haber elegido A).
Asimismo, en la recta $l_4$ , el individuo elige G, lo que también revela que la prefiere a A.
Se prefiere A a todas las cestas de mercado en el área sombreada de verde, mientras que se prefieren todas las cestas del área sombreada de rosa a A.

Los índices del costo de la vida

índice del costo de la vida: cociente entre el costo actual de una cesta representativa de bienes y servicios de consume y el costo durante un período base.
índice del costo de la vida ideal: El costo de alcanzar un determinado nivel de utilidad a los precios actuales en relación con el costo de alcanzalo a los años del precio base.
índice de precios Laspeyres Cantidad de dinero a los precios del año actual que necesita una persona para comprar la cesta de bienes y servicios elegida en el año base, dividida por el costo de comprar esa misma cesta a los precios del año base.
índice Paasche Cantidad de dinero a los precios del año actual que necesita una persona para comprar una cesta de bienes y servicios dividida por el costo de comprarla en el año base.
IPC índice de precios al consumidor, es un índice del costo de la vida en el que las cantidades de bienes y servicios ‘no’ varían.

Nota: En mis apuntes para macroeconomía ( fundmacro.luischanci.com ) abordo en más detalle el tema.

Cierre

¿Preguntas?