Producción
(Fundamentos) Microeconomía
Contenidos
- Las empresas y sus decisiones de producción
- La producción con un factor variable (el trabajo)
- La producción con dos factores variables
- Los rendimientos de escala
Producción
La teoría de la empresa explica cómo toma la empresa sus decisiones minimizadoras de los costos y cómo varía su costo con su nivel de producción.
Las decisiones de producción de las empresas son análogas a las decisiones de compra de los consumidores y pueden comprenderse también siguiendo tres pasos:
- Tecnología de Producción
- Restricciones de los Costos
- Elecciones de los factores
Producción
Tecnología de Producción: La Función de Producción
Factores de producción: Factores que intervienen en el proceso de producción (por ejemplo, trabajo \(L\) , capital \(L\) , y materias primas). Los factores y los productos son flujos.
Función de producción: Función que muestra el nivel de producción máximo que puede obtener la empresa con cada combinación específica de factores.
- Representación: sea \(F()\) una función y \(A\) una medida de productividad agregada, \[Y=AF(K,L)\]
- La función de producción describe lo que es técnicamente viable cuando la firma opera eficientemente.
Producción
Tecnología de Producción: La Función de Producción
El corto versus el largo plazo
- Corto plazo: Período de tiempo en que no es posible alterar las cantidades de uno o más factores de producción.
- Factor fijo: Factor de producción que no puede alterarse.
- Largo plazo: Período de tiempo necesario para que todos los factores de producción sean variables.
Producción con un factor variable (el trabajo)
Ejemplo: tabla que ilustra el producto
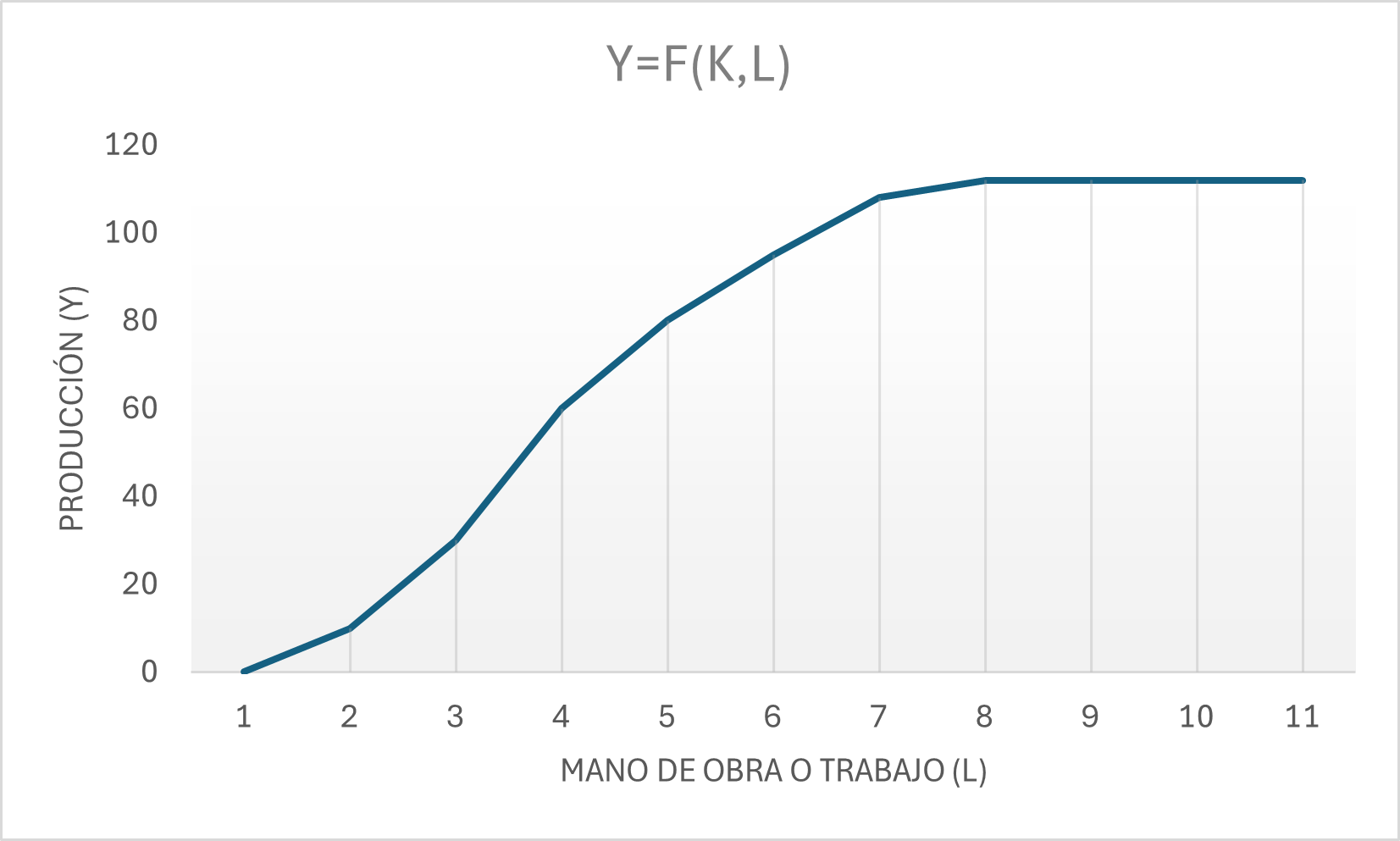
La tabla ilustra como aumenta el producto al ir incrementando los trabajadores.
\[ \begin{array}{|c|c|c|} \hline \textbf{L} & \textbf{K} & \textbf{Y} \\ \hline 0 & 10 & 0 \\ 1 & 10 & 10 \\ 2 & 10 & 30 \\ 3 & 10 & 60 \\ 4 & 10 & 80 \\ 5 & 10 & 95 \\ 6 & 10 & 108,0 \\ 7 & 10 & 110,0 \\ 8 & 10 & 111,0 \\ 9 & 10 & 111,5 \\ 10 & 10 & 111,6 \\ \hline \end{array} \]
\[\,\] 
Producción con un factor variable (el trabajo)
Producto medio: Producto medio por unidad de un determinado factor, \[\text{Producto medio del trabajo}=PMe_{L}=\frac{Producto}{Cantidad de Trabajo}=\frac{Y}{L}=\frac{F(K,L)}{L}\]
Producto marginal: Producción adicional obtenida cuando se incrementa un factor en una unidad \[\text{Producto marginal del trabajo}=PML=\frac{Variación de la producción}{Varaición en la cantidad de trabajo}=\frac{\Delta Y}{\Delta L}\]
Producción con un factor variable (el trabajo)
Ejemplo: producto medio y marginal
\[ \begin{array}{|c|c|c|c|c|} \hline \textbf{L} & \textbf{K} & \textbf{Y} & \textbf{PMeL} & \textbf{PML} \\ \hline 0 & 10 & 0 & - &- \\ 1 & 10 & 10 & 10/1=10&(10-0)/(1-0)=10/1=10 \\ 2 & 10 & 30 & 30/2=15&(30-10)/(2-1)=20/1=20 \\ 3 & 10 & 60 & 20& 30\\ 4 & 10 & 80 & 20& 20\\ 5 & 10 & 95 & 19& 15\\ \hline \end{array} \]
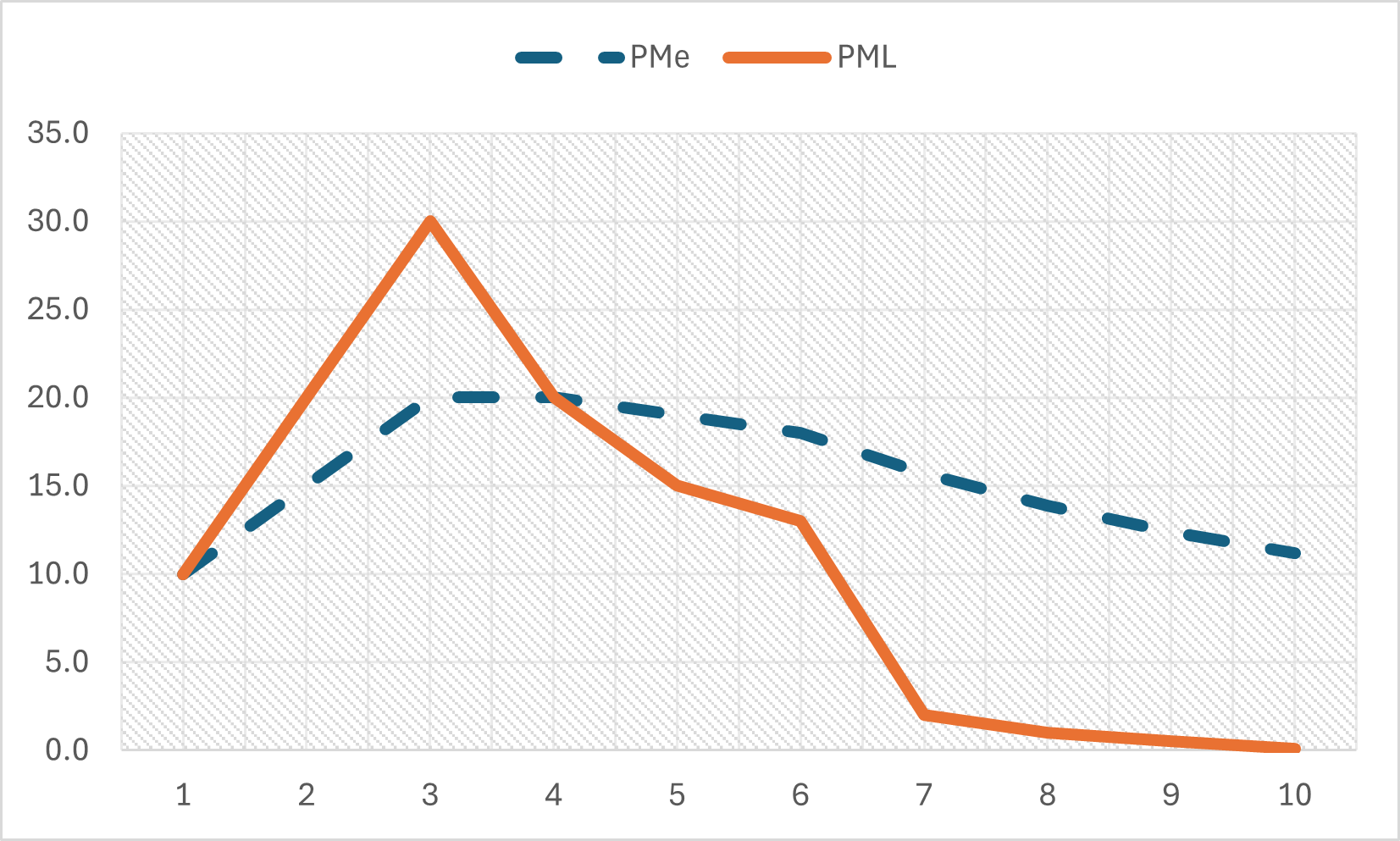
Producción con un factor variable (el trabajo)
Ejemplo. Supongamos una función de producción dada por
\[Y=F(K,L)=K^{1/2}L^{1/2}\]
y que en el corto plazo el capital esta fijo en \(K=\bar{K}=4\).
Las funciones de producción de corto plazo, de producto medio y marginals son
\[Y=(L)=2L^{1/2}\hspace{1cm};\hspace{1cm}PMe=2L^{-1/2}\hspace{1cm};\hspace{1cm}PML\equiv\frac{dY}{d L}=L^{-1/2}\]
Producción con un factor variable (el trabajo)
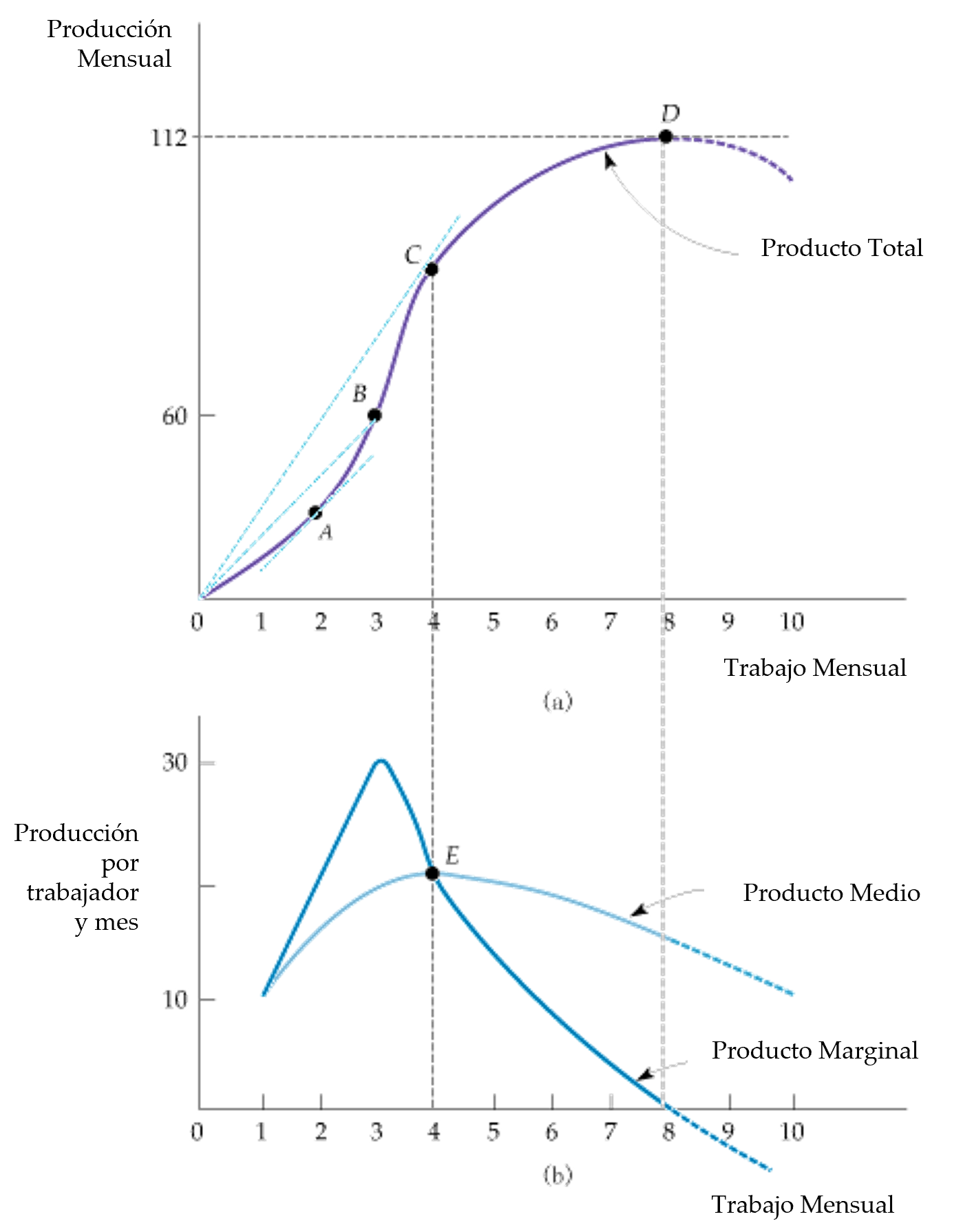
Figura: Producción con un factor variable (L)
- A la izquierda del punto E en (b), el producto marginal es superior al producto medio y el producto medio es creciente; la derecha de E, el producto marginal es inferior al producto medio y éste último es decreciente.
- Por lo tanto, E es el punto en que el producto medio y el producto marginal son iguales y donde el producto marginal alcanza su máximo.
- En D, cuando se maximiza la producción, la pendiente de la tangente de la curva de producción total es 0, como el producto marginal.
Producción con un factor variable (el trabajo)
La ley de los rendimientos marginales decrecientes
Ley de los rendimientos marginales decrecientes: principio según el cual cuando se aumenta el uso de un factor mientras los demás permanecen fijos, la producción adicional obtenida acaba disminuyendo.
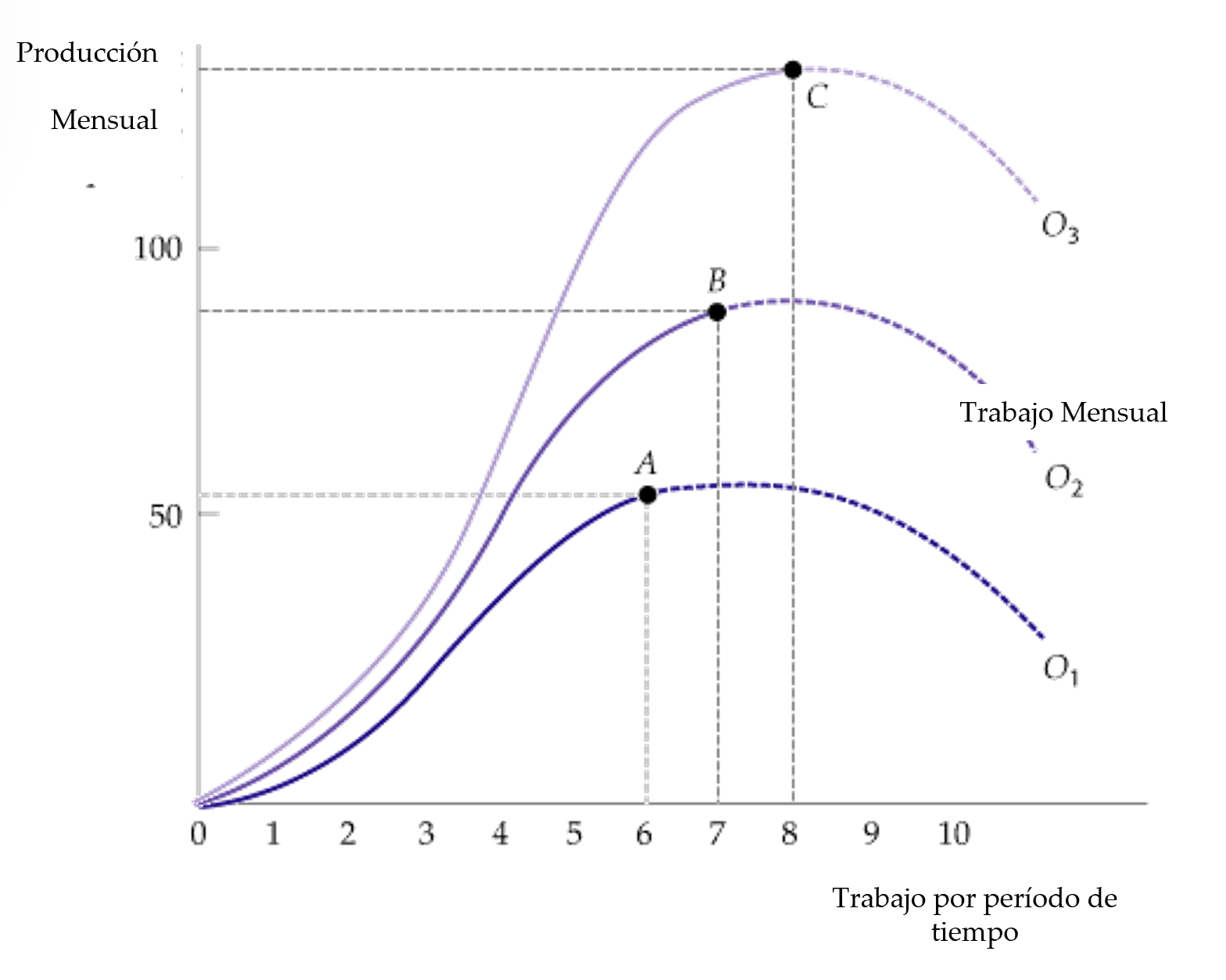
Figura: El efecto de la mejora tecnológica
- La productividad del trabajo (la producción por unidad de trabajo) puede aumentar si mejora la tecnología, incluso aunque los rendimientos del trabajo en un proceso de producción determinado sean decrecientes.
- Cuando nos desplazamos del punto A de la curva \(O_1\) a B en la curva \(O_2\) a C en la curva \(O_3\) con el paso del tiempo, la productividad del trabajo aumenta.
Producción con un factor variable (el trabajo)
Productividad y nivel de vida
- Productividad del trabajo: Producto medio del trabajo de una industria o de la economía en su conjunto.
- Stock de capital: Cantidad total de capital que puede utilizarse para producir.
- Cambio tecnológico: Desarrollo de nuevas tecnologías que permiten utilizar los factores de producción de forma más eficiente.
La producción con dos factores variables
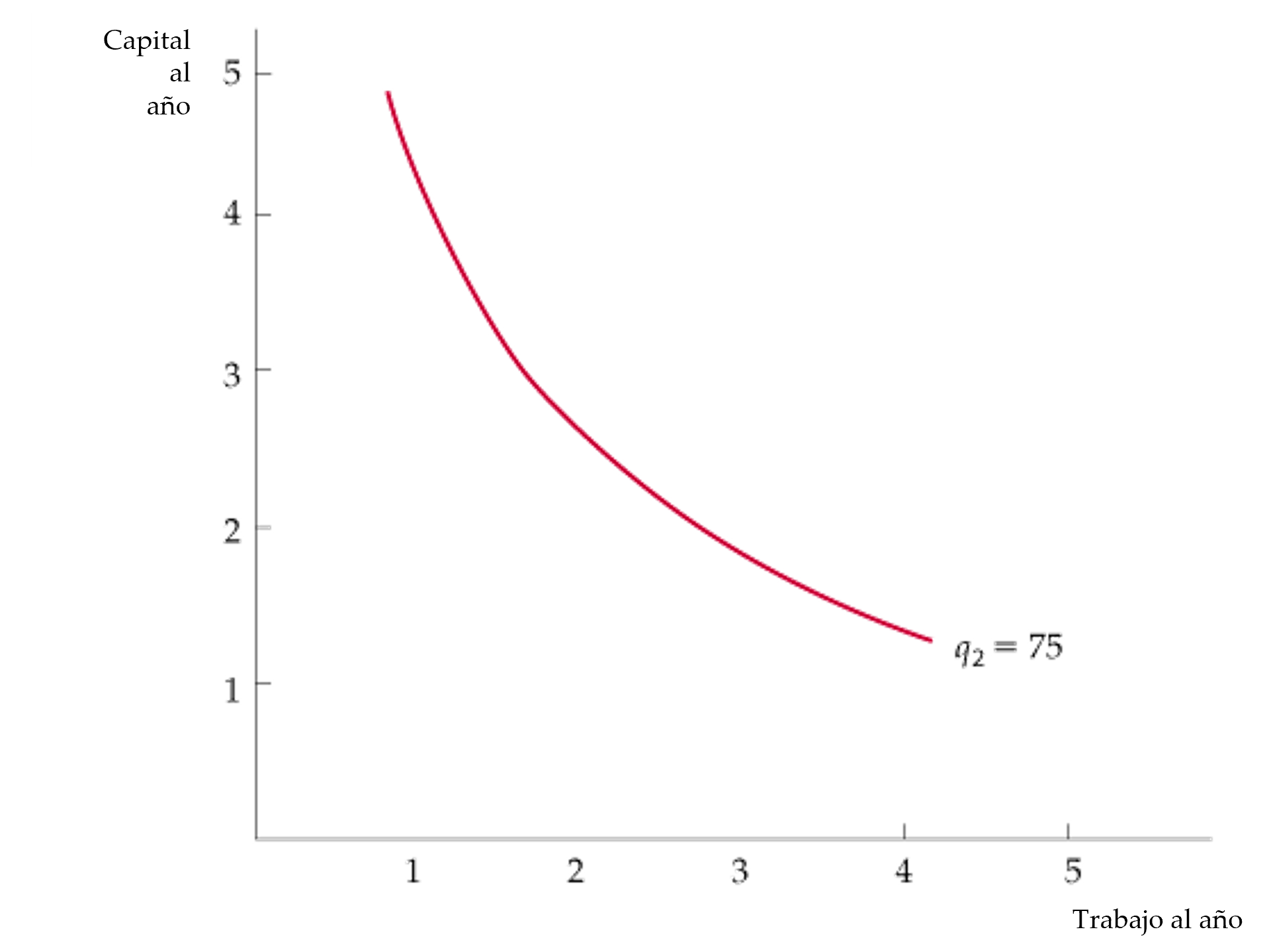
isocuanta: curva que muestra todas las combinaciones posibles de factores que generan el mismo nivel de producción.
Tabla de producción and Figura Isocuanta
\[ \begin{array}{|c|ccccc|} \hline & \textbf{L} & & & & \\ \textbf{K} & 1 &2&3&4&5\\ \hline 1 & 20 &40 &55 &65 &\underline{\textbf{75}} \\ 2 & 40 &60 &\underline{\textbf{75}} &85 &90 \\ 3 & 55 & \underline{\textbf{75}} &90 &100 &105 \\ 4 & 65 & 85&100 &110 &115 \\ 5 & \underline{\textbf{75}} &90 &105 &115 &120 \\ \hline \end{array} \]
La producción con dos factores variables
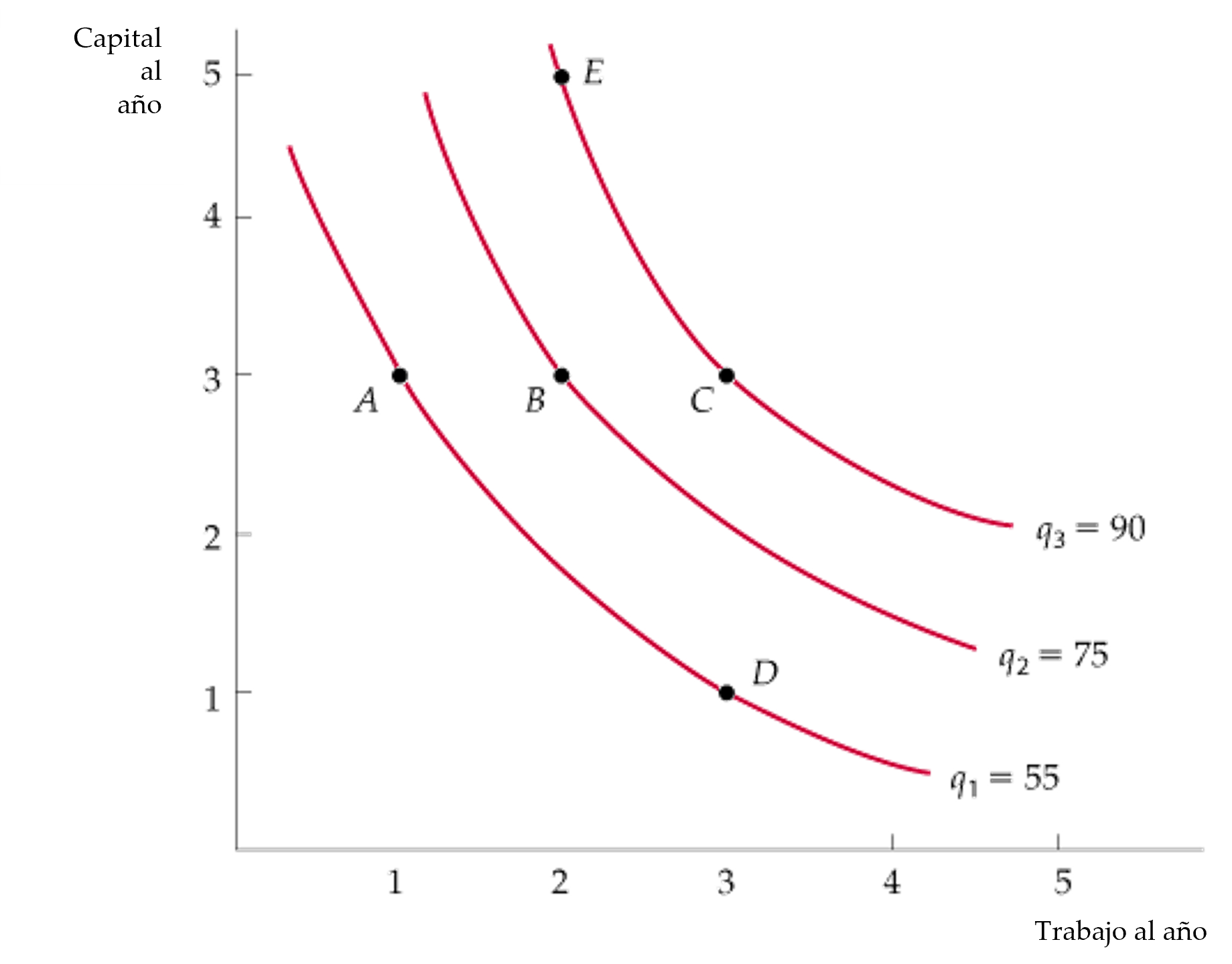
mapa de isocuantas gráfico que muestra varias isocuantas utilizadas para describir una función de producción.
Figura: Differentes Isocuantas
- Las isocuantas de producción muestran las distintas combinaciones de factores necesarias para que la empresa obtenga un determinado nivel de producción. Un conjunto de isocuantas o mapa de isocuantas describe la función de producción de la empresa.
- La producción aumenta a medida que pasamos de la isocuanta \(q_1\) (en la que se producen 55 unidades al año en puntos como el A y D),
- A la isocuanta \(q_2\) (75 unidades por año en el punto B) y la isocuanta \(q_3\) (90 unidades al año en puntos C y E).
La producción con dos factores variables
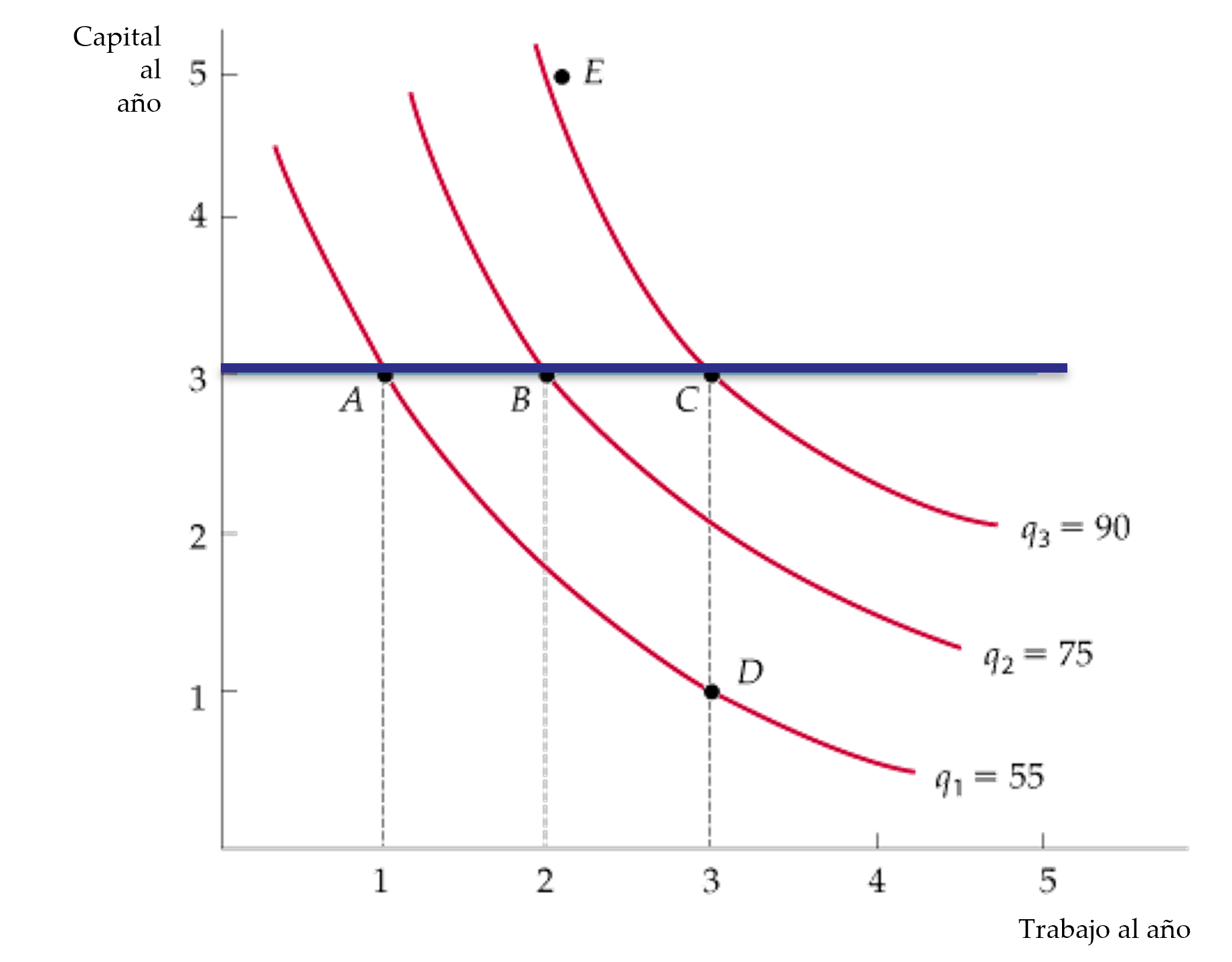
Los rendimientos marginals decrecientes
Figura: Differentes Isocuantas
Los rendimientos marginals decrecientes
Si fijamos el nivel de capital, digamos que en \(K=3\), se observa los niveles de producción de cada isocuanta a medida que se incrementa el trabajo, vemos que cada unidad de trabajo genera una cantidad de producción que aumenta cada vez menor.
La producción con dos factores variables
La sustitución de factores
relación marginal de sustitución técnica (RMST) cantidad en que puede reducirse uno de los factores cuando se utiliza una unidad más de otro, por lo que la producción permanece constante.
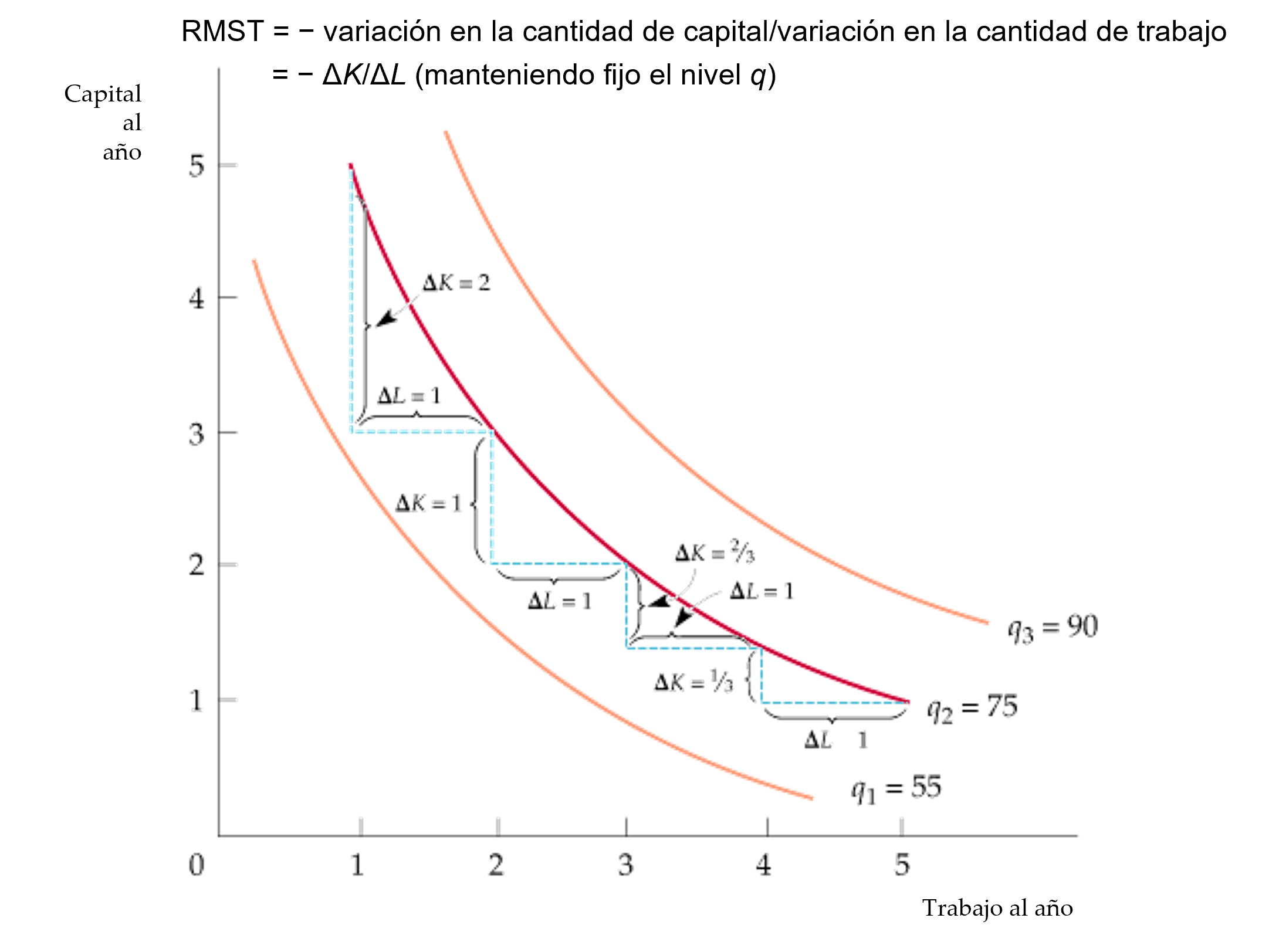
Figura: RMST
- Las isocuantas tienen pendiente negativa y son convexas.
- La pendiente de la isocuanta en un punto cualquiera mide la relación marginal de sustitución técnica —que es la capacidad de la empresa de sustituir capital por trabajo y mantener constante el nivel de producción. \[RMST=\frac{PM_L}{PM_K}=−\frac{\Delta K}{\Delta L}\]
- En la isocuanta q2, la RMST desciende de 2 a 1 y de 2/3 a 1/3.
La producción con dos factores variables
La función de producción – dos casos especiales
Caso 1: (factores) sustitutos perfectos. Capital y mano de obra son intercambiables.
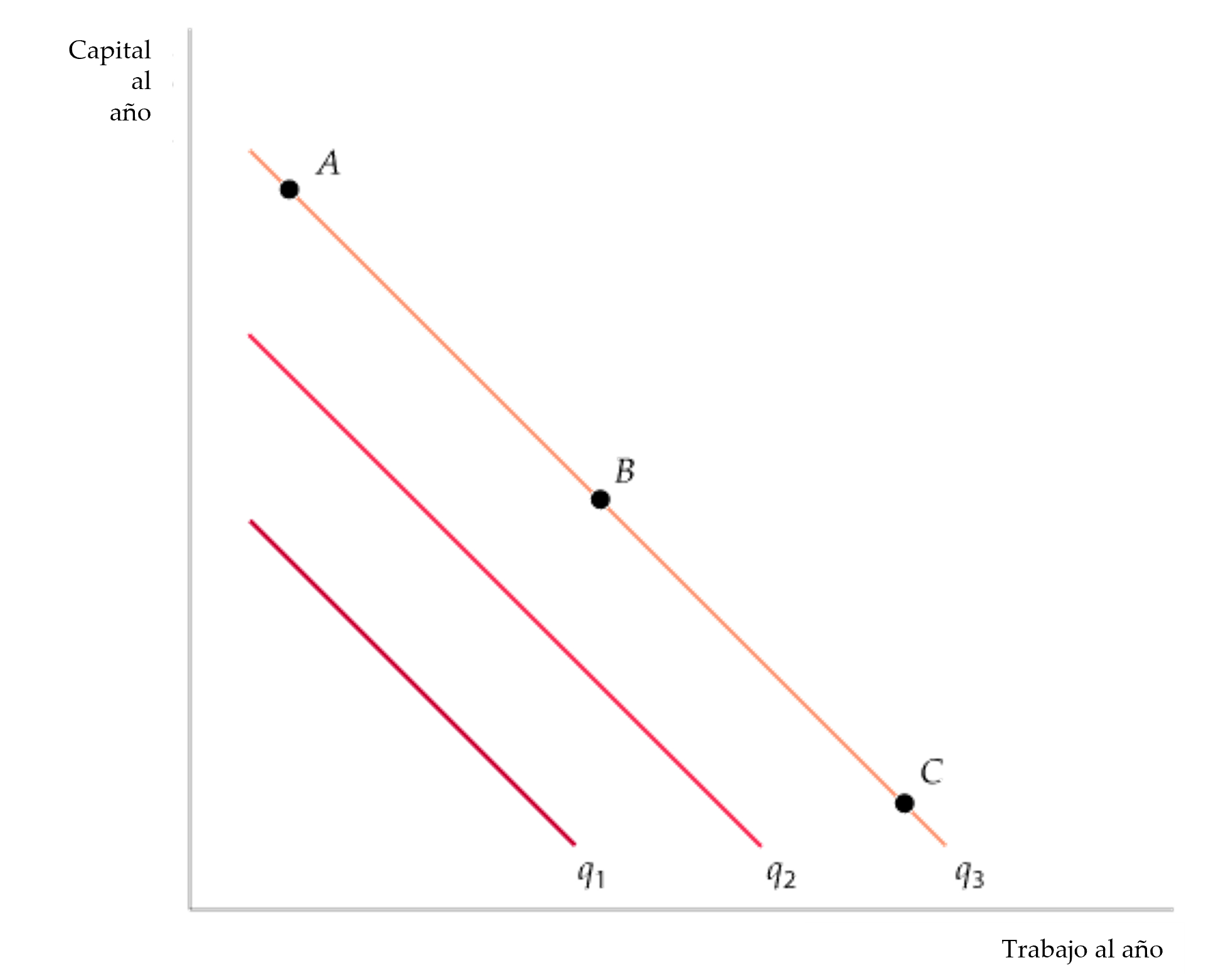
Figura: Las isocuantas cuando los factores son sustitutivos perfectos
- Cuando las isocuantas son líneas rectas, la RMST es constante. Por tanto, la relación a la que pueden sustituirse mutuamente el capital y el trabajo es la misma cualquiera que sea la cantidad de factores que se utilice.
- Los puntos A, B, y C representan tres combinaciones de capital y trabajo que generan el mismo nivel de producción q3.
La producción con dos factores variables
La función de producción – dos casos especiales
Caso 2: (factores) complementos perfectos (proporciones fijas). función de producción en que las isocuantas tienen forma de L, por lo que solo es posible utilizar una combinación de capital y trabajo para obtener cada nivel de producción.
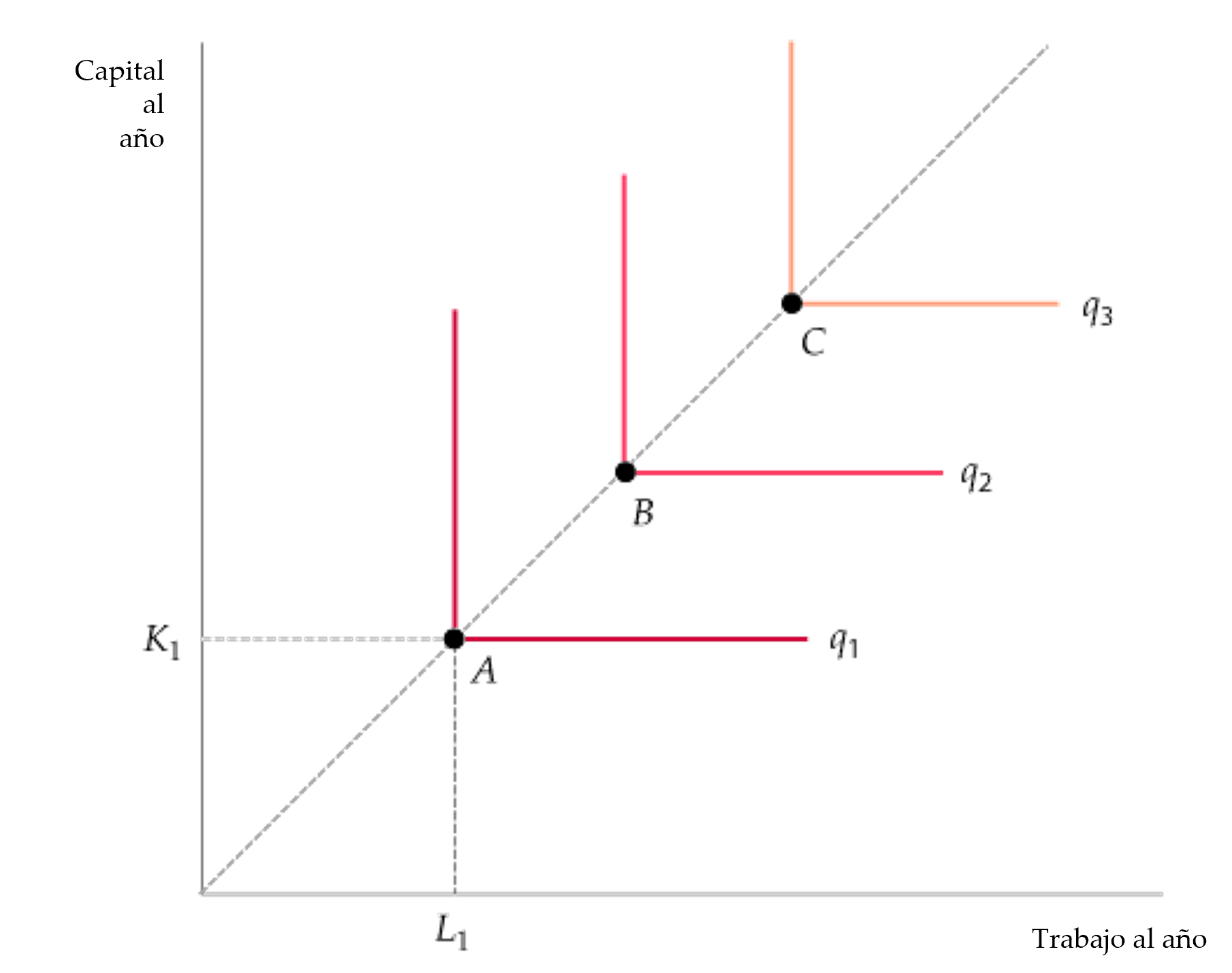
Figura: Las isocuantas cuando los factores son de proporciones fijas
- cuando las isocuantas tienen forma de L, solo puede usarse una combinación de trabajo y capital (como en el punto A de la isocuanta q1, punto B de la isocuanta q2, y punto C de la isocuanta q3). No es posible elevar el nivel de producción utilizando solamente más trabajo o capital.
- La función de producción de proporciones fijas describe situaciones en que los métodos de producción son limitados.
Los rendimientos de escala
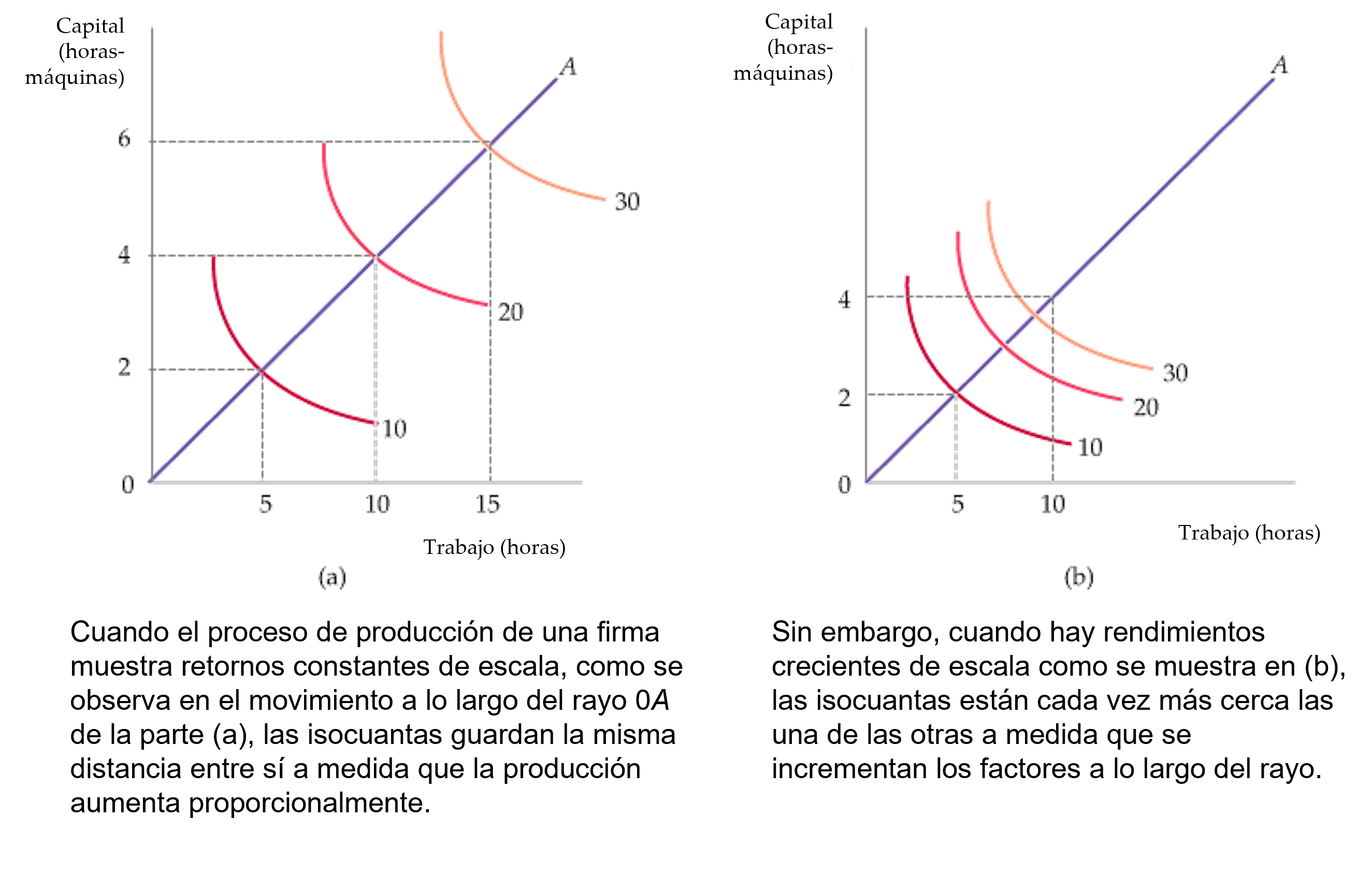
rendimientos de escala: tasa en que se incrementa la producción cuando se incrementan los factores proporcionalmente.
rendimientos crecientes de escala situación en que una duplicación de los factores aumenta más del doble la producción.
rendimientos constante de escala situación en que una duplicación de los factores provoca una duplicación de la producción.
rendimientos decrecientes de escala situación en que una duplicación de los factores provoca un aumento de la producción tal que esta no llega a duplicarse.
Los rendimientos de escala
Los rendimientos de escala
Ejemplo. En las siguientes funciones de producción, \(Y=F(K,L)\), si los factores se duplican (x2), determinar en cuanto varia el producto y concluir respecto a retornos a escala:
\[F(2K,2L)\hspace{0.2cm} vs\hspace{0.2cm}2Y\]
- Caso 1: \(Y=F(K,L)=K^{3/2}L^{1/2}\)
- Caso 2: \(Y=F(K,L)=min\{K,3L\}\)
- Caso 3: \(Y=F(L)=L^{1/2}\)
\(\,\)
Nota: Si desean, para mayor facilidad, pueden reemplazar valores numéricos en \(K\) y \(L\).
Cierre
¿Preguntas?