Costos

(Fundamentos) Microeconomía

Prof. Luis Chancí

Contenidos

1. Introducción: La medición de los costos
2. El costo a corto plazo
3. El costo a largo plazo
4. Las curvas de costo a corto y largo plazo
5. La producción con dos productos —Las economías de alcance
6. Las variaciones dinámicas de los costos —La curva de aprendizaje
7. La estimación y la predicción de costos

1. La medición de los costos

Introducción: La medición de los costos

¿Qué costos son importantes?

• Costo contable vs. Costo económico
  • Costo contable: Gastos efectivos más gastos de depreciación del equipo de capital.
  • Costo económico: costos que tiene una empresa por la utilización de recursos económicos en la producción.
• Costo de oportunidad:
  • Costo de oportunidad: costo correspondiente a las oportunidades que se pierden cuando no se utilizan los recursos de la empresa para el fin para el que tienen más valor.
• costo irrecuperable: Gasto que no puede recuperarse una vez que se realiza.
  • Como no puede recuperarse, no debe influir en las decisiones de la empresa.
  • Como no tiene otro uso, su costo de oportunidad es cero.

Introducción: La medición de los costos

costos fijos y costos variables

• costo fijo (CF): costo que no varía con el nivel de producción y que solo se puede eliminar cerrando.

  • Cerrar no significa necesariamente abandonar el sector.
    • Reducir la producción a cero podría eliminar los costos de materias primas y una gran parte del trabajo.
    • La única manera de eliminar los costos fijos sería cerrar las puertas, apagar la luz y quizás incluso vender o achatarrar la maquinaria.

• costo variable (CV): costo que varía con el nivel de producción, \(CV=C(Q)\).

• costo total (CT o C): costo económico total de producción formado por los costos fijos y los costos variables.

\[CT=CF+CV\]

Introducción: La medición de los costos

¿Qué costos son fijos y cuáles son variables?

• En un horizonte breve (por ejemplo, uno o dos meses), la mayoría de los costos son fijos.
  • En un horizonte breve, una empresa normalmente está obligada a pagar los envíos contratados de materias primas y no puede despedir fácilmente a ningún trabajador.
• En un horizonte más largo (por ejemplo, diez años), casi todos los costos son variables.
  • Es posible despedir a los trabajadores y directivos, y se puede vender o no sustituir una gran parte de la maquinaria cuando se queda obsoleta y se achatarrar.

Amortización de los costos irrecuperables

• Amortización: Política que consiste en tratar un gasto realizado por una vez como un costo anual repartido en una serie de años.
• Los costos irrecuperables son aquellos en los que ha incurrido la empresa y que no pueden recuperarse.
• Un ejemplo es el costo de I+D en que incurre una compañía farmacéutica para desarrollar y probar un nuevo medicamento. Independientemente de que el medicamento sea un éxito o un fracaso, estos costos no pueden recuperarse y, por lo tanto, son irrecuperables.

Introducción: La medición de los costos

El costo marginal y el costo medio

• costo Marginal (CM): Aumento que experimenta el costo cuando se produce una unidad más.
  • Como el costo fijo no varía con el nivel de producción, el costo marginal es el aumento que experimenta el costo variable o el costo total cuando se produce una unidad más.
  • Puede expresarse de la siguiente manera:
  \[ CM = \frac{\Delta CT}{\Delta q}=\frac{\Delta CV}{\Delta q} \]

Introducción: La medición de los costos

El costo marginal y el costo medio

• costo Medio (CM): Costo por unidad de producción. Es decir, costo total de la empresa dividido por su nivel de producción:

  \[CTMe=\frac{CT}{q}\]

• costo fijo medio (CFMe) Costo fijo dividido por el nivel de producción.

• costo variable medio (CVMe) costo variable dividido por el nivel de producción.

Introducción: La medición de los costos

El costo marginal y el costo medio

Nivel de Producción (unidades anuales)	costo Fijo (CF)	costo Variable (CV)	costo Total (CT)	costo Marginal (CM)	costo Fijo Medio (CFMe)	costo Variable Medio (CVMe)	costo Total Medio (CTMe)
0	50	0		–	–	–	–
1	50	50
2	50	78
3	50	98
4	50	112
5	50	130
6	50	150
7	50	175
8	50	204
9	50	242
10	50	300
11	50	385

Introducción: La medición de los costos

El costo marginal y el costo medio

Nivel de Producción (unidades anuales)	costo Fijo (CF)	costo Variable (CV)	costo Total (CT)	costo Marginal (CM)	costo Fijo Medio (CFMe)	costo Variable Medio (CVMe)	costo Total Medio (CTMe)
0	50	0	50	–	–	–	–
1	50	50	100	50	50	50	100
2	50	78	128	28	25	39	64
3	50	98	148	20	16.7	32.7	49.3
4	50	112	162	14	12.5	28	40.5
5	50	130	180	18	10	26	36
6	50	150	200	20	8.3	25	33.3
7	50	175	225	25	7.1	25	32.1
8	50	204	254	29	6.3	25.5	31.8
9	50	242	292	38	5.6	26.9	32.4
10	50	300	350	58	5	30	35
11	50	385	435	85	4.5	35	39.5

2. El costo a corto plazo

El costo a corto plazo

• En el corto plazo hay factores que son (relativamente) más fácil de ajustar.
• Entre el capital (e.g., maquinaria) y la mano de obra (i.e., número de empleados), en el corto plazo, la mano de obra se puede ajustar más rápido que elcapital.
• Por ende, diremos que los salarios que paga una empresa, a corto plazo, son costos variables.
• A largo plazo todo es variable.

El costo a corto plazo

Los determinantes del costo a corto plazo

• La variación del costo variable es el costo unitario del trabajo adicional (w) multiplicado por la cantidad de trabajo adicional necesaria para producir la cantidad adicional (ΔL).
  • Dado que \(\Delta CV = w\cdot\Delta L\) se tiene que:
  \[ CM = \frac{\Delta CV}{\Delta q} = \frac{w\Delta L}{\Delta q} = \frac{w}{PML} \]

Los rendimientos marginales decrecientes y el costo marginal

• La presencia de rendimientos marginales decrecientes significa que el producto marginal del trabajo disminuye cuando aumenta la cantidad de trabajo empleada.
• Como consecuencia, cuando hay rendimientos marginales decrecientes, el costo marginal aumenta cuando aumenta la producción.

El costo a corto plazo

Las formas de las curvas de costos

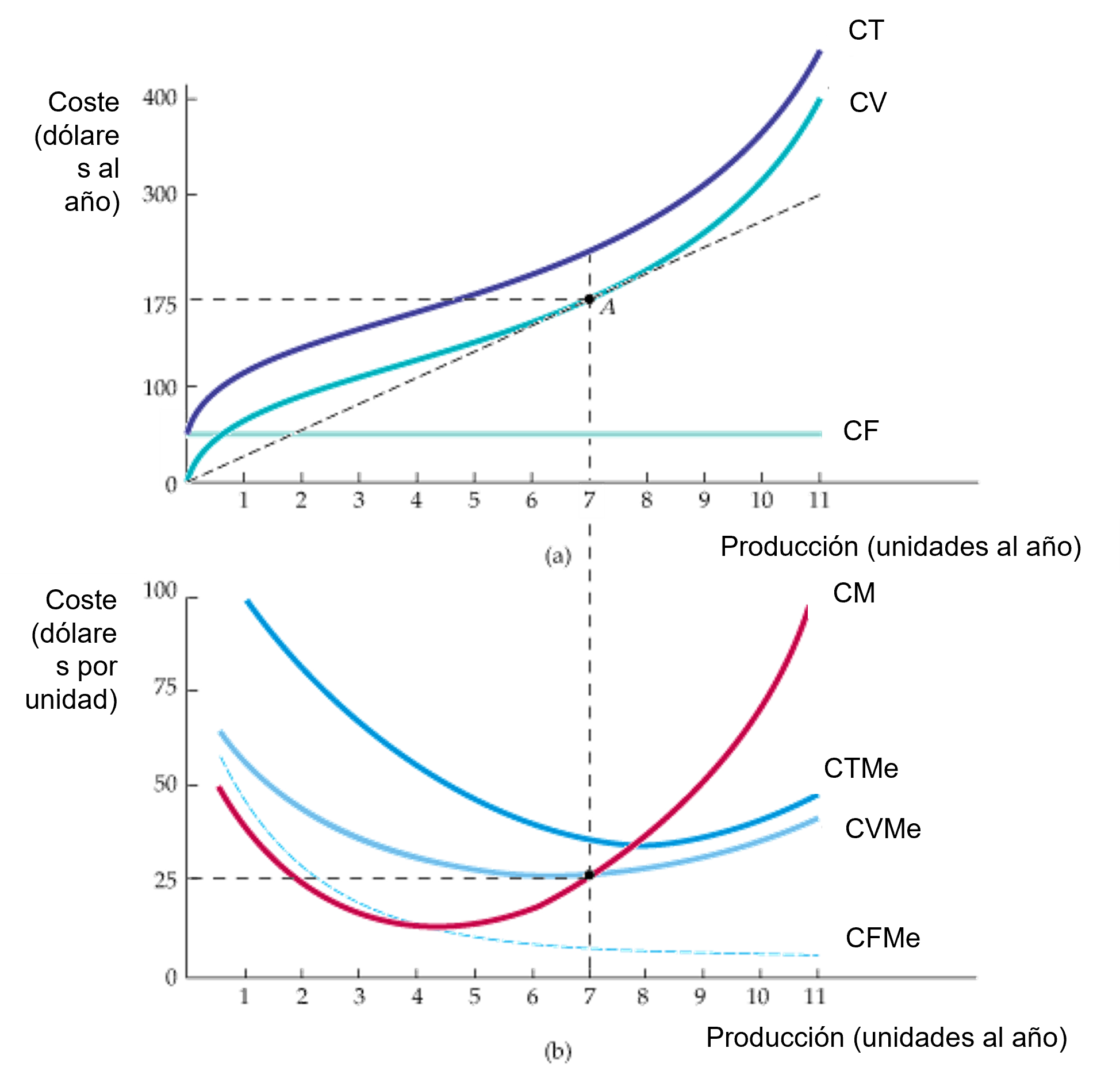
Figura: Las formas de las curvas de costos

Las curvas de costos de la empresa

• En (a) el costo total (CT) es la suma vertical del costo fijo (CF) y el costo variable (CV).
• En (b) el costo total medio (CTMe) es la suma del costo variable medio (CVMe) y el costo fijo medio (CFMe).
• El costo marginal (CM) corta las curvas de costo variable medio y de costo total medio en sus puntos mínimos.

El costo a corto plazo

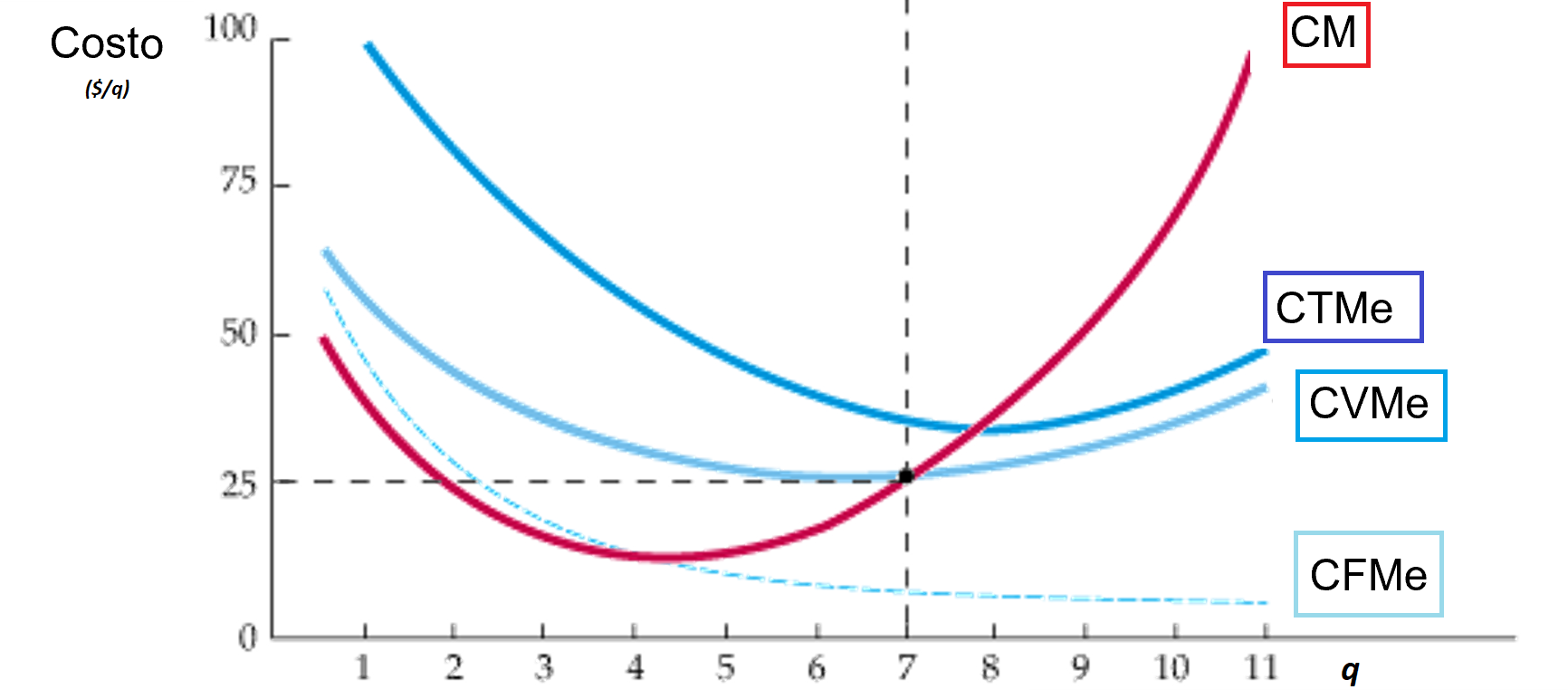
Formas de las curvas: cada una es única y se pueden identificar

\(\,\)

El costo a corto plazo

Las formas de las curvas de costos

La relación medio-marginal

• El costo marginal y el costo medio son otro ejemplo de la relación entre los conceptos de producto medio y producto marginal.

El costo total como un flujo

• El costo total es un flujo, por ejemplo, un determinado número de unidades monetarias al año. Para simplificar el análisis, a menudo omitimos la referencia temporal y nos referimos al costo total en unidades monetarias y a la producción en unidades.

3. El costo a largo plazo

El costo a largo plazo

• En el largo plazo se deja de considerar el capital como fijo.

• El costo del uso del capital

  • Costo del uso del capital: Costo anual de poseer y utilizar un activo de capital igual a la depreciación económica más los intereses perdidos.
  • El costo del uso del capital es la suma de la depreciación económica y los intereses (es decir, el rendimiento financiero) que se podrían haber obtenido si el dinero se hubiera invertido de otra forma. En términos formales:

  \[ \text{Costo de uso del capital} = \text{Depreciación económica} + (\text{Tipo de interés}) \times (\text{Valor del capital}) \]

  \[ r = \text{Tasa de depreciación} + \text{Tipo de interés} \]

• Tasa de alquiler del capital

  • Tasa de alquiler: Costo anual de alquilar una unidad de capital.
  • En un mercado competitivo, la tasa de alquiler debe ser igual al costo de uso (r).

El costo a largo plazo

La elección de los factores que minimizan los costos

• Las firmas deben seleccionar los factores para obtener un determinado nivel de producción con el menor costo posible.

• Utilizamos dos factores variables: trabajo (medido en horas de trabajo al año) y capital (medido en horas de uso de maquinaria al año).

• Recta isocosto: Gráfico que muestra todas las combinaciones de trabajo y capital que pueden comprarse con un costo total dado.

  \[C = wL + rK\]

  • Si reformulamos la ecuación de costo total como la ecuación correspondiente a una línea recta, tenemos que \(K=C/r-(w/r)L\). Así, la recta isocosto tiene, pues, una pendiente de \(\Delta K/\Delta L = −(w/r)\), que es el cociente entre el salario y el costo de alquiler del capital.

El costo a largo plazo

La recta de isocosto

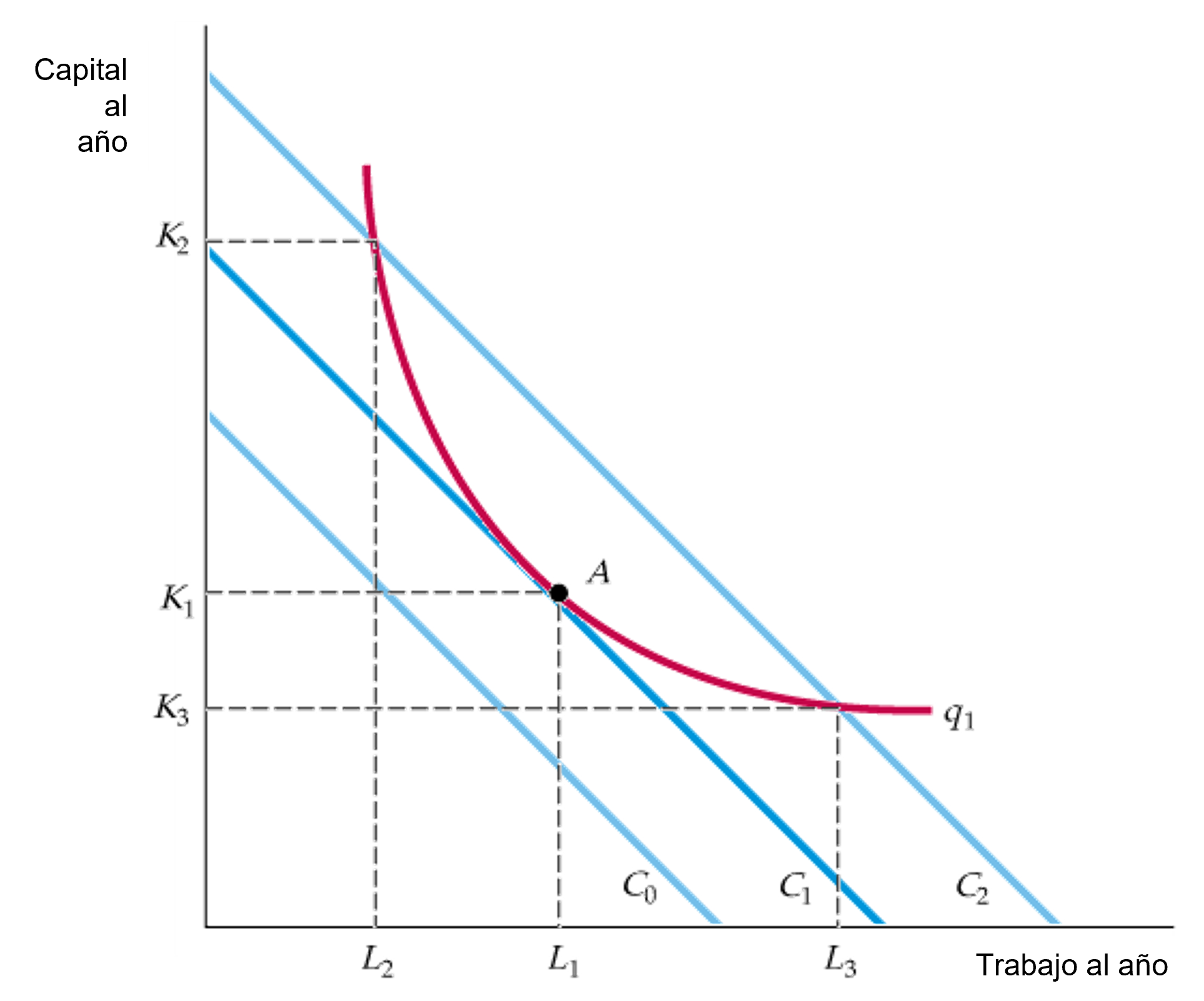
Figura: La obtención de un determinado nivel de produción con costo mínimo

• Las curvas isocostos describen la combinación de factores de producción que cuestan lo mismo a la empresa.
• La curva isocosto \(C_1\) es tangente a la isocuanta \(q_1\) en el punto A y muestra que el nivel de producción \(q_1\) puede obtenerse con un costo mínimo con la cantidad de trabajo \(L_1\) y la cantidad de capital \(K_1\).

El costo a largo plazo

La sustitución de factores

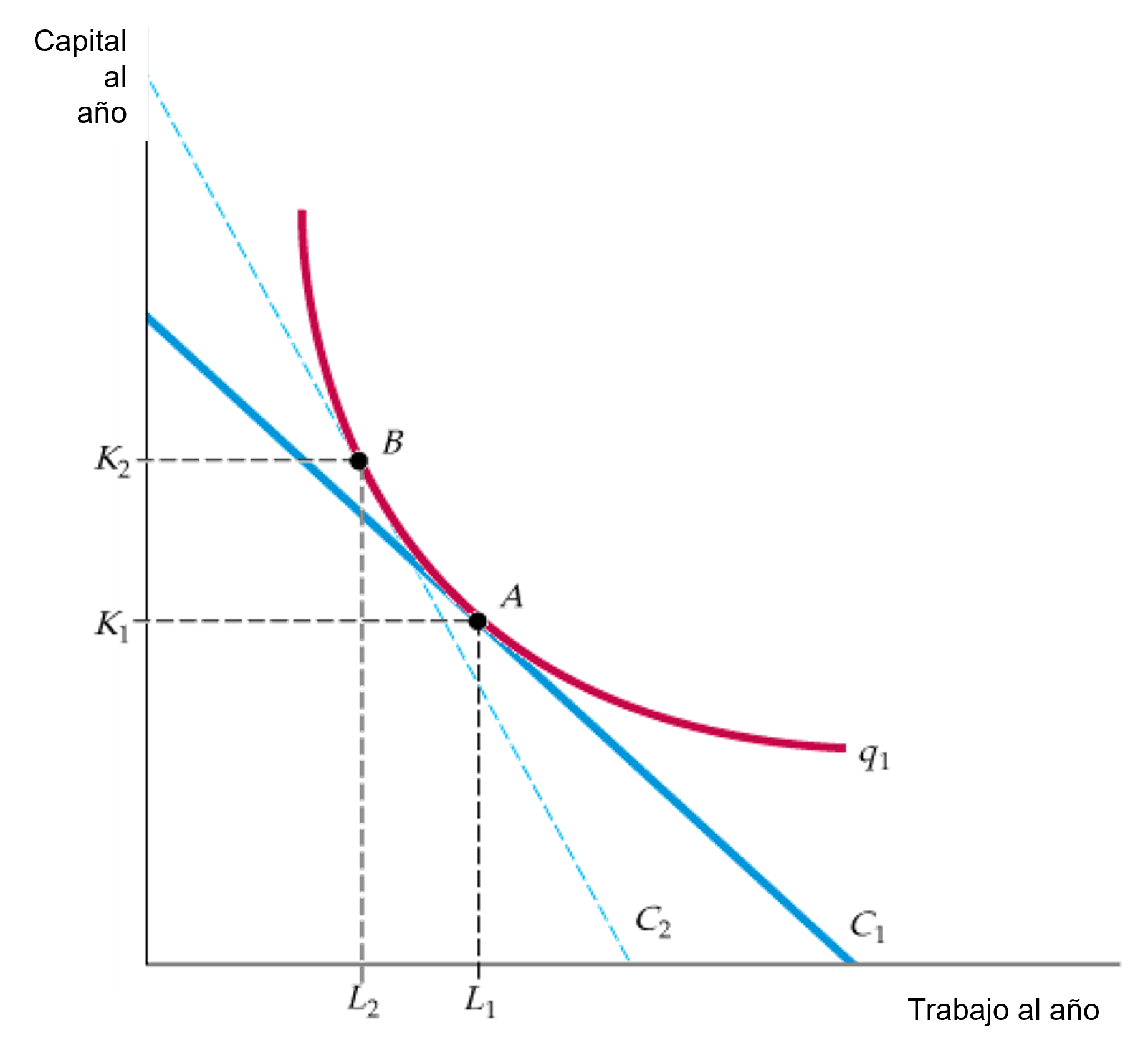
Figura: La sustitución de factores

• Cuando sube el precio del trabajo, las curvas isocosto se vuelven más inclinadas.
• El nivel de producción \(q_1\) se obtiene en el punto B de la curva isocosto \(C_2\) utilizando \(L_2\) unidades de trabajo y \(K_2\) de capital.

El costo a largo plazo

La minimización de costos y la RMST

• La relación marginal de sustitución técnica (RMST) de capital por trabajo es la negativa de la pendiente de la isocuanta y es igual al cociente entre los productos marginales del trabajo y el capital:

\[ \text{RMST} = -\frac{\Delta K}{\Delta L} = \frac{PML}{PMK} \]

• Por lo tanto, cuando una empresa minimiza el costo de producir una determinada cantidad, se cumple la siguiente condición:

\[ \frac{PML}{PMK} = \frac{w}{r} \] - Reordenando levemente esta condición:

\[ \frac{PML}{w} = \frac{PMK}{r} \] en el óptimo, el beneficio obtenido al aumentar una unidad de un factor de producción (productividad marginal) es el mismo para todos los factores, una vez ajustados por sus respectivos precios.

El costo a largo plazo

La senda de expansión y el costo total a largo plazo

Senda de expansión: Curva que pasa por los puntos de tangencia de las rectas isocosto de una empresa y sus isocuantas.

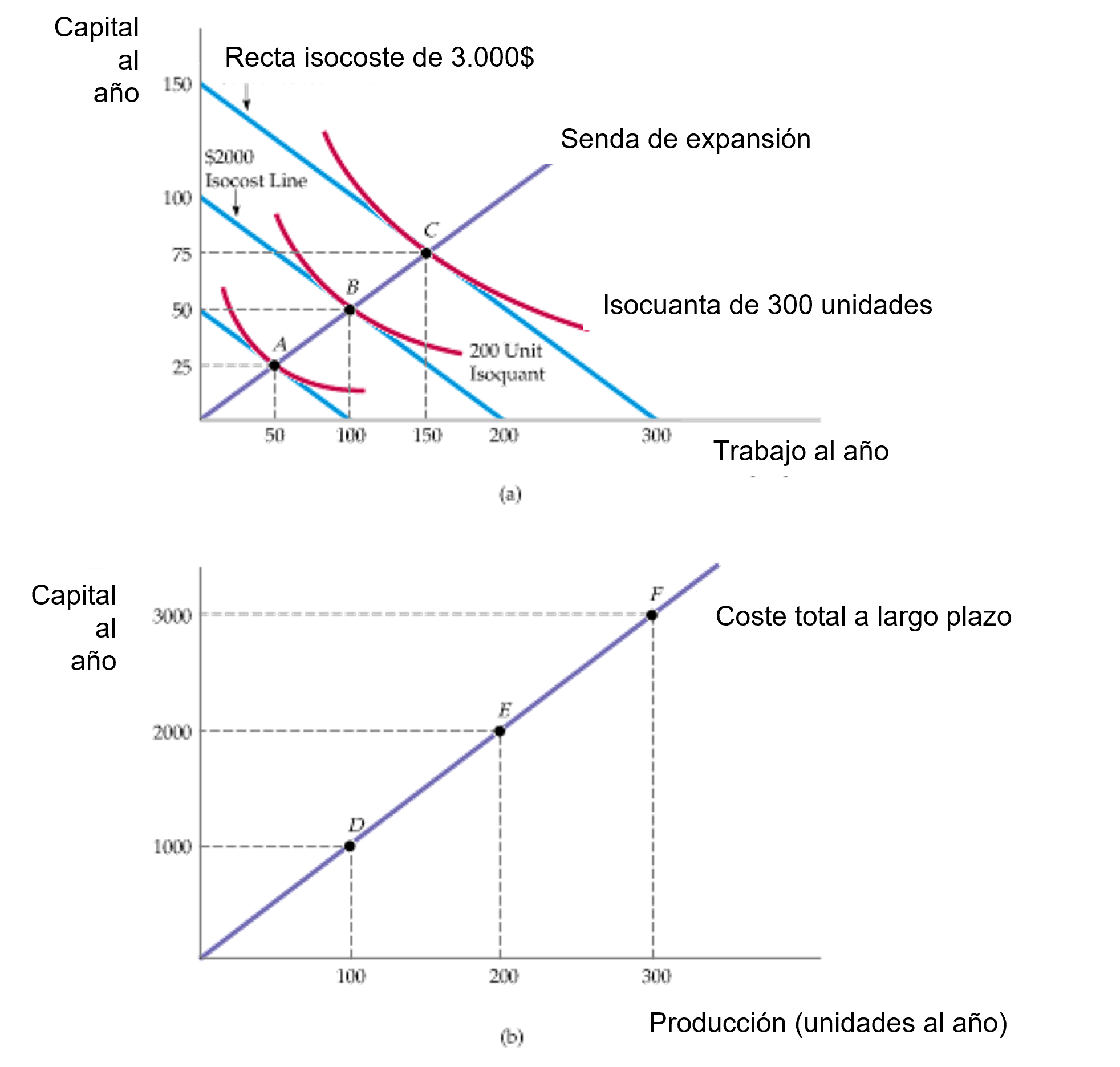
Figura: Senda de expansión y el costo total a largo plazo

En (a) la senda de expansión que parte del origen (y que pasa por los puntos A, B y C) muestra las combinaciones de trabajo y capital de menor costo que pueden utilizarse para obtener cada nivel de producción a largo plazo, es decir, cuando es posible alterar ambos factores de producción.

En (b) la curva de costo total a largo plazo correspondiente (que parte del origen y que pasa por los puntos D, E y F) mide el costo mínimo para obtener cada nivel de producción.

4. Las curvas a corto y largo plazo

Las curvas a corto y largo plazo

La rigidez de la producción a corto plazo

Cuando una empresa produce a corto plazo, puede no minimizar su costo de producción debido a la rigidez en el uso del capital.

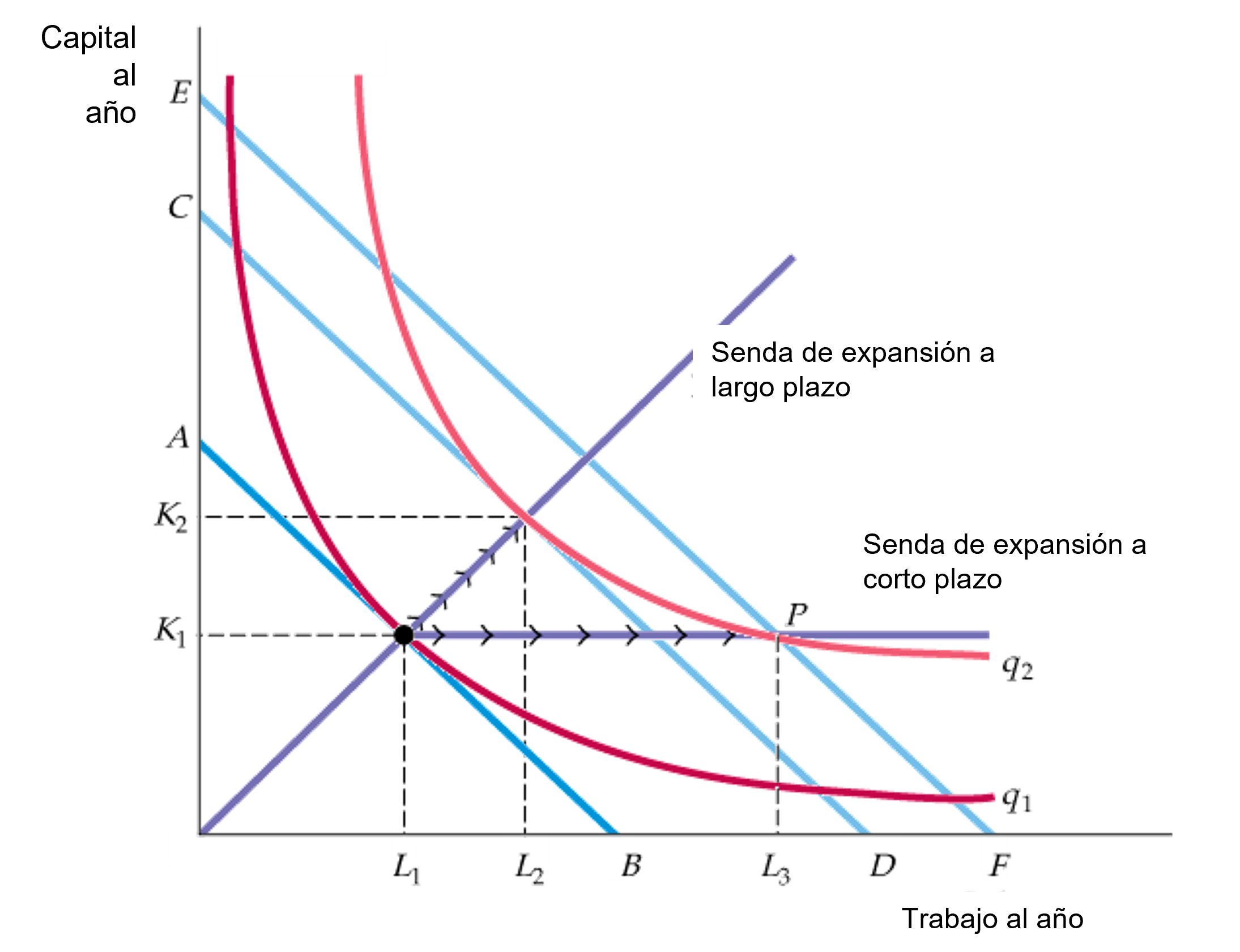
Figura: La rigidez de la producción a corto plazo

El nivel de producción inicial es \(q_1\). A corto plazo, solo se puede producir el nivel \(q_2\) elevando la cantidad de trabajo de \(L_1\) a \(L_3\) ya que el capital se mantiene fijo en \(K_1\). A largo plazo, puede obtener el mismo nivel de producción de un modo más barato elevando la cantidad de trabajo de \(L_1\) a \(L_2\) y la de capital de \(K_1\) a \(K_2\).

Las curvas a corto y largo plazo

Ejemplo

Sea una función de producción \(Y=F(K,L)=K^{1/2}L^{1/2}\), con funciones de productividad marginal:
\[PM_K=(1/2)K^{-1/2}L^{1/2}\hspace{2cm}y\hspace{2cm} PM_L=(1/2)K^{1/2}L^{-1/2}\]

Además, los precios de la mano de obra son \(w=2\) y del capital \(1\). Si la empresa desea producir una cantidad \(Y=20\sqrt{2}\), encontrar los costos totales en los siguientes dos casos:

• Corto plazo: el capital se encuentra fijo en \(\bar{K}=20\).
• Largo plazo: tanto capital \(K\) como mano de obra \(L\) son variables.

Las curvas a corto y largo plazo

Ejemplo (respuesta)

• Corto plazo: si el capital se encuentra fijo en \(\bar{K}=20\), al reemplazar en \(Y=20\sqrt{2}=F(K,L)=K^{1/2}L^{1/2}=20^{1/2}L^{1/2}\), se obtiene \(L=40\). Por ende, el costo total en el corto plazo es \[C_{cp}=2\cdot40+1\cdot20=100\]
• Largo plazo: Si la empresa desea producir \(20\sqrt{2}=K^{1/2}L^{1/2}\), puede ajustar capital y trabajo a una elección óptima dada por \(|RMST_{K,L}|=|r/w|\). Es decir, \[\frac{(1/2)K^{-1/2}L^{1/2}}{(1/2)K^{1/2}L^{-1/2}}=\frac{1}{2}\hspace{0.4cm}\Rightarrow\hspace{0.4cm}K=2L\] Al resolver \(20\sqrt{2}=K^{1/2}L^{1/2}\) y \(K=2L\) se obtiene \(L=20\) y \(K=40\). Por ende, el costo total en el largo plazo es \[C_{lp}=2\cdot20+1\cdot40=60\]

Las curvas a corto y largo plazo

Ejemplo (respuesta)

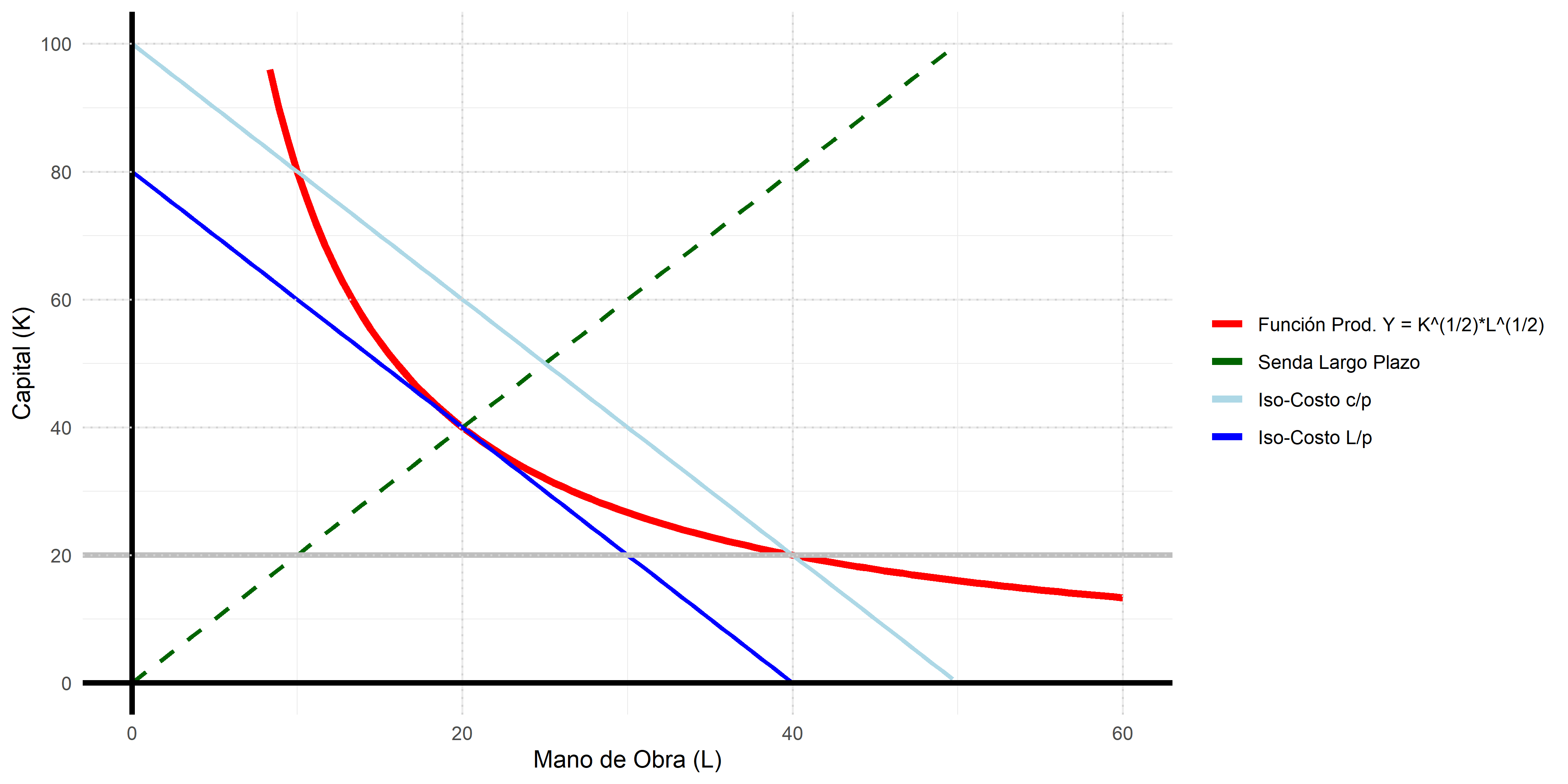
Las curvas a corto y largo plazo

El costo medio y marginal a largo plazo

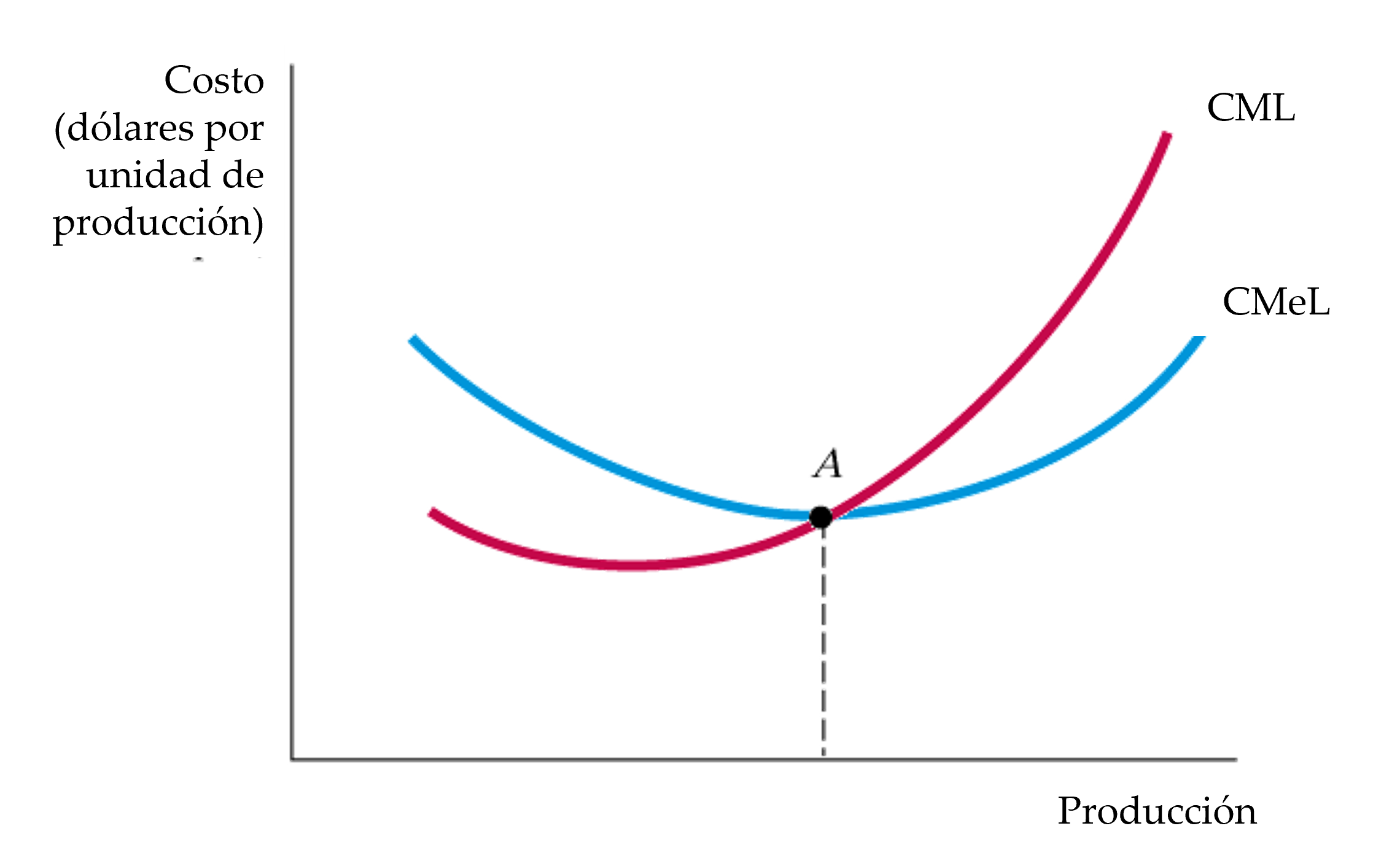
Figura: El costo medio y marginal a largo plazo

Las dos curvas se cortan en el punto A, en el que la curva \(CMeL\) logra su mínimo.

• Cuando una empresa produce en un nivel de producción en el que el costo medio a largo plazo \(CMeL\) es decreciente, el costo marginal a largo plazo \(CML\) es menor que el \(CMeL\).

• En cambio, cuando \(CMeL\) es creciente, el \(CML\) es mayor que el \(CMeL\).

Las curvas a corto y largo plazo

Ejemplo

Llamemos a la cantidad que se produce \(Y\) simplemente \(q\) (de quantity). Sea una función de costos total dada por

\[C=100+2q+q2\]

Las curvas asociadas de costo marginal (CM) y medio (CMe) son \(CM=2+2q\) y \(CMe=2+q+100/q\).

La cantidad \(q\) asociada al mínimo CMe se puede obtener a partir de resolver:

\[2+2q=2+q+\frac{100}{q}\] es decir,

\[q=10\]

Las curvas a corto y largo plazo

Economías y deseconomías de escala

Cuando aumenta la producción, es probable que el costo medio de producción de la empresa disminuya, al menos hasta cierto punto.

• Si la empresa produce en mayor escala, los trabajadores pueden especializarse en lo que son más productivos.
• La escala puede dar flexibilidad. Modificando la combinación de factores utilizados para producir el producto de la empresa, los directivos pueden organizar el proceso de producción más eficazmente.
• La empresa puede adquirir algunos factores de producción con un costo más bajo, ya que los compra en grandes cantidades, porque se puede negociar mejores precios. La combinación de factores puede cambiar con la escala de operaciones de la empresa si los directivos pueden aprovechar los factores de menor costo.

Sin embargo, hay un punto a partir del cual es probable que el costo medio de producción comience a aumentar conforme mayor es la producción.

• Al menos a corto plazo, el espacio de la fábrica y la maquinaria pueden hacer que sea más difícil para los trabajadores hacer su trabajo eficazmente.
• Gestionar una empresa mayor puede ser más complejo e ineficiente a medida que aumenta el número de tareas.
• Las ventajas de comprar al por mayor pueden desaparecer una vez que se llega a una determinada cantidad, hay un punto a partir del cual las ofertas de factores clave pueden ser limitadas, lo cual presiona al alza sobre sus costos.

Las curvas a corto y largo plazo

Economías y deseconomías de escala

• Economías de escala: Situación en la que la producción puede duplicarse por menos del doble del costo.

  • La duplicación de la producción no exige una duplicación de los costos.

• Deseconomías de escala: Situación en la que una duplicación de la producción exige una duplicación con creces del costo.

• Las economías de escala suelen medirse por medio de la elasticidad del costo con respecto a la producción \(EC\). \(EC\) es la variación porcentual que experimenta el costo de producción cuando se eleva el nivel de producción un 1 por ciento. \[EC=\frac{\Delta C}{\Delta q}\frac{q}{C}=\frac{CM}{CTMe}\]

Las curvas a corto y largo plazo

La relación entre el costo a corto plazo y el costo a largo plazo

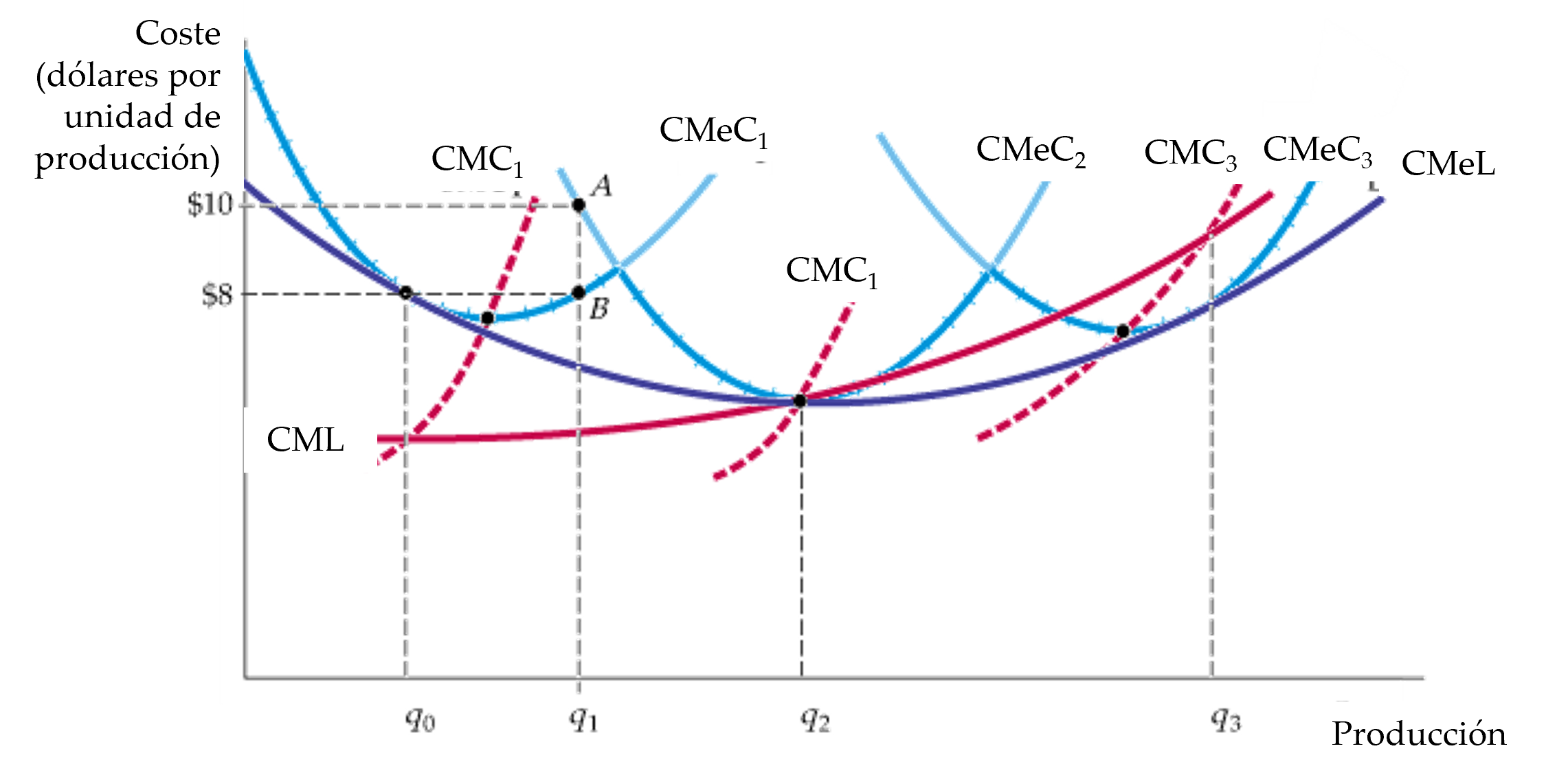
Figura: El costo a largo plazo con economías y deseconomías de escala

La curva de costo medio a largo plazo, CMeL es la envolvente de las curvas de costo medio a corto plazo CMeC1, CMeC2 y CMeC3

Con economías y deseconomías de escala los puntos mínimos de las curvas de costo a medio a corto plazo no se encuentran en la curva de costo medio a largo plazo.

5. La producción con dos productos —Las economías de alcance

Las economías de alcance

• Curva de transformación del producto: Describe las diferentes combinaciones de dos productos que pueden obtenerse con una cantidad fija de factores de producción.

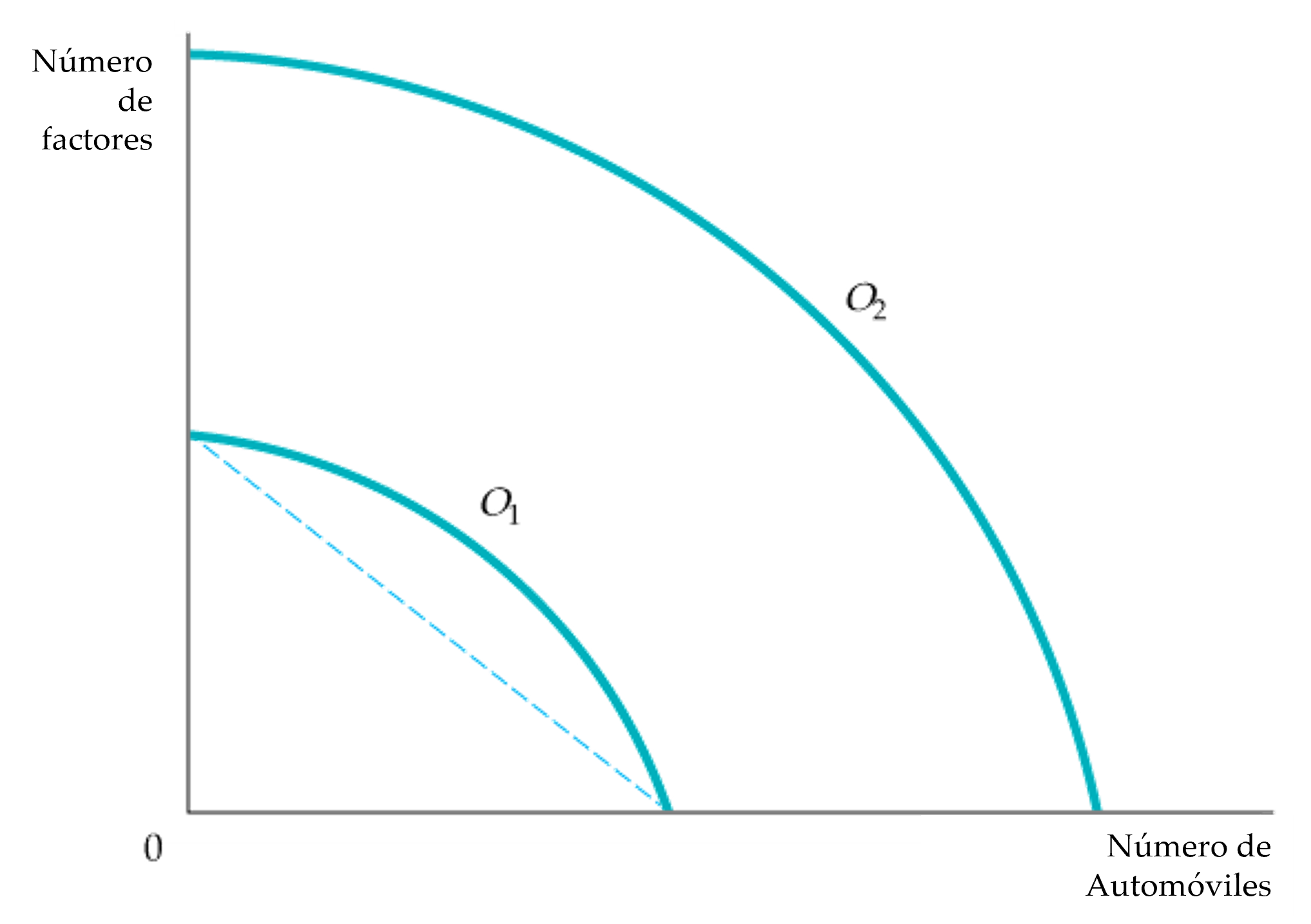
Figura: La curva de transformación del producto

• Las curvas de transformación de los productos \(O_1\) y \(O_2\) están combadas hacia afuera (son cóncavas) porque hay economías de alcance en la producción.
• La curva de transformación del producto muestra las distintas combinaciones de dos productos que pueden producirse con un conjunto dado de factores.

Las economías de alcance

• Economías de alcance: Situación en la que la producción conjunta de una empresa es mayor que la producción que podrían obtener dos empresas cuando cada una produce un único producto.
• Deseconomías de alcance: Situación en que la producción conjunta de una empresa es menor que la que podrían lograr empresas independientes produciendo cada una un único producto.

Las economías de alcance

• Grado de economías de alcance (EA): Porcentaje de ahorro de costos cuando dos o más productos se producen conjuntamente en lugar de individualmente.
• Para medir el grado en que hay economías de alcance, debemos preguntarnos qué porcentaje del costo de producción se ahorra cuando se producen conjuntamente dos (o más) productos en lugar de individualmente.

\[ \text{EA} = \frac{C(Q_1) + C(Q_2) - C(Q_1, Q_2)}{C(Q_1, Q_2)} \]

6. Las variaciones dinámicas de los costos —La curva de aprendizaje

La curva de aprendizaje

• A medida que la dirección y los trabajadores adquieren experiencia en la producción, el costo marginal y el costo medio de producir una determinada cantidad disminuyen por varias razones:
  • Los trabajadores se vuelven más rápidos y eficientes en sus tareas.
  • Los directivos optimizan el proceso de producción.
  • Los ingenieros mejoran el diseño de productos para ahorrar costos sin aumentar los defectos.
  • Los proveedores de materias primas aprenden a elaborar los materiales de manera más eficiente.

La curva de aprendizaje

El costo de producción de una empresa puede disminuir con el tiempo a medida que los directivos y los trabajadores adquieren más experiencia y utilizan más eficazmente la planta y el equipo disponibles.

Figura: La curva de aprendizaje

La curva de aprendizaje muestra el grado en que disminuyen las horas necesarias de trabajo por unidad de producción a medida que aumenta la producción acumulada.

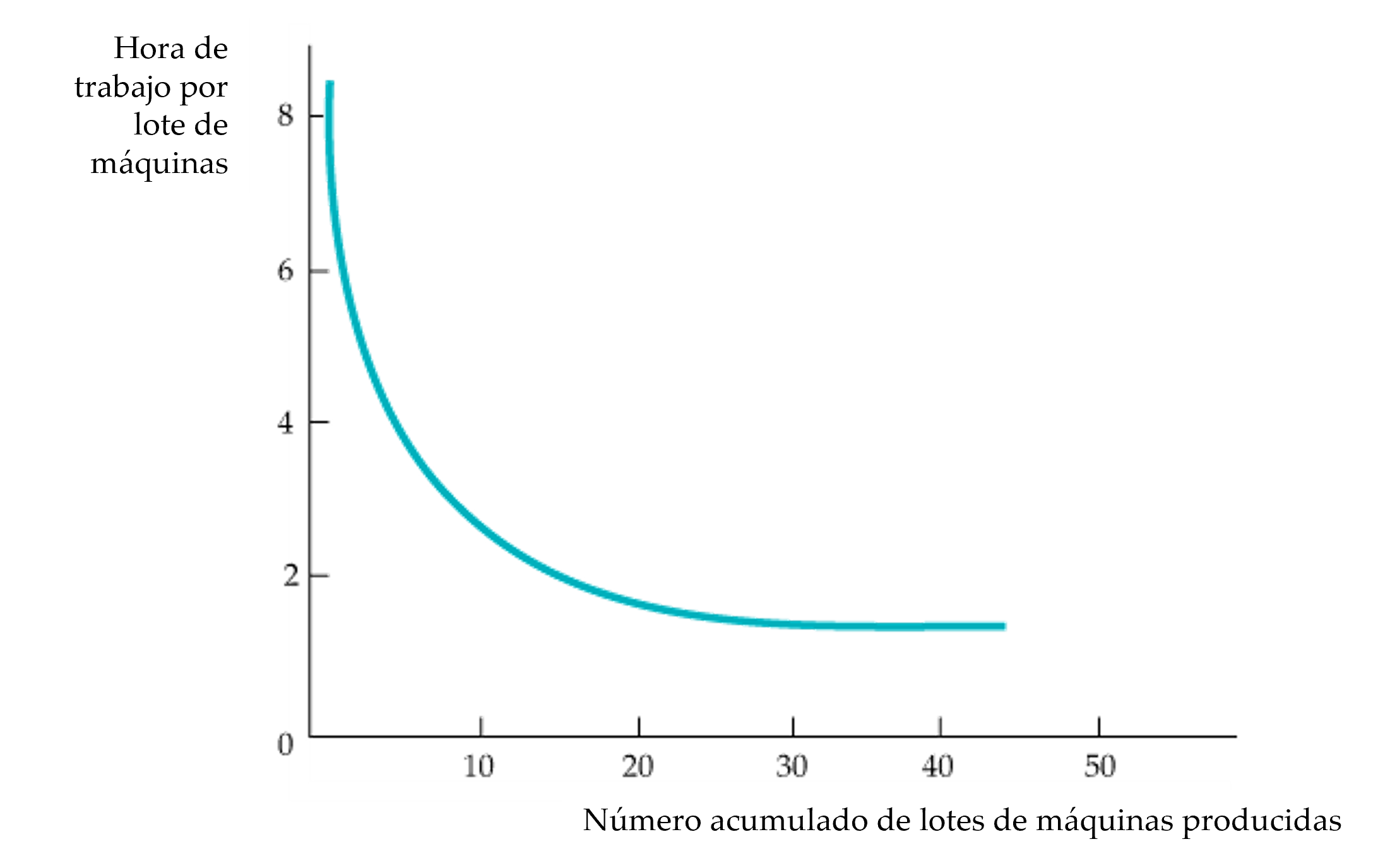
Curva de aprendizaje: Gráfico que relaciona la cantidad de factores que necesita la empresa para producir cada unidad de producción con su producción acumulada.

La curva de aprendizaje

Representación gráfica de la curva de aprendizaje

La curva de aprendizaje se basa en la relación entre la producción acumulada y la cantidad de trabajo necesario por unidad, \(L=A+BN^{-\beta}\).

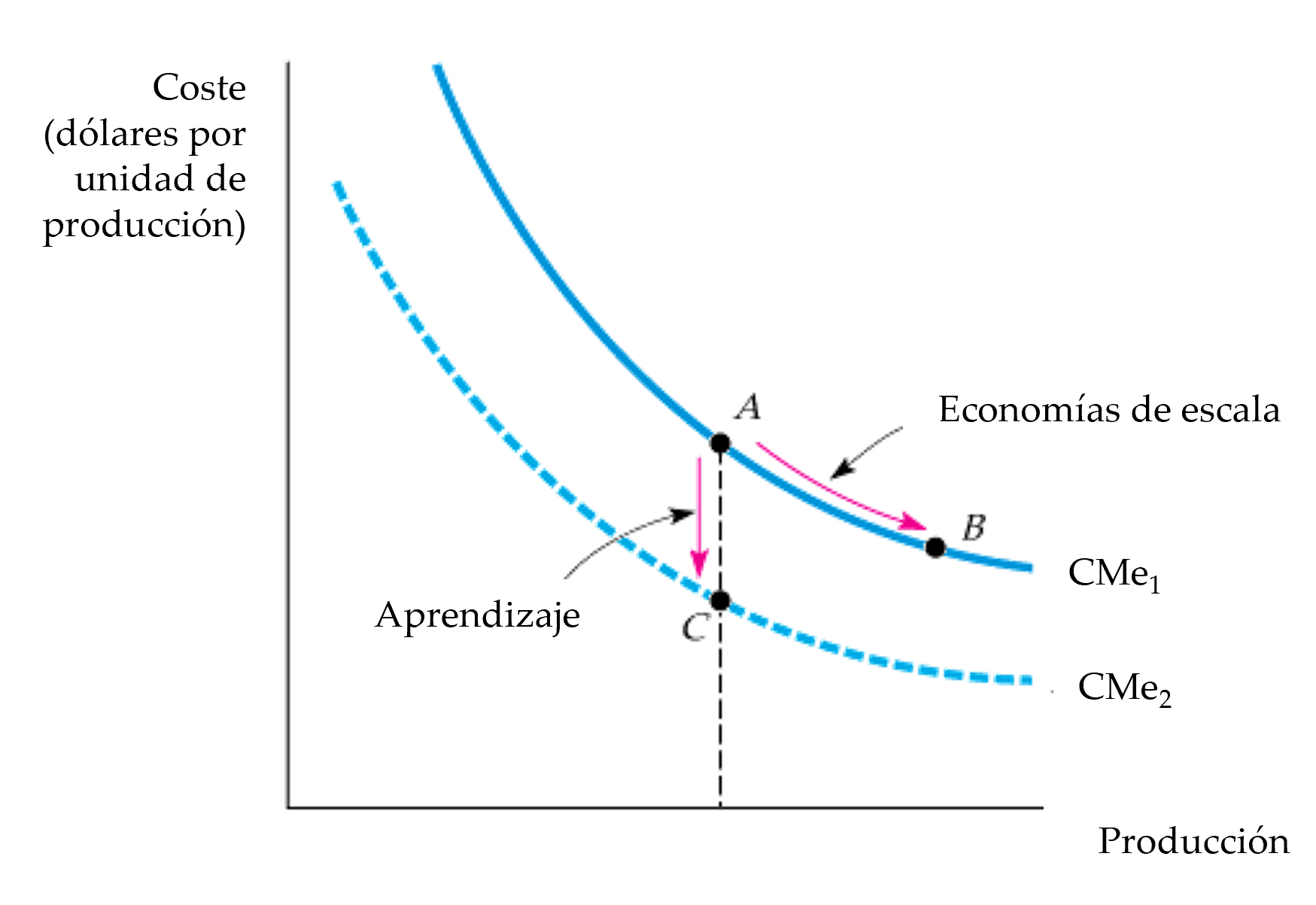
Figura: Aprendizaje frente a economías de escala

• Aprendizaje vs Economías de Escala: El costo medio de producción puede disminuir con el tiempo debido al crecimiento de las ventas o por una curva de aprendizaje.

• El costo medio de producción de una empresa puede disminuir debido a las economías de escala (movimiento de A a B en la curva \(CMe_1\) )

• o debido al aprendizaje (movimiento del punto A en la curva \(CMe_1\) al punto C en la curva \(CMe_2\) ).

La curva de aprendizaje

Aprendizaje versus Economías de Escala

Producción Acumulada (N)	Cantidad de trabajo necesario por unidad para 10 unidades de producción (L)*	Cantidad total de trabajo necesario
10	1.00	10.0
20	0.80	18.0 (10.0 + 8.0)
30	0.70	25.0 (18.0 + 7.0)
40	0.64	31.4 (25.0 + 6.4)
50	0.60	37.4 (31.4 + 6.0)
60	0.56	43.0 (37.4 + 5.6)
70	0.53	48.3 (43.0 + 5.3)
80	0.51	53.4 (48.3 + 5.1)

Nota: Los números de esta columna se calcularon con la ecuación $ (L) = -0.322 (N/10) $, donde \(L\) es la cantidad de trabajo por unidad y \(N\) es la producción acumulada.

7. La estimación y la predicción de costos

La estimación y la predicción de los costos

• Función de costos: Relaciona el costo de producción con el nivel de producción y otras variables controlables por la empresa.
• Curva de costo variable: Puede estimarse empíricamente utilizando datos de las empresas de una industria.

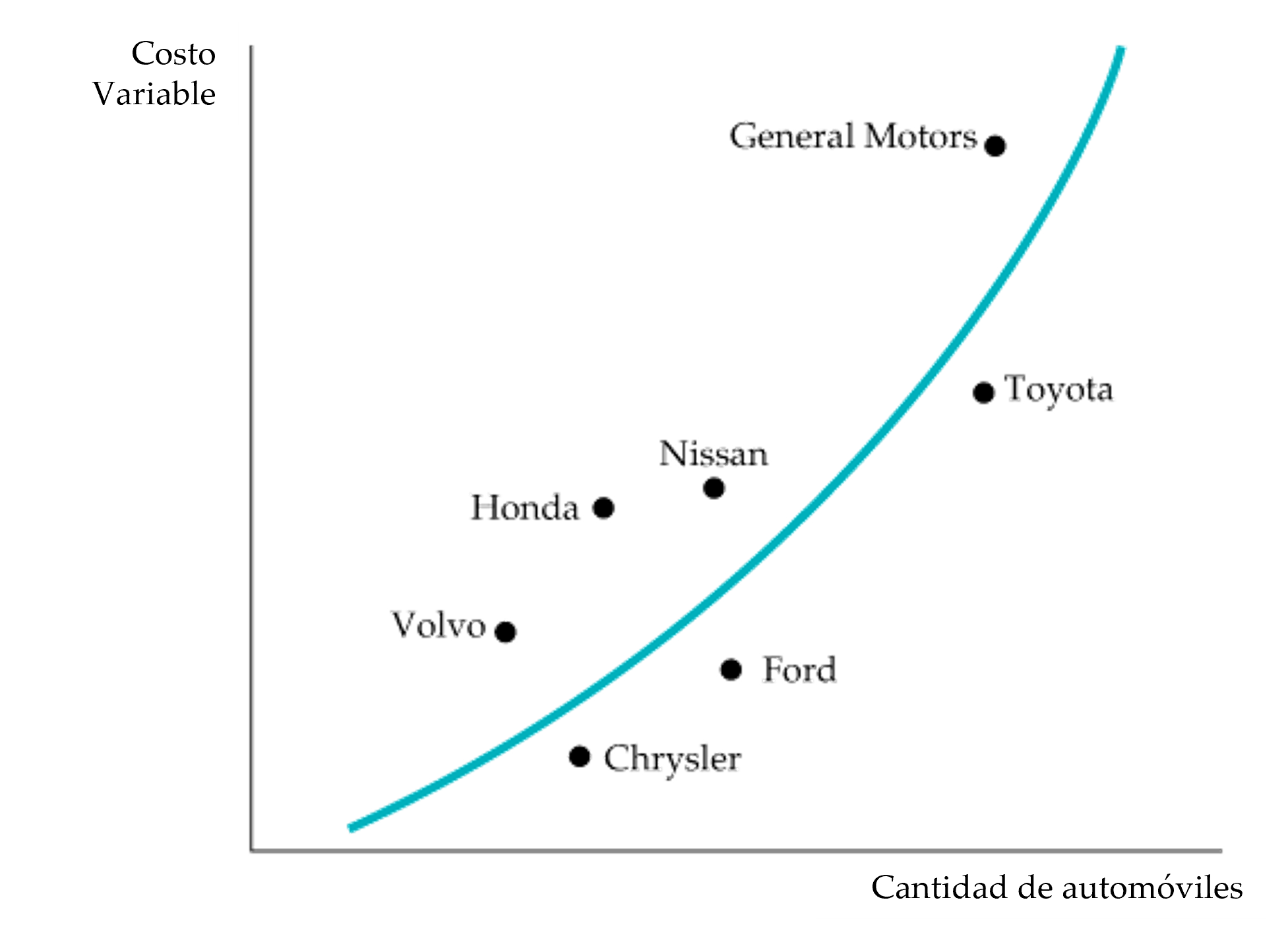
Figura: Curva de costo variable para la industria de automóviles

La curva de costo variable se obtiene determinando estadísticamente la curva que mejor ajusta los puntos que relacionan el nivel de producción de cada empresa y el costo variable de producción.

La estimación y la predicción de los costos

Para producir los costos exactamente, tenemos que averiguar la relación subyancente entre el costo variable y el nivel de producción.

Pero, cuál es la forma de la curva más adecuada y cómo la representamos algebraicamente? He aquí una función de costos que podríamos elegir: \[CV=\beta q\]

Si queremos que la curva de costo medio tenga forma de U y que el costo marginal no sea constante, debemos utilizar una función de costos más compleja. Una posibilidad es la función de costos cuadrática, que relaciona el costo variable con el nivel de producción y con el nivel de producción al cuadrado: \[CV=\beta q+\gamma q^2\]

Si la curva de costo marginal no es lineal, podemos utilizer una función de costos cúbica: \[CV=\beta q+\gamma q^2+\phi q^3\]

La estimación y la predicción de los costos

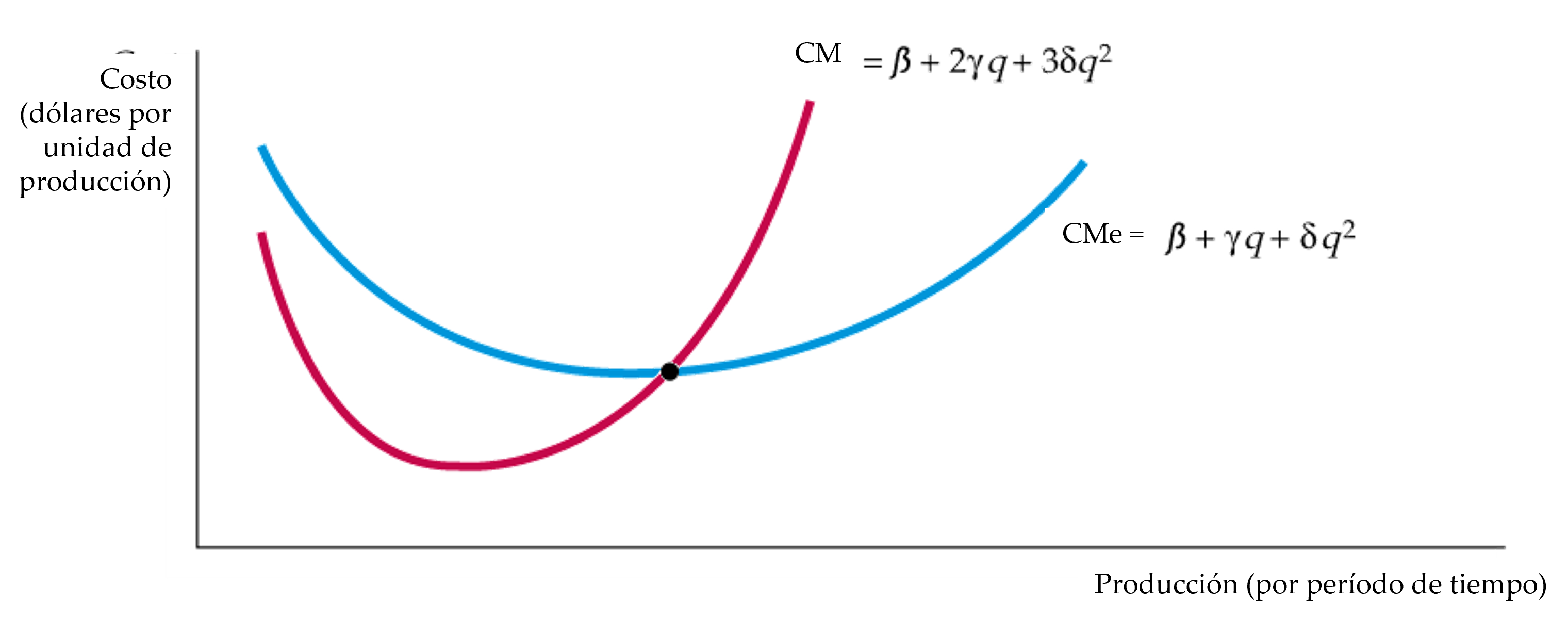
La función de costos cúbica

Si la curva de costo medio tiene forma de U y el costo marginal no es constante, se debe utilizar una función de costos más compleja. La función de costos cúbica implica que las curvas de costo medio y marginal tienen forma de U.

La estimación y la predicción de los costos

Las funciones de costos y la medición de las economías de escala

• Índice de economías de escala (IEE): Un índice que indica si hay o no economías de escala.

\[ \text{IEE} = 1 - E_c \]

• El IEE se define como \(IEE = 1 - E_c\), donde \(E_c\) es la elasticidad del costo con respecto a la producción.

Cierre

¿Preguntas?