Fijación de Precios con Poder de Mercado
Microeconomía
Contenido
Captura del Excedente del Consumidor
Discriminación de Precios (1º, 2º y 3º grado)
Discriminación Intertemporal y Precios Pico
Tarifa de Dos Partes
Agrupamiento de Productos
Publicidad
Captura del Excedente del Consumidor
- Estrategia de precios: método para fijar precios según el entorno competitivo.
- Discriminación de precios: cobrar precios distintos a consumidores distintos por bienes/servicios similares.
Si una empresa puede cobrar solo un precio para todos sus clientes, ese precio será P* y la cantidad producida será Q* .
Idealmente, la empresa desea cobrar un precio más alto a los consumidores dispuestos a pagar más de P* , capturando así parte del excedente del consumidor bajo la región A de la curva de demanda. La empresa también desea vender a consumidores dispuestos a pagar precios más bajos que P*, pero solo si hacerlo no implica bajar el precio a otros consumidores.
Ejemplos: tarifas aérea “flex vs. económica”; planes youtube regular/estudiante; planes gimnasio “Basic/Pro” o por horarios.
Discriminación de Precios de Primer Grado
- Precio de reserva: Precio máximo que un cliente está dispuesto a pagar por un bien.
- Discriminación de precios de primer grado (o perfecta): Práctica de cobrar a cada ‘unidad’ (ej. cliente) su precio de reserva.
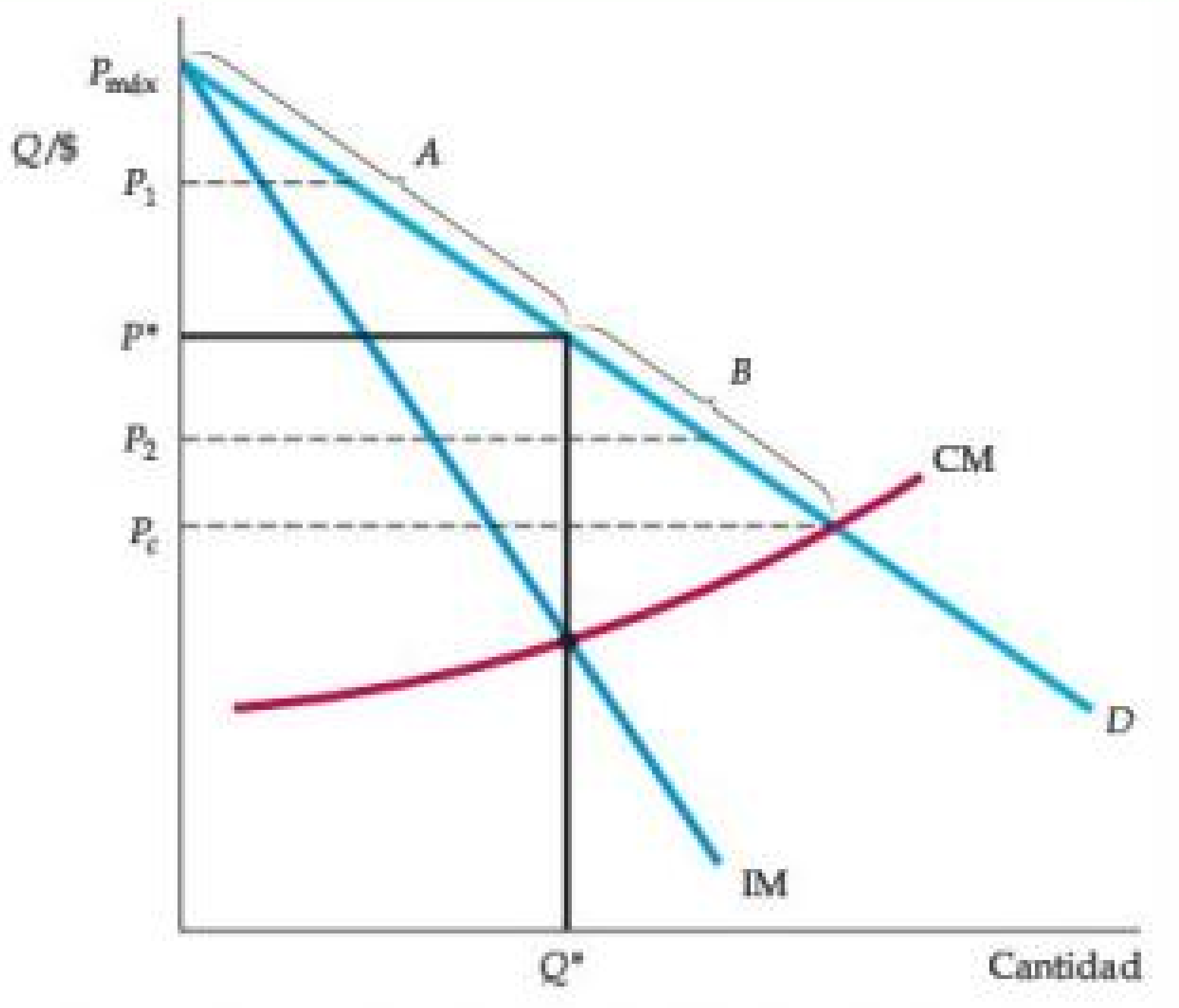
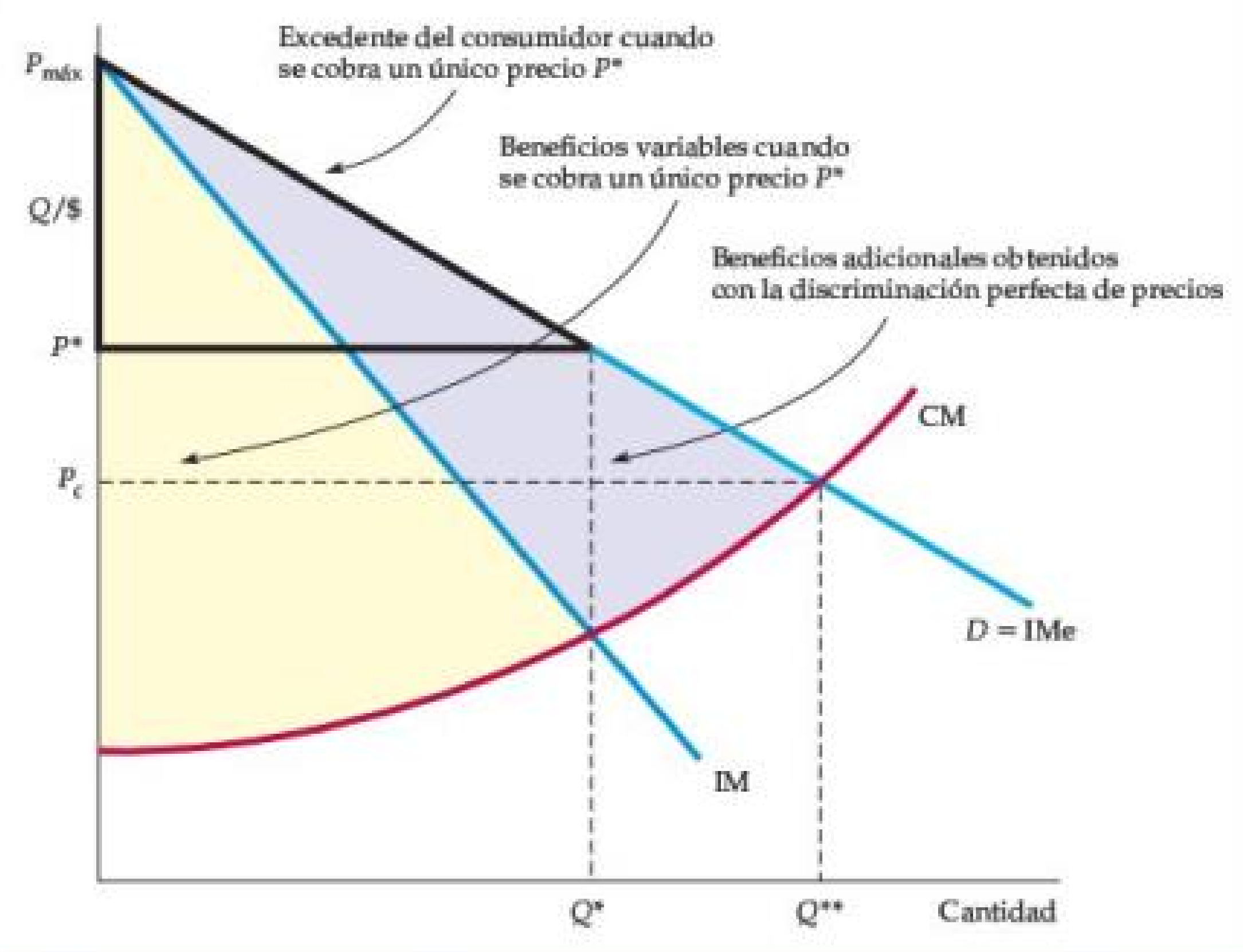
Figura: Ganancia Adicional de la Discriminación Perfecta de Precios de Primer Grado.
- Debido a que la empresa cobra a cada consumidor su precio de reserva, es rentable expandir la producción a Q** .
- Cuando solo se cobra un precio P* , la ganancia variable de la empresa es el área entre las curvas de ingreso marginal y costo marginal.
- Con la discriminación perfecta de precios, esta ganancia se expande al área entre la curva de demanda y la curva de costo marginal.
Discriminación de Precios (cont.)
1.er grado en la práctica.
Normalmente no se conoce el precio de reserva exacto; se aproximan menús de precios.
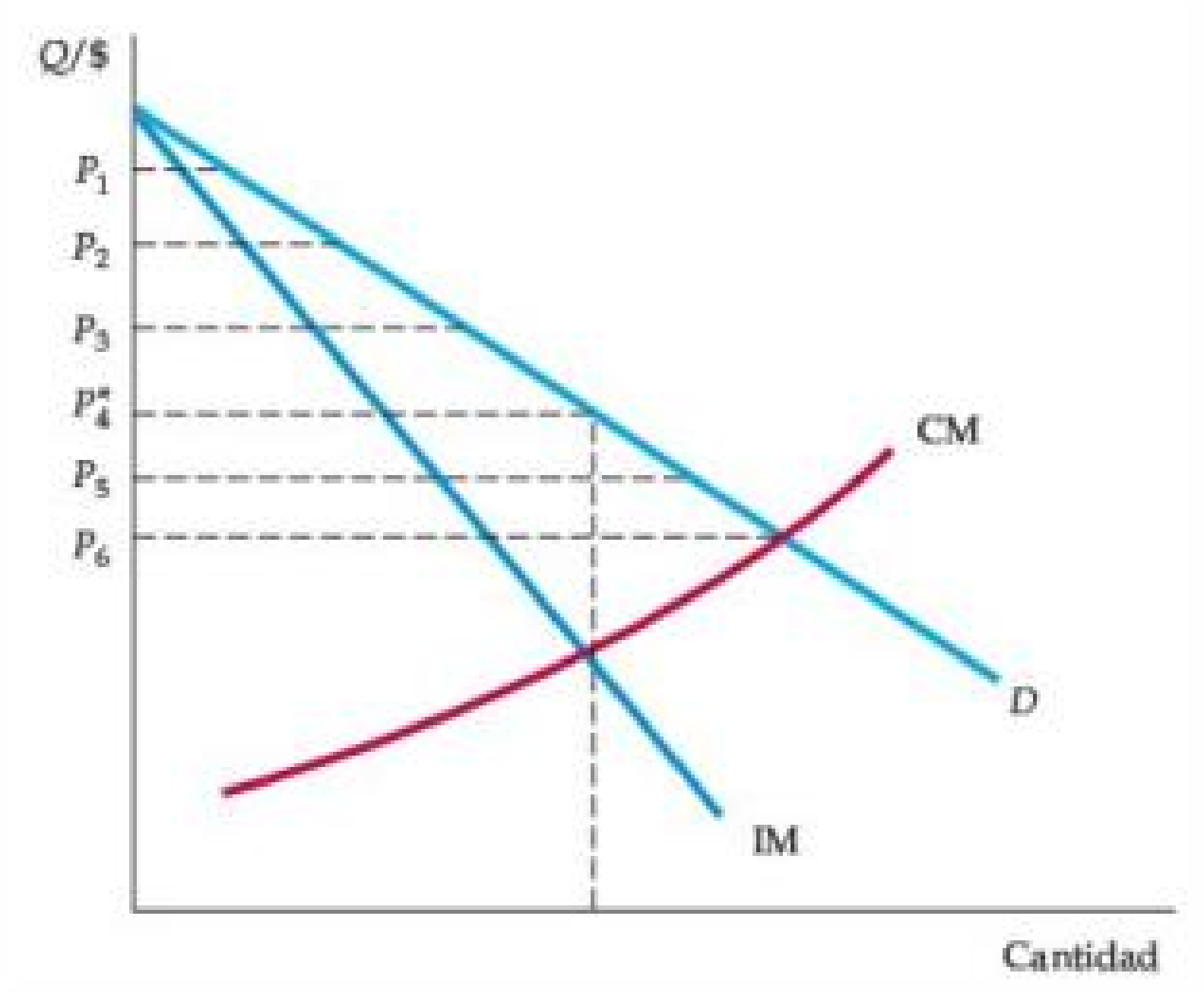
Figura: Discriminación de Precios de Primer Grado
Ejemplos: regateo (autos usados), subastas, “versioning” de software (ediciones con funciones).
- Las empresas generalmente no conocen el precio de reserva de cada consumidor, pero a veces se pueden identificar aproximadamente los precios de reserva.
- Aquí se cobran seis precios diferentes. La empresa obtiene mayores ganancias, pero algunos consumidores también pueden beneficiarse.
- Con un precio único P4 hay menos consumidores.
- Los consumidores que ahora pagan P5 o P6 disfrutan de un excedente.
Discriminación Perfecta de Precios
Ejemplo
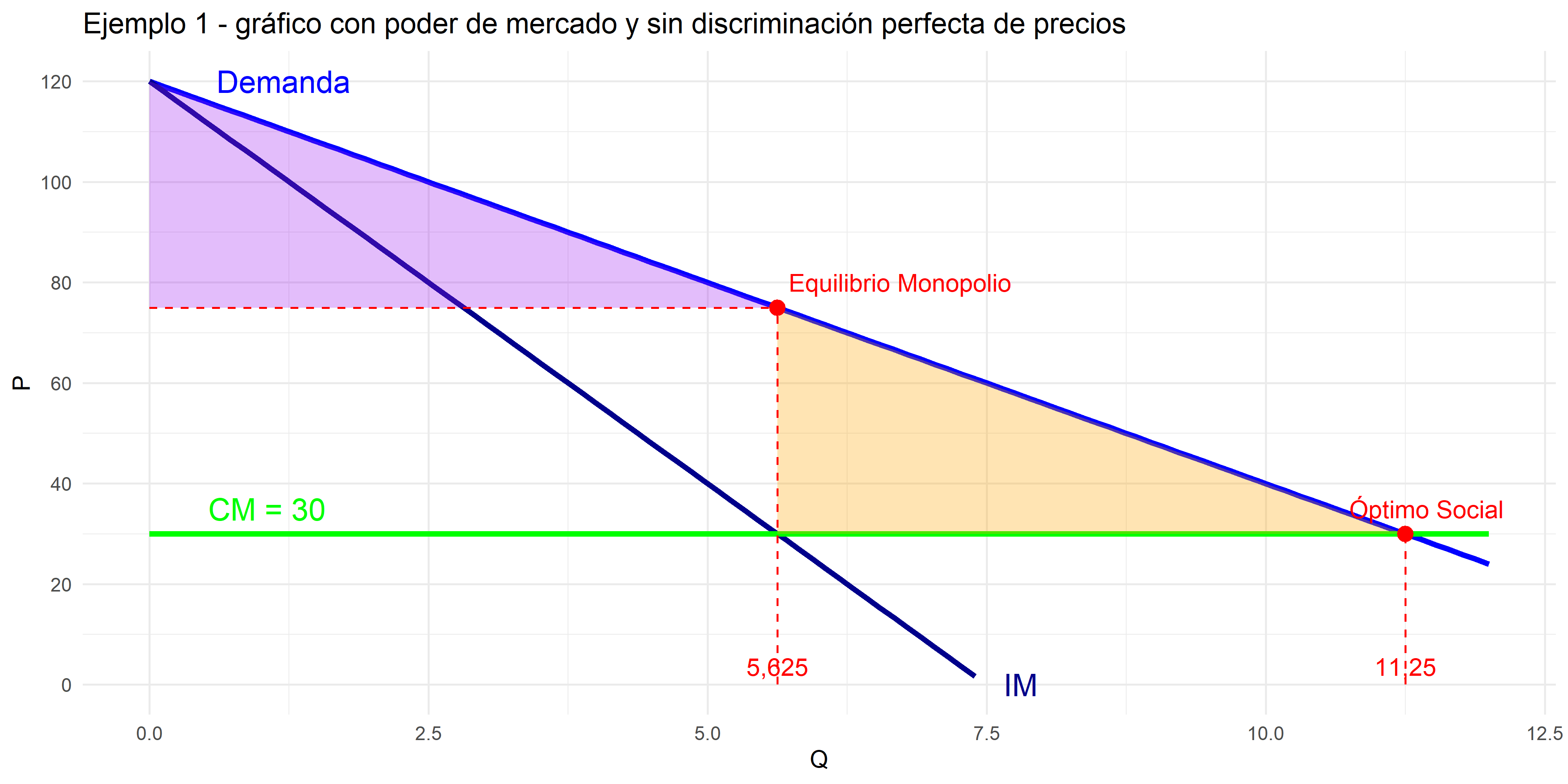
Una empresa con poder de mercado enfrenta una curva (inversa) de demanda dada por P=120 – 8\cdot Q . Además, la empresa enfrenta costos totales de C(Q)=20+30\cdot Q (o \Rightarrow CM=30).
- Si la empresa no puede discriminar precios: ¿Cuál es la cantidad que produce la empresa y cuál es el precio que maximiza beneficios? Además, determinar el excedente del consumidor, del productor, y la pérdida económica o de bienestar.
- Si la empresa pudiera practicar discriminación perfecta de precios: ¿Cuál sería el último precio que cobraría? Determinar el excedente del consumidor, el excedente del productor y la pérdida económica o de bienestar.
Discriminación Perfecta de Precios
Ejemplo - respuesta (sin discriminación de precios)
- El ingreso total es I = P \cdot Q = (120 - 8Q)Q = 120Q - 8Q^2.
Así, el ingreso marginal es IM = \frac{d(I)}{dQ} = 120 - 16Q. - Al igualar IM con CM, se encuentra la cantidad que maximiza beneficio: 120 - 16Q = 30.
Es decir, Q = 5,625. Y el precio asociado es P = 120 - 8 \cdot 5,625 =75. - El excedente del consumidor es el área del triángulo entre la curva de demanda y el precio de mercado:
EC = \frac{1}{2} \cdot (120 - 75) \cdot 5,625 = 126,56 - El excedente del productor es: EP = (75 - 30) \cdot 5,625 = 253,12
- La pérdida económica o de bienestar es el área del triángulo entre el punto donde la cantidad socialmente óptima (P = CM) y la cantidad producida por el monopolio.
- Cantidad: P = 120 - 8Q= CM=30, es decir, Q = 11,25.
- Pérdida de bienestar es: PE = \frac{1}{2} \cdot (11,25 - 5,625) \cdot (75 - 30) = 126,56
Discriminación Perfecta de Precios
Discriminación Perfecta de Precios
Ejemplo - respuesta (con discriminación de precios)
- La empresa cobra un precio diferente a cada unidad vendida, igual al valor de la demanda. Así, el último precio que cobraría corresponde al precio para la última unidad vendida. Si la empresa produce hasta el punto donde P = CM, se tiene que P = CM = 30.
- Excedente del consumidor (EC): Con discriminación perfecta de precios, el excedente del consumidor es 0, ya que la empresa captura todo el valor de la demanda.
- Excedente del productor (EP): Es el área bajo la curva de demanda y por encima del costo marginal EP = \frac{(120-30)11,25}{2}=506,25
- Pérdida económica (PE): Con discriminación perfecta de precios, no hay pérdida económica o de bienestar, ya que la empresa produce la cantidad socialmente óptima y captura todo el excedente del consumidor.
Por lo tanto, el excedente del productor es 506,25, el excedente del consumidor es 0 y la pérdida económica es 0.
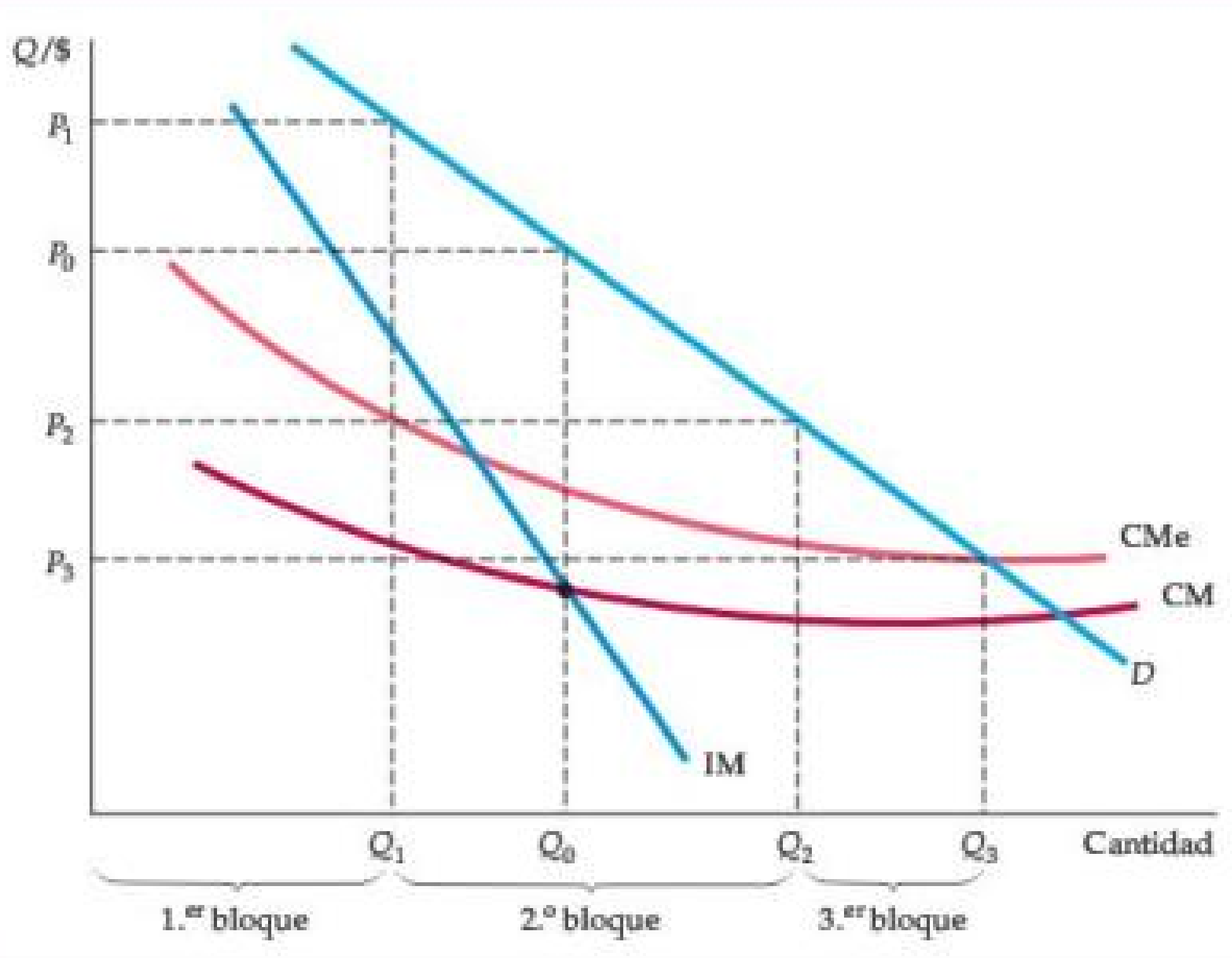
Discriminación de Precios de Segundo Grado
- discriminación de precios de segundo grado: Práctica de cobrar diferentes precios por unidad para diferentes cantidades del mismo bien o servicio. El consumidor se autoselecciona.
Figura: Discriminación de Precios de Segundo Grado
- Se cobran diferentes precios por diferentes cantidades o “bloques” del mismo bien. Aquí hay tres bloques con precios correspondientes P1, P2 y P3.
- También hay economías de escala y los costos promedio y marginales están disminuyendo. La discriminación de precios de segundo grado puede entonces beneficiar a los consumidores al expandir la producción y reducir los costos.
Ejemplos: tarifas de agua/luz por tramos; copisterías con descuento por volumen; planes de datos móviles.
Discriminación de Precios de Segundo Grado
Ejemplo
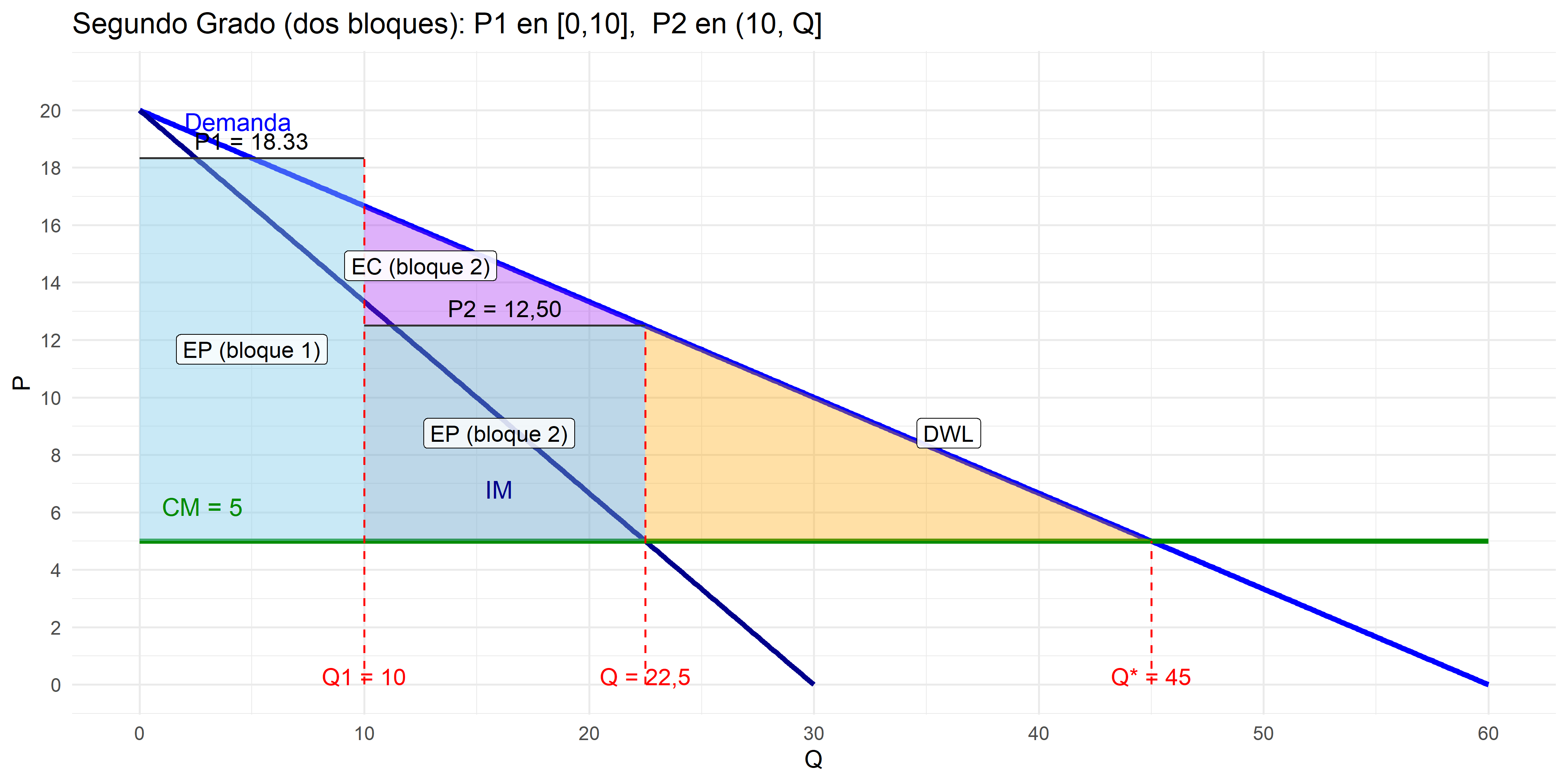
Monopolista con C(Q)=100+5Q y demanda inversa p(Q)=20-\tfrac{1}{3}Q ofrece dos bloques:
- Bloque 1: primeras 10 unidades a precio P_1.
- Bloque 2: unidades por sobre 10 a precio P_2.
- Elegir P_1 y P_2 para maximizar beneficios (precios lineales por bloque).
- Calcular Q, EC, EP (sobre CM=5) y la pérdida de bienestar.
Discriminación de Precios de Segundo Grado
Ejemplo — Respuesta
- Para P_2: IM=CM \Rightarrow IM=120-\tfrac{2}{3}Q=CM=5 \Rightarrow Q=22{,}5 \Rightarrow \boxed{P_2=12{,}5}.
- Para encontrar P_1 hay que considerar que se busca extraer el valor inframarginal o valor adicional de las primeras unidades (en el intervalo [0,10]). La empresa puede capturar esa diferencia cobrando un precio promedio mayor en el primer bloque. Como la demanda es lineal, el precio promedio es:
- Para Q=0, se tiene que p(0)=20. Para Q=10, p(10)=20-\tfrac{1}{3}\cdot 10=\mathbf{16{,}67}.
- El precio medio (en un tramo lineal es el promedio de extremos), que deja EC_1=0, es: \boxed{P_1=\frac{20+16{,}67}{2}=\mathbf{18{,}33}}
- Alternativamente, este resultado se puede obtener de forma más general: P_1=\tfrac{1}{10}\int_0^{10}\!\left(20-\tfrac{1}{3}q\right)dq=18{,}33
- Para Q=0, se tiene que p(0)=20. Para Q=10, p(10)=20-\tfrac{1}{3}\cdot 10=\mathbf{16{,}67}.
Discriminación de Precios de Segundo Grado — Gráfico (dos bloques)
Discriminación de Precios de Segundo Grado
Ejemplo — Respuesta (cont.): EC, EP y pérdida de bienestar
- Excedente del consumidor (EC):
- En el bloque 1, con Q\in[0,10], tenemos EC_1=0 (por construcción).
- En el bloque 2, con Q\in[10\,,\,22.5], tenemos a Q=10, brecha =16{,}67-12{,}5=\mathbf{4{,}17}; a Q=22{,}5, brecha =0.
- Área = triángulo: base =12{,}5, altura =4{,}17:
- \Rightarrow\; EC_2=\tfrac{1}{2}\cdot 12{,}5\cdot 4{,}17=\mathbf{26{,}04}.
- En el bloque 1, con Q\in[0,10], tenemos EC_1=0 (por construcción).
- Excedente del productor (EP) sobre CM=5.
- Bloque 1: rectángulo (P_1-5)\cdot 10=(18{,}33-5)\cdot 10=\mathbf{133{,}3}.
- Bloque 2: rectángulo (P_2-5)\cdot 12{,}5=(12{,}5-5)\cdot 12{,}5=\mathbf{93{,}75}.
- \Rightarrow\; \boxed{EP=\mathbf{227{,}05}\ (\approx 227{,}08)}.
- Bloque 1: rectángulo (P_1-5)\cdot 10=(18{,}33-5)\cdot 10=\mathbf{133{,}3}.
Discriminación de Precios de Segundo Grado
Otro Ejemplo
Ejemplo en donde se ilustra que el precio marginal depende de la cantidad (precio por unidad por bloque)
Un monopolista con costos totales C(Q) = 100 + 5Q enfrenta una curva de demanda q_1 = 60 - 3p_1 y puede diferenciar dos tipos de bloques de precios: los que compran hasta 10 unidades (bloque 1) y los que compran más de 10 unidades (bloque 2).
- Determine los precios P_1 y P_2 que la empresa debe cobrar para maximizar sus beneficios.
- Calcule el excedente del consumidor, el excedente del productor y la pérdida económica o de bienestar bajo esta estrategia de discriminación de precios.
Discriminación de Precios de Segundo Grado
Otro Ejemplo — respuesta
- Determinación de precios y cantidades en cada bloque.
- bloque 1 (hasta 10 unidades): La demanda inversa es p_1 = 20 - \frac{1}{3}q_1 y por ende P_1 = 20 - \frac{1}{3} \cdot 10 = 20 - 3,33 = 16,67 .
- bloque 2 (sobre 10 unidades): La empresa debe establecer el precio de manera que maximice sus beneficios teniendo en cuenta los costos marginales constantes de CM = 5 . Es decir, al resolver IM=\frac{d((20Q - \frac{1}{3}Q^2))}{dQ} = 20 - \frac{2}{3}Q =CM=5 se obtiene Q = 22,5. Así, las unidades adicionales del segundo bloque, serán Q_2 = 22,5 - 10 = 12,5. Además, al sustituir Q = 22,5 en la curva de demanda se obtiene P_2 = 20 - \frac{1}{3} \cdot 22,5 = 12,5.
Discriminación de Precios de Segundo Grado
Otro Ejemplo — respuesta (cont.)
- Excedente del consumidor, del productor y la pérdida económica:
Excedente del consumidor (EC): área del triángulo entre la curva de demanda y el precio pagado por los consumidores.
- Primer bloque: EC_1 = \frac{1}{2} \cdot (20 - 16.67) \cdot 10 = 16,65
- Segundo bloque: EC_2 = \frac{1}{2} \cdot (16.67 - 12.5) \cdot 12.5 = 26,06
- Excedente total del consumidor es: 16,65 + 26,06 = 42,71
Excedente del productor (EP): área del rectángulo entre el precio pagado por los consumidores y el costo marginal.
- Primer bloque: EP_1 = (16,67 - 5) \cdot 10 = 116,7
- Segundo bloque: EP_2 = (12,5 - 5) \cdot 12,5 = 93,75
- Excedente total del productor es: 116,7 + 93,75 = 210,45
Pérdida económica (PE): área del triángulo entre la cantidad socialmente óptima (P = CM) y la cantidad producida por el monopolio.
- Cantidad socialmente óptima: 20 - \frac{1}{3}Q = 5 , es decir, Q = 45.
- Pérdida de bienestar: PE = \frac{1}{2} \cdot (45 - 22,5) \cdot (p(22{,}5)-5) =\tfrac12(45-22{,}5)\cdot 7{,}5=\mathbf{84{,}38}.
Discriminación de Precios de Tercer Grado
- Discriminación de precios de tercer grado: la empresa separa a los consumidores en dos o más grupos con curvas de demanda distintas (segmentación observable, sin reventa) y cobra precios diferentes a cada grupo.
Intuición de las condiciones para aplicarla:
- La firma puede segmentar. Por ejemplo, estudiante vs. general; residente vs. turista; país A vs. país B.
- No hay arbitraje/reventa entre grupos.
- El costo marginal depende de la producción total Q_T.
Por ejemplo, las entradas a cine o museos poseen descuento por perfiles: las de estudiantes tienen precio más bajo (donde la demanda es más elástica).
Discriminación de Precios de Tercer Grado
Crear Grupos de Consumidores
- Sabemos que, independientemente de cuánto se produzca, la producción total debe dividirse entre los grupos de clientes: Q_T=Q_1+Q_2
- La producción total, debe ser tal que el ingreso marginal para cada grupo de consumidores sea igual al costo marginal de producción: \frac{\partial\pi}{\partial Q_i}=\frac{\partial(P_1Q_1+P_2Q_2-C(Q_T))}{\partial Q_i} \;=\; IM_i - CM(Q_T)\;=\;0 \quad\Rightarrow\quad IM_1 \;=\; IM_2 \;=\; CM(Q_T).
Es decir, producir y vender en cada grupo hasta que su ingreso marginal sea igual al costo marginal común (evaluado en Q_T). La producción total se reparte entre mercados de forma que igualen sus ingresos marginales.
Discriminación de Precios de Tercer Grado
Determinación de precios relativos — Regla con elasticidades
Con demanda (inversa) por grupo y elasticidad-precio \varepsilon_i(<0): IM_i \;=\; P_i\!\left(1+\frac{1}{\varepsilon_i}\right)
Por tanto, en el óptimo: \frac{P_1}{P_2}=\frac{(1+1/\xi_2)}{(1+1/\xi_1)}
Es decir, el grupo con demanda más elástica (mayor |\varepsilon|) recibe precio menor.
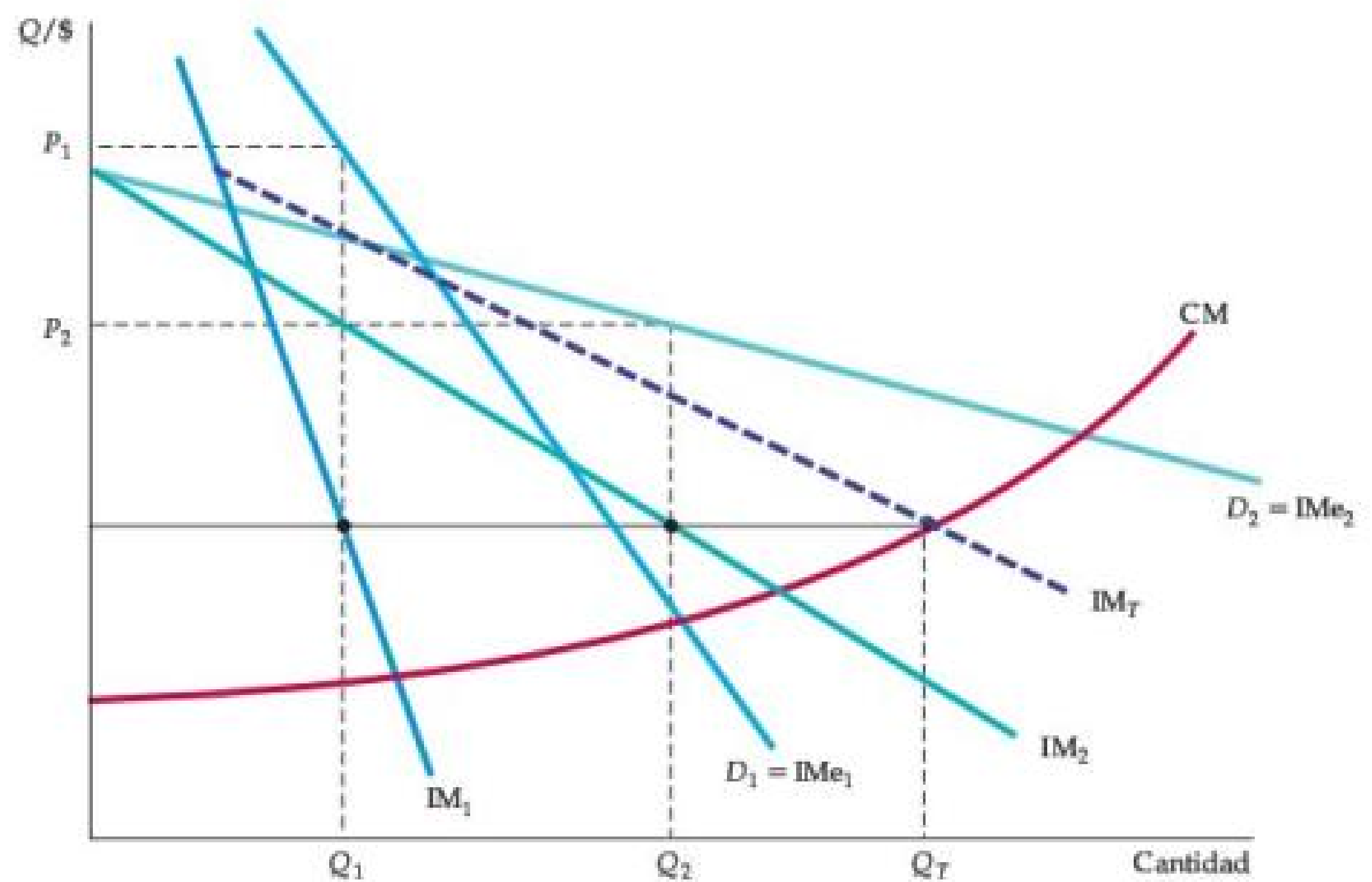
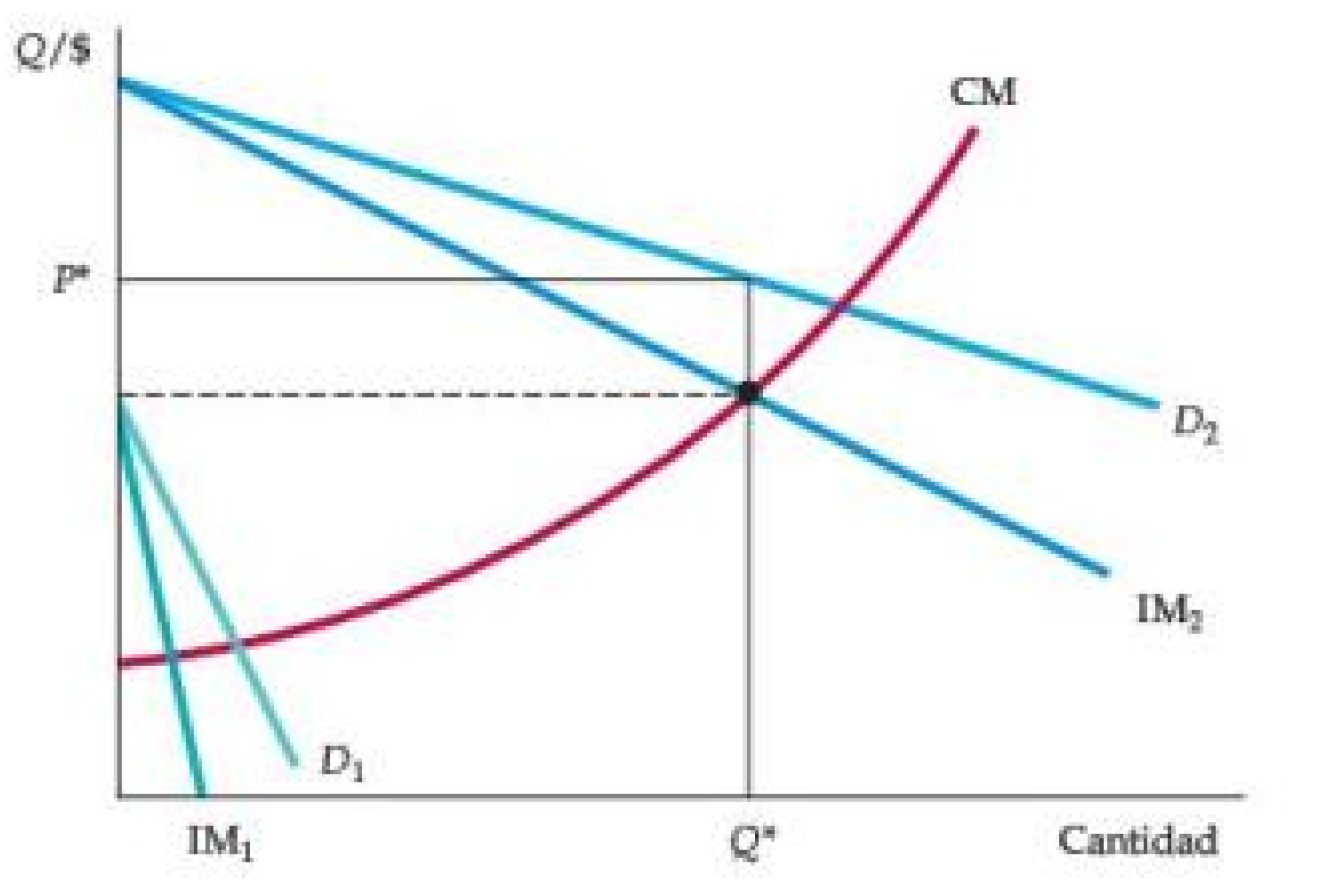
Figura: Discriminación de Precios de Tercer Grado
- Los consumidores se dividen en dos grupos con curvas de demanda separadas para cada grupo. Los precios y cantidades óptimos son tales que el ingreso marginal de cada grupo es el mismo y es igual al costo marginal.
- Aquí, el grupo 1 con la curva de demanda D1 se cobra P1 y el grupo 2 con la curva de demanda más elástica D2 se cobra el precio más bajo P2.
- El costo marginal depende de la cantidad total producida QT. Tenga en cuenta que Q1 y Q2 se eligen de manera que IM1 = IM2 = MC.
- Resulta P_1>P_2 si D_1 es menos elástica que D_2.
Discriminación de Precios de Tercer Grado
Determinación de Precios Relativos (cont.)
Con CM creciente, puede no ser rentable servir al mercado con muy baja disposición a pagar (o muy pequeña) porque el precio requerido sería inferior al CM asociado a Q_T. En ese caso, la firma vende solo al grupo con mayor disposición a pagar y satisface IM_2=CM(Q_T).
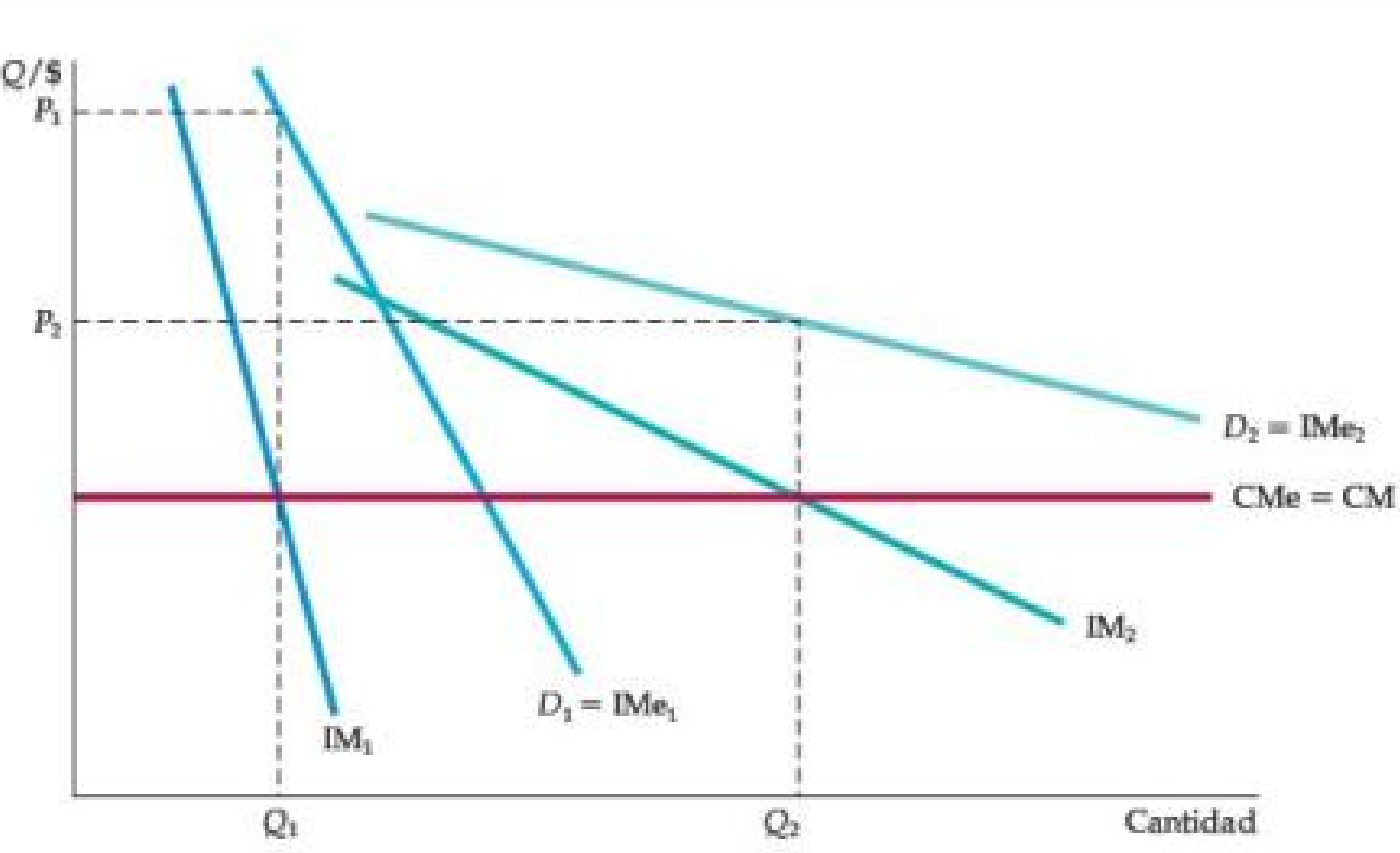
Figura: No Ventas al Mercado Menor
- La figura ilustra el caso en que incluso si la discriminación de precios de tercer grado es factible, puede no ser rentable vender a ambos grupos de consumidores si el costo marginal está aumentando.
- Aquí, el primer grupo de consumidores con demanda D1 no está dispuesto a pagar mucho por el producto.
- No es rentable venderles porque el precio tendría que ser demasiado bajo para compensar el aumento resultante en el costo marginal.
Discriminación de Precios de Tercer Grado
Ejemplo
Un monopolista con costos totales C(Q)=300+5Q puede diferenciar dos tipos de clientes, cuyas curvas de demanda son: q_1=50-4p_1,\qquad q_2=30-3p_2.
- Si puede hacer discriminación de precios de tercer grado, determine precios y cantidades en cada mercado.
- Con esos resultados, calcule la elasticidad en cada mercado y concluya dónde será mayor el precio (mercado más o menos elástico).
- Si el regulador obliga a precio único para todos, encuentre el precio y la cantidad óptimos.
Discriminación de Precios de Tercer Grado
Ejemplo - respuesta (1): precios y cantidades por mercado
A partir de la información entregada, el Costo Marginal (CM) es CM = \frac{dC(Q)}{dQ} = 5.
- Mercado 1: La demanda inversa es p_1 = 12,5 - 0,25q_1 y por ende el ingreso marginal (IM) es IM_1 = \frac{d(p_1*q_1)}{dq_1} = 12,5 - 0,5q_1. Así, la cantidad que maximiza beneficios (IM=CM) se obtiene de 12,5 - 0,5q_1 = 5, es decir, q_1 = 15. Al reemplazar en la curva de demanda inversa, p_1 = 12,5 - 0,25 \cdot 15 = 12,5 - 3,75 = 8,75.
- Mercado 2: La demanda inversa es p_2 = 10 - \frac{1}{3}q_2 y por ende IM_2 = 10 - \frac{2}{3}q_2. Así, la cantidad que maximiza beneficios se obtiene de resolver 10-\frac{2}{3}q_2=5 , es decir, q_2 = 7,5. Finalmente, al reemplazar se obtiene p_2 = 7,5.
Discriminación de Precios de Tercer Grado
Ejemplo - respuesta (2): elasticidades y precios relativos
- Determinación de la elasticidad (\varepsilon=\dfrac{dq}{dp}\cdot\dfrac{p}{q}) en cada mercado y análisis de precios:
- Mercado 1: La elasticidad es \xi_1=\frac{dq_1}{dp_1}\frac{p_1}{q_1} = -4 \cdot \frac{8.75}{15} = -2.33 .
- Mercado 2: La elasticidad es \xi_2=\frac{dq_2}{dp_2}\frac{p_2}{q_2} = -3 \cdot \frac{7.5}{7.5} = -3 .
Conclusión: La elasticidad es mayor (en valor absoluto) en el mercado 2, |\varepsilon_2|>|\varepsilon_1|. Por lo tanto, el mayor precio se encuentra en el mercado menos elástico (mercado 1). Alternativamente, como el mercado 2 es más elástico, p_2<p_1.
Chequeo con la regla: IM=CM \Rightarrow P=\dfrac{CM\,|\varepsilon|}{|\varepsilon|-1} da P_1=5\cdot\frac{2{,}33}{1{,}33}\approx8{,}75 y P_2=5\cdot\frac{3}{2}=7{,}5.
Discriminación de Precios de Tercer Grado
Ejemplo - respuesta (3): precio único regulado
Demanda agregada con precio único p:
Q=q_1+q_2=(50-4p)+(30-3p)=80-7p
\Rightarrow\; p(Q)=\tfrac{80}{7}-\tfrac{1}{7}Q,\quad IM(Q)=\tfrac{80}{7}-\tfrac{2}{7}Q.
IM=CM \Rightarrow \tfrac{80}{7}-\tfrac{2}{7}Q=5 \Rightarrow Q=\mathbf{22{,}5},
P=p(Q)=\frac{80-22{,}5}{7}=\mathbf{8{,}21}.
En este ejemplo, Q total coincide con el de la discriminación: 15+7{,}5=22{,}5, aunque la asignación por mercado cambia.
Discriminación Intertemporal de Precios
Discriminación intertemporal de precios: separar consumidores a lo largo del tiempo cobrando primero un precio alto (P_1) y luego un precio menor (P_2); segmenta por costo de esperar / urgencia (alta vs. baja).
- Ejemplo: lanzamiento de smartphones/videojuegos (precio alto al inicio y rebaja meses después).
Figura: Discriminación Intertemporal de Precios
- Los consumidores se dividen en grupos al cambiar el precio con el tiempo.
- En t_1, P_1 vende a quienes valoran la novedad/inmediatez (no esperan); en t_2, P_2<P_1 capta al resto (más pacientes).
- Luego, el precio se reduce para atraer al mercado masivo.
- Condiciones clave: (i) baja reventa entre períodos, (ii) posibilidad de compromiso en precios futuros (evita el problema del monopolista de bienes durables), (iii) el producto no debe depreciarse “demasiado” entre t_1 y t_2.
Fijación de Precios por Peaks de Demanda
Precios por Peaks de Demanda: En períodos altos o pico la capacidad es vinculante, es decir, el CM efectivo es más alto; conviene fijar P_{\text{peak}}>P_{\text{valle}}.
- Ejemplo: Las tarifas eléctricas por horario o los peajes urbanos con tarifa punta/valle.
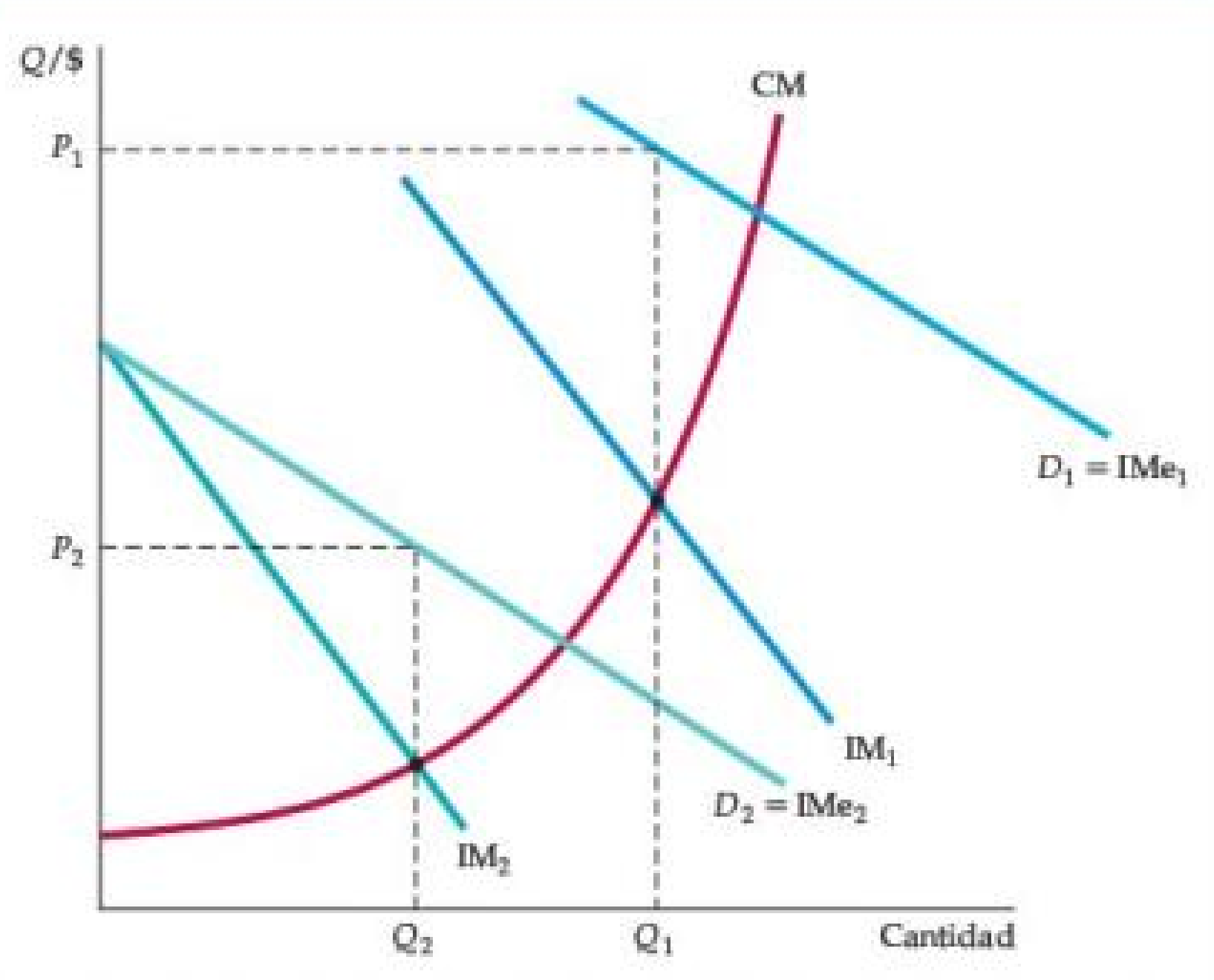
Figura: Fijación de Precios por Picos de Demanda
- Regla de decisión: en cada período t\in\{\text{peak},\text{valle}\}, elegir Q_t tal que IM_t(Q_t)=CM_t(Q_T).
(El CM_t puede diferir entre pico y valle por congestión/uso de capacidad.) - En la figura observamos lo siguiente:
- Línea roja: CM_t (más alto en pico).
- P_1 (línea horizontal superior): precio en pico; P_2 (línea inferior): precio en valle.
- Q_1 y Q_2: cantidades donde IM_t (curvas azules) corta a CM_t en cada período.
- Línea roja: CM_t (más alto en pico).
- Eficiencia: precios diferenciados racionan demanda en pico y desplazan consumo al valle, evitando producir con costos muy altos o sobredimensionar capacidad.
Tarifa de Dos Partes
Tarifa de dos partes: precio compuesto por tarifa de entrada (T) + tarifa de uso (P).
- La idea es fijar P basado en P=CM, lo que induce consumo eficiente; luego fijar T^* igual al excedente del consumidor a ese precio (T^*=EC(P=CM)) extrae todo el valor.
- Ejemplo (un consumidor): Un club deportivos con membresía + pago por hora de cancha de tenis.
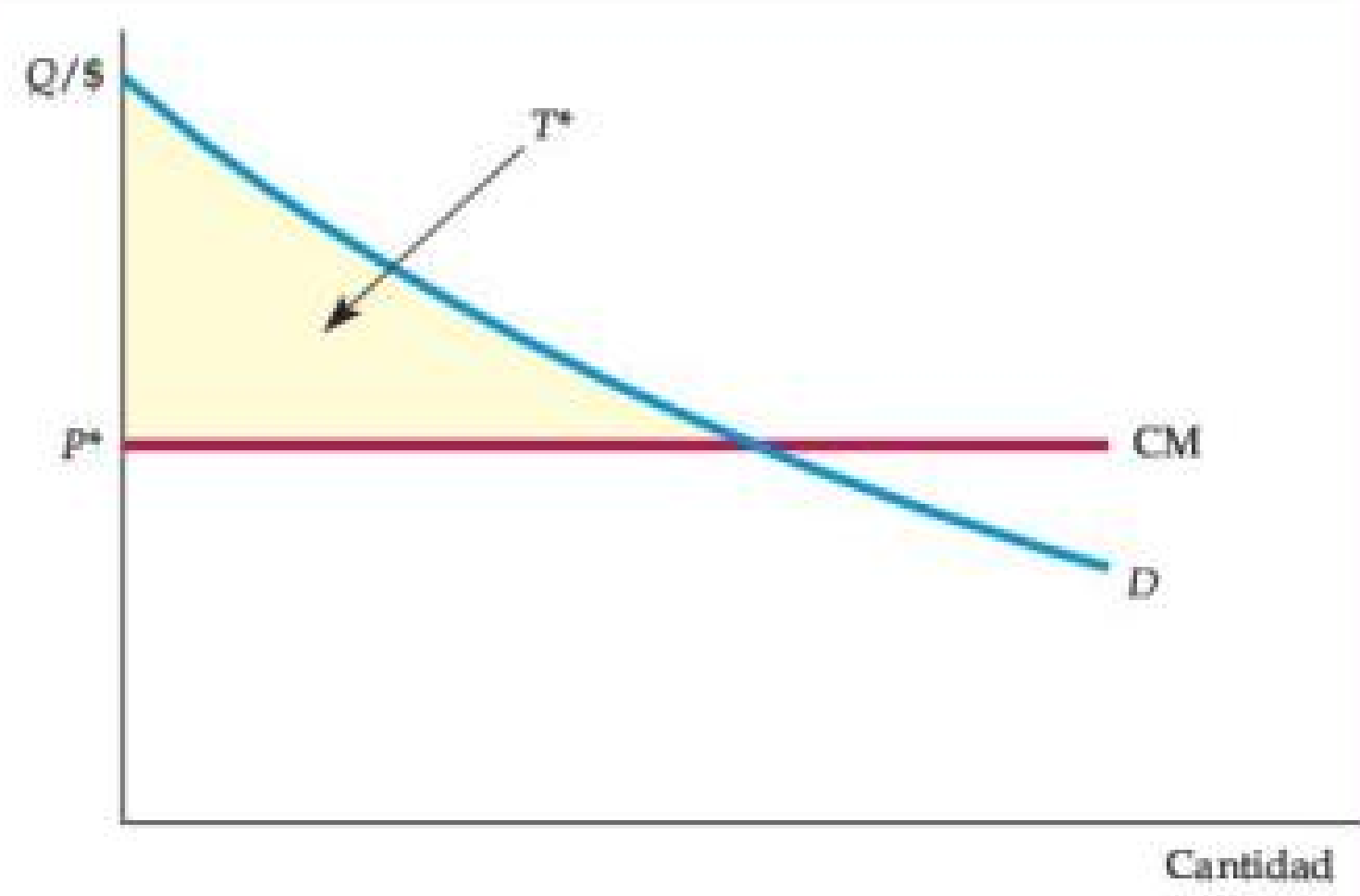
Figura: Tarifa de Dos Partes con un Solo Consumidor
- El consumidor tiene la curva de demanda D
- La empresa maximiza sus ganancias al fijar la tarifa de uso P igual al costo marginal y la tarifa de entrada T* igual al excedente total del consumidor.
- Óptimo: P=CM y T^\*=EC (área bajo D y sobre CM hasta Q^\*).
Tarifa de Dos Partes (dos consumidores)
Con heterogeneidad, conviene P^*>CM y fijar T igual al EC del consumidor con menor demanda para que ambos entren.
Trade-off: subir P aumenta margen por uso pero reduce el EC del tipo “débil”, forzando un T menor; la firma elige (P^*,T^*) que maximizan ganancias.
Ejemplos (con dos tipos): gimnasio con matrícula + copago por clase premium; móvil con cargo fijo + precio por GB/minuto.
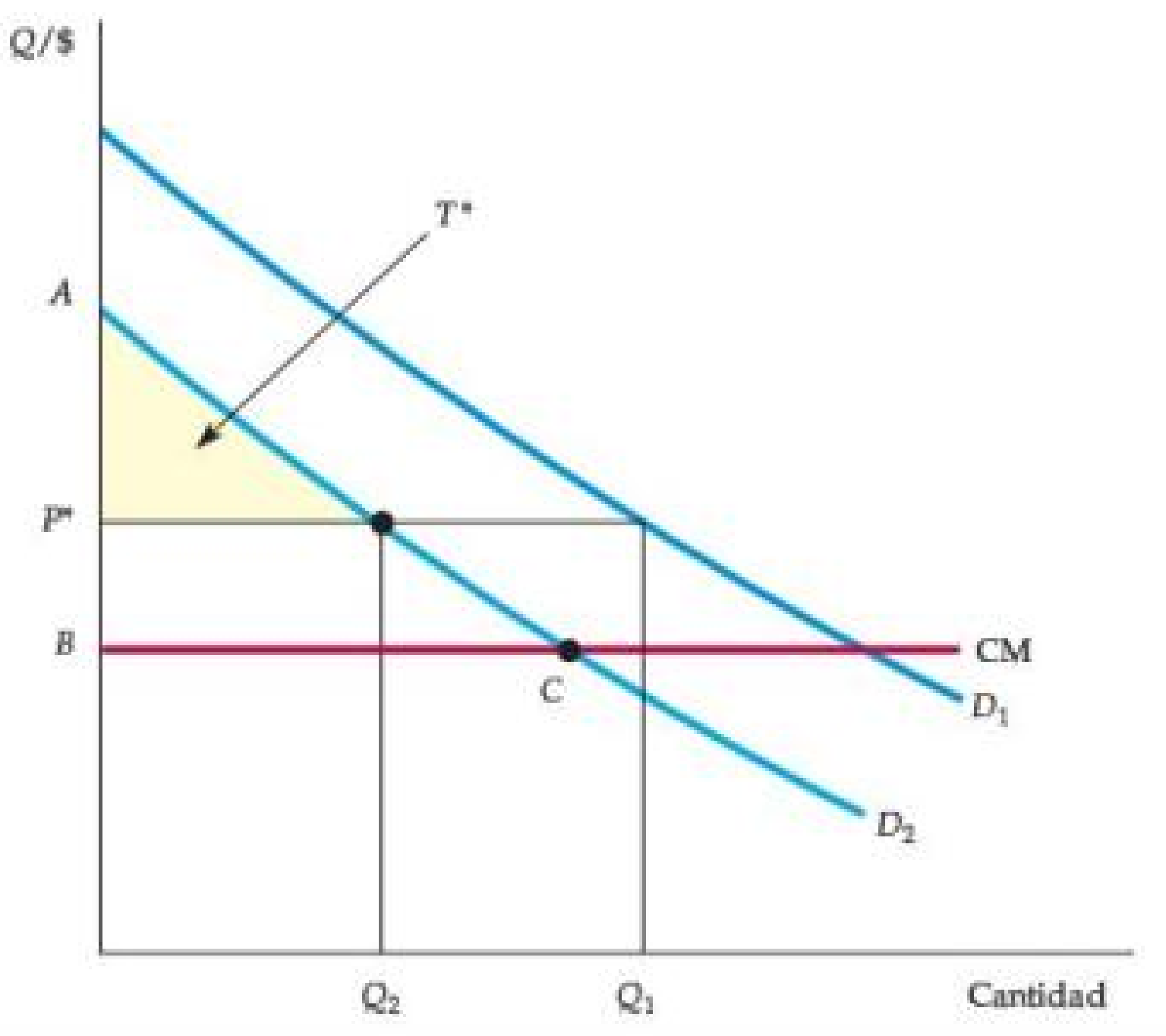
Figura: Tarifa de Dos Partes con Dos Consumidores
- T se fija por el EC del tipo con demanda D_2 (el más bajo).
- Ganancia: \pi=2T+(P^*-CM)(Q_1+Q_2) (con T común).
- En el gráfico: puntos negros en P^* sobre D_1 y D_2 definen (Q_1,Q_2); el triángulo ABC ilustra el EC del tipo débil que limita T.
Tarifa de Dos Partes (muchos consumidores)
Para la elección de P y T, planteamos el beneficio total \pi, que es la suma de la ganancia de la tarifa de entrada \pi_a y la ganancia de las ventas \pi_s. Tanto \pi_a como \pi_s dependen de T, la tarifa de entrada.
- Ejemplos (muchos consumidores): Servidores/cloud con tarifa base + cobro por uso (requests/GB); plataformas de movilidad con tarifa de reserva + precio por km/min.
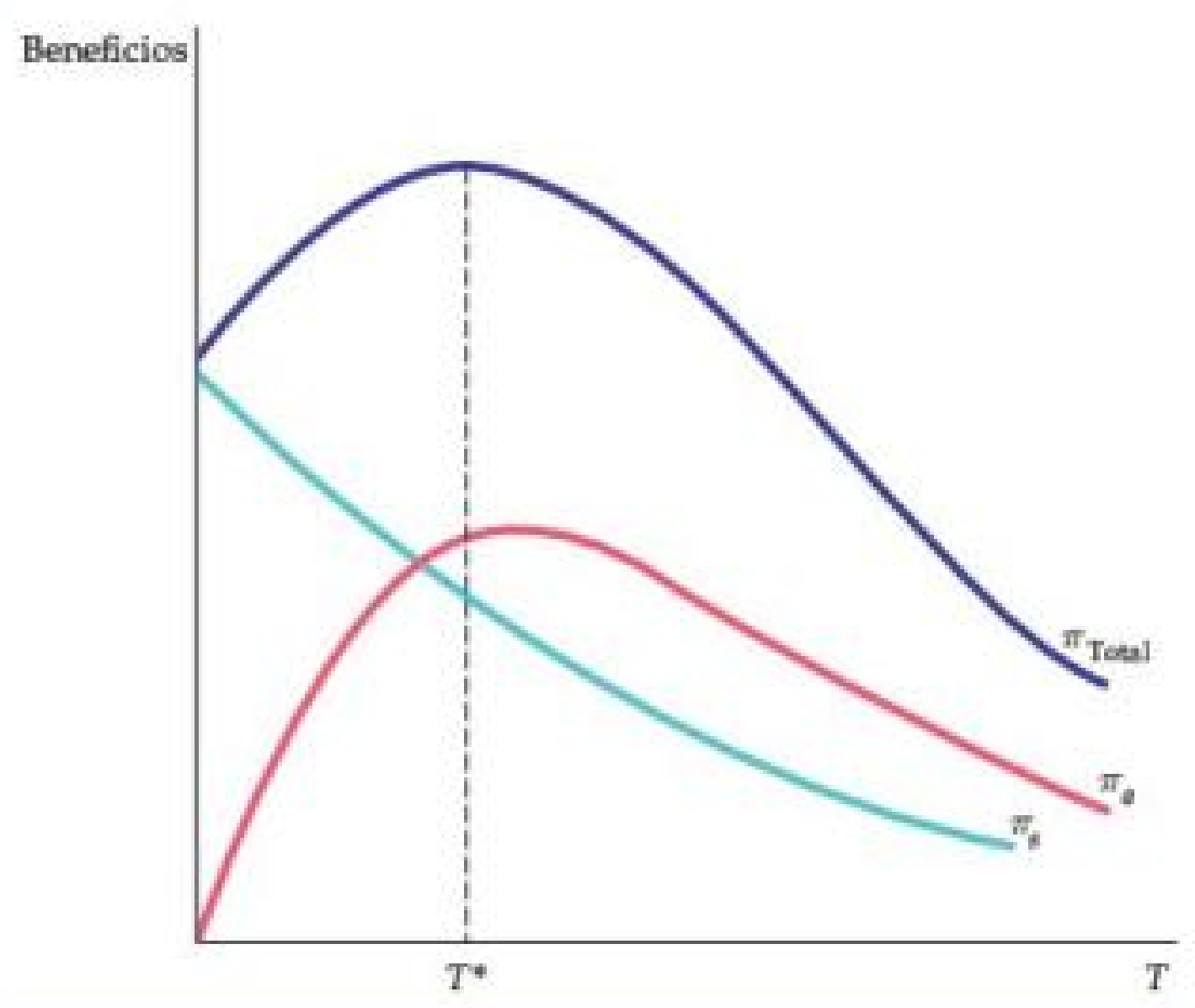
Figura: Tarifa de Dos Partes con Muchos Consumidores Diferentes \pi=\pi_a+\pi_s=n(T)\,T+\big(P-CM\big)\,Q\big(n(T)\big), donde n(T) es el número de entrantes (↓ con T) y Q(n) la venta total (↑ con n).
- Para cada P, existe un T^*(P) que maximiza \pi (curva morada \pi_{\text{Total}}); luego se ajusta P y se recalcula T^*(P).
- En el gráfico:
- \pi_a (acceso) crece con T y luego cae (expulsa usuarios).
- \pi_s (ventas) cae con T (menos uso).
- \pi_{\text{Total}} tiene un máximo interior en T^*.
- \pi_a (acceso) crece con T y luego cae (expulsa usuarios).
- T^* maximiza \pi dado P (línea vertical).
- Cambiar P desplaza todas las curvas y altera T^* y \pi.
Cierre
¿Preguntas?

\, O vía E-mail: luischanci@santotomas.cl