Competencia Monopolística y Oligopolio

Microeconomía

Prof. Luis Chancí

Introducción

• De la Competencia Perfecta al Monopolio
  Hemos visto hasta ahora los extremos del mercado: competencia perfecta, donde muchas empresas compiten sin poder de mercado, y el monopolio, donde una sola empresa controla toda la oferta.

• ¿Qué ocurre entre estos dos extremos?
  La competencia imperfecta incluye mercados donde las empresas tienen cierto grado de poder para fijar precios, pero enfrentan competencia.

• Competencia Imperfecta
  Competencia Monopolística: Muchas empresas compiten, pero cada una ofrece un producto diferenciado.
  Oligopolio: Unas pocas empresas dominan el mercado y sus decisiones están interrelacionadas.

• Importancia de Estudiar Competencia Imperfecta:
  Analizaremos cómo las empresas fijan precios y cantidades en mercados no competitivos.
  Entenderemos el impacto de la competencia versus colusión y cómo esto afecta el bienestar del consumidor.

• Uno de los Temas Clave
  Considerando que ahora habrá interacción entre agentes, partiremos por una breve introducción a Teoría de Juegos.
  El Dilema del Prisionero Ayudará a entender por qué, en mercados oligopólicos, las empresas pueden optar por competir agresivamente en lugar de colaborar, incluso cuando la cooperación resultaría en mayores beneficios para todas. Este concepto es clave para analizar comportamientos estratégicos como la fijación de precios y la formación de cárteles.

Contenidos de la unidad

0. Breve Introducción a Teoría de Juegos
1. Competencia Monopolística
2. Oligopolio
   2.1. Modelo de Cournot
   2.2. Modelo de Stackelberg
   2.3. Modelo de Bertrand
   
3. Competencia versus Colusión: El Dilema del Prisionero
   
4. Implicaciones del Dilema del Prisionero para la Fijación de Precios Oligopolísticos
   
5. Cárteles

0. Teoría de Juegos
\(\,\,\,\,\,\,\) (Breve Introducción)

Teoría de Juegos y Tipos de Equilibrio

Introducción y contexto

• Los individuos eligen el mejor resultado posible dadas las restricciones.
• A veces el resultado depende de las acciones de otros, así como de las propias acciones.
• ¿Cómo afecta esto la toma de decisiones?
• ¿Significa esto que las normas e instituciones importan?
• Las interacciones sociales pueden ayudar a explicar la Tragedia de los Comunes y dilemas sociales como el cambio climático.
• Usaremos un modelo de interacción social para explicar:
  • Situaciones en las que hay dos o más personas.
  • Las acciones de cada persona afectan tanto su propio resultado como el resultado de otras personas.

Teoría de Juegos y Tipos de Equilibrio

¿Qué es la Teoría de Juegos?

• La teoría de juegos es un conjunto de modelos de interacciones estratégicas.
• Cuando las personas participan en una interacción social y son conscientes de cómo sus acciones afectan a los demás y viceversa, lo llamamos una interacción estratégica.
• Una estrategia se define como una acción (o plan de acción) que una persona puede elegir mientras es consciente de la dependencia mutua de los resultados de sus propias acciones y las de los demás.

Teoría de Juegos y Tipos de Equilibrio

¿Qué es un Juego?

• Un juego es una descripción de una interacción social que especifica:
  • Los jugadores: Quién está interactuando con quién.
  • Las estrategias posibles: Qué acciones están disponibles para los jugadores.
  • El orden de juego: Cuándo los jugadores eligen sus acciones.
  • La información: Qué sabe cada jugador al tomar su decisión.
  • Los pagos: Cuáles serán los resultados para cada combinación posible de acciones.

Teoría de Juegos y Tipos de Equilibrio

Ejemplo de un Juego Simultáneo

• Supongamos hay dos agricultores, Luis y Chancí.
  • Se enfrentan a un problema: ¿deberían cultivar arroz o trigo?
  • Luis y Chancí pueden cultivar ambos tipos de cultivo, pero solo pueden cultivar uno a la vez.
  • Luis tiene tierras igualmente aptas para arroz y trigo. Chancí, sin embargo, tiene tierras buenas para arroz pero menos aptas para trigo.
  • Ambos venden sus cosechas en un mercado cercano. En el día de mercado, si llevan menos arroz, el precio será mayor. De igual manera, el precio del trigo depende de cuánto hayan producido.

Teoría de Juegos y Tipos de Equilibrio

Ejemplo de un Juego Simultáneo

Organización de la información y resultados en una matriz de pagos (Tabla que muestra las ganancias o pagos para cada empresa dada su decisión y la decisión de su competidor).

\[ \begin{array}{cc|ll} & & \text{Chancí}&\\ & & \text{Arroz} & \text{Trigo} \\ \hline \text{Luis} & \text{Arroz} & \text{Ambos producen arroz} & \text{Chancí no produce lo mejor en su tierra} \\ & & \text{Excedente de arroz (bajo precio)} & \text{Altos precios para ambos cultivos}\\ & & \text{Escasez de trigo} & \text{No hay escasez}\\ & & & \\ & \text{Trigo} & \text{Altos precios para ambos cultivos}& \text{Ambos producen trigo}\\ & & \text{No hay escasez} & \text{Excedente de trigo (bajo precio)}\\ & & & \text{Escasez de arroz}\\ & & & \text{Chancí no produce lo mejor en su tierra}\\ \end{array} \]

Teoría de Juegos y Tipos de Equilibrio

Ejemplo de un Juego Simultáneo

Organización de la información y resultados en una matriz de pagos (cont.).

\[ \left.\begin{array}{cc|ll} & & \text{Chancí}&\\ & & \text{Arroz} & \text{Trigo} \\ \hline \text{Luis} & \text{Arroz} & \text{Luis obtiene \$4} & \text{Luis obtiene \$6} \\ & & \text{Chancí obtiene \$4} & \text{Chancí obtiene \$3} \\ & & & \\ & \text{Trigo} & \text{Luis obtiene \$6} & \text{Luis obtiene \$5} \\ & & \text{Chancí obtiene \$6} & \text{Chancí obtiene \$2} \\ \end{array}\right\}\Rightarrow \]

\[ \,\\ \begin{array}{cc|ll} & & \text{Chancí}&\\ & & \text{Arroz} & \text{Trigo} \\ \hline \text{Luis} & \text{Arroz} & \text{( $4 ; $4 ) } & \text{ ( $6 ; $3 ) } \\ & \text{Trigo} & \text{( $6 ; $6 ) } & \text{ ( $5 ; $2 ) } \\ \end{array} \]

Teoría de Juegos y Tipos de Equilibrio

Tipos de Equilibrio

• En un juego, el equilibrio puede ser de diferentes tipos según las estrategias elegidas.
• Equilibrio de Nash: Un conjunto de estrategias en el que cada jugador elige la mejor respuesta a las estrategias de los demás.

Encontrando las Mejores Respuestas

• Al analizar la matriz de pagos, se puede identificar la mejor respuesta de cada jugador.
• El concepto de mejor respuesta es clave para encontrar el equilibrio de Nash.

Teoría de Juegos y Tipos de Equilibrio

Equilibrio de Nash

• En teoría de juegos, un conjunto de estrategias en el que cada jugador juega su mejor respuesta a las estrategias de los demás se llama equilibrio de Nash.
• En el equilibrio de Nash del ejemplo de los agricultores:
  • Luis elige cultivar trigo.
  • Chancí elige cultivar arroz.

Equilibrio de Estrategia Dominante

• Si la mejor respuesta de un jugador es siempre la misma estrategia, independientemente de la estrategia del otro jugador, se dice que es la estrategia dominante de ese jugador.
• Un equilibrio de estrategia dominante se da cuando ambos jugadores eligen sus estrategias dominantes.

Más adelante volveremos a teoría de juegos mediante el Dilema del Prisionero.

Teoría de Juegos y Tipos de Equilibrio

La película Una Mente Brillante ( A Beautiful Mind , 2001) trata sobre la vida del matemático estadounidense John Forbes Nash , ganador del Premio Nobel de Economía en 1994.

El siguiente extracto es de la parte que ` intenta ’ ilustrar el Equilibrio de Nash:

Fuente: kidVB (2007). Nash Equilibrium. YouTube. https://www.youtube.com/watch?v=2d_dtTZQyUM

1. Competencia Monopolística

Definición

Competencia monopolística: Mercado en el que las empresas pueden entrar libremente, cada una produciendo su propia marca o versión de un producto diferenciado.

Competencia Monopolística

Las Bases de la Competencia Monopolística

Un mercado de competencia monopolística tiene dos características clave:

1. Las empresas compiten vendiendo productos diferenciados que son altamente sustituibles entre sí, pero no son sustitutos perfectos. En otras palabras, las elasticidades cruzadas de la demanda son grandes pero no infinitas.
2. Hay entrada y salida libres: es relativamente fácil para las nuevas empresas entrar al mercado con sus propias marcas y para las empresas existentes salir si sus productos se vuelven no rentables.

Competencia Monopolística: Corto y Largo Plazo

Equilibrio a Corto y Largo Plazo

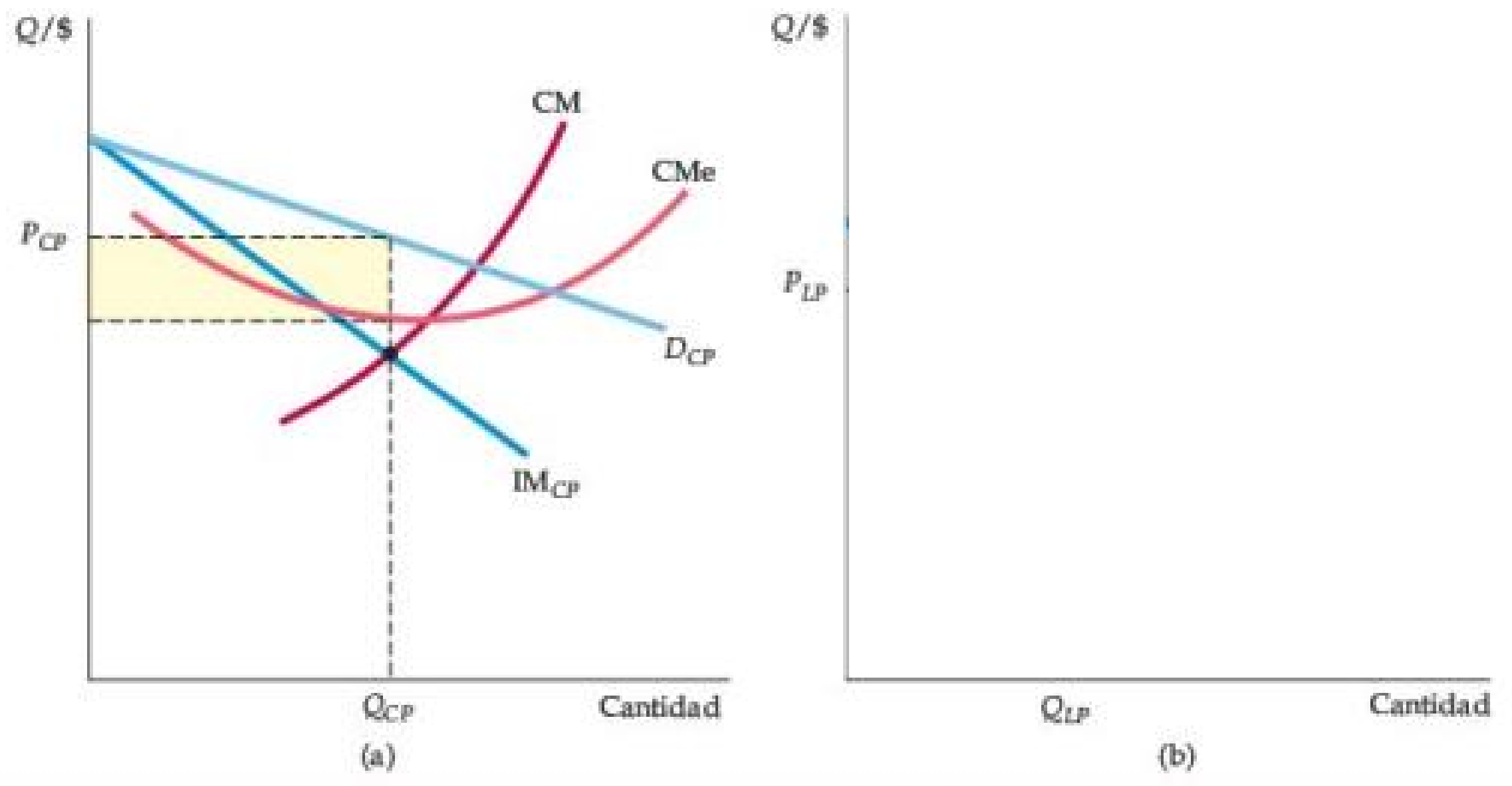
Figura: Una firma en competencia monopolística en el corto y largo plazo

• Debido a que la empresa es la única productora de su marca, enfrenta una curva de demanda con pendiente negativa.
• El precio excede el costo marginal y la empresa tiene poder de monopolio.
• En el corto plazo, descrito en la parte (a), el precio también excede el costo promedio y la empresa obtiene ganancias mostradas por el rectángulo sombreado en amarillo.

Competencia Monopolística: Corto y Largo Plazo

Equilibrio a Corto y Largo Plazo (cont.)

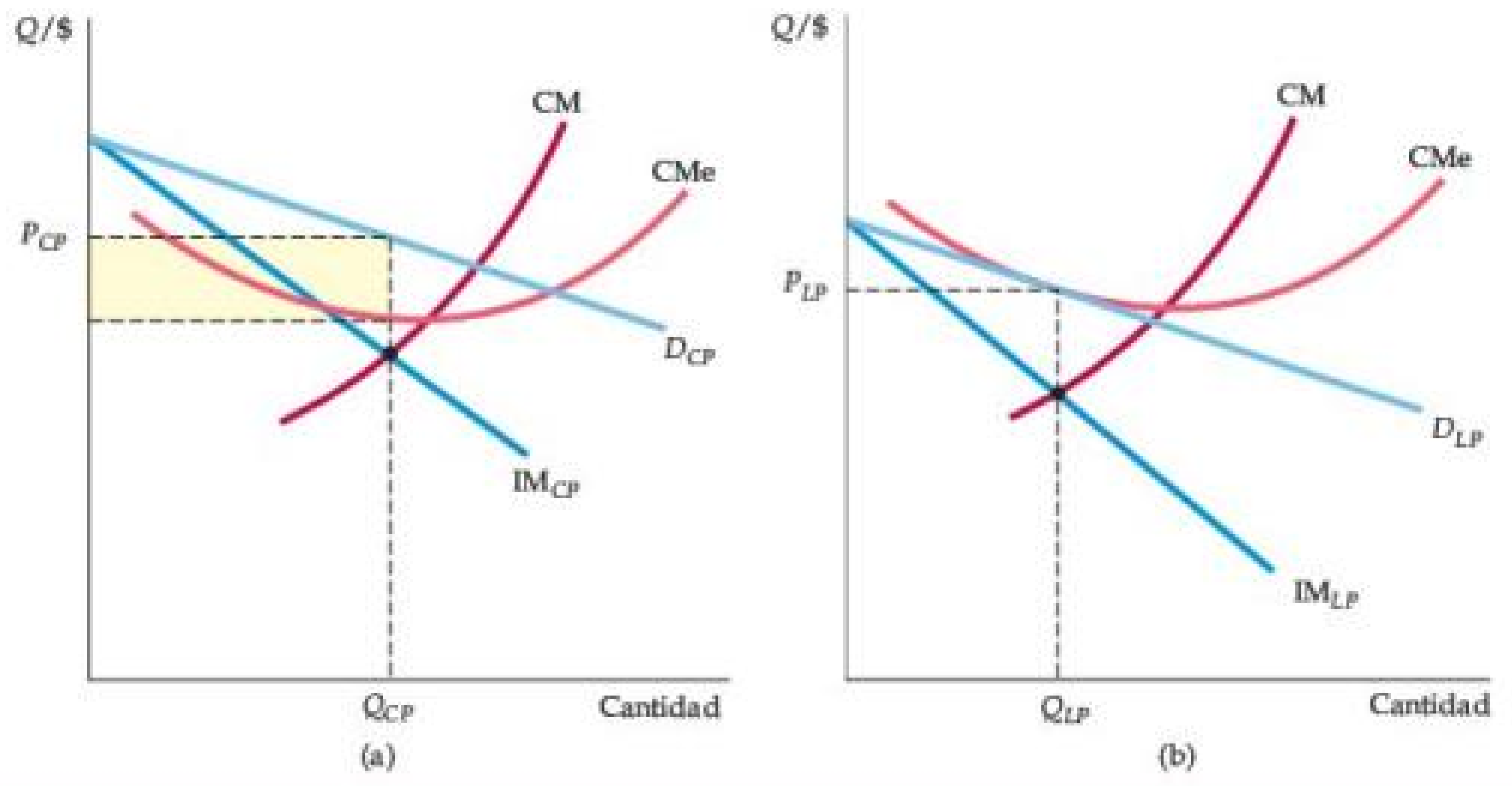
Figura: Una firma en competencia monopolística en el corto y largo plazo (cont.)

• A largo plazo, estas ganancias atraen a nuevas empresas con marcas competidoras. La cuota de mercado de la empresa disminuye y su curva de demanda se desplaza hacia abajo.
• En el equilibrio a largo plazo, descrito en la parte (b), el precio iguala al costo promedio, por lo que la empresa no obtiene ganancias, aunque tiene poder de monopolio.

Competencia Monopolística

Competencia Monopolística y Eficiencia Económica

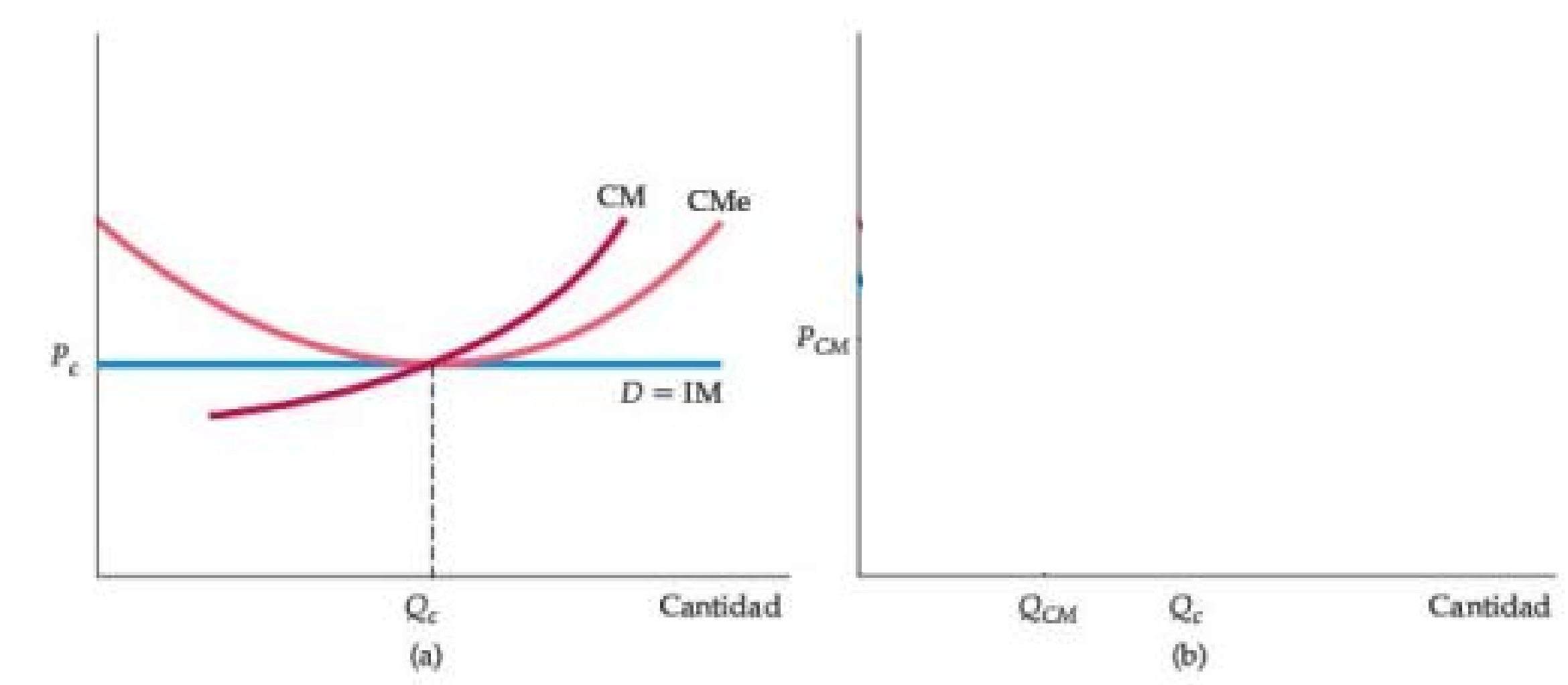
Figura: Comparación del equilibrio de competencia monopolística y competencia perfecta

• Bajo competencia perfecta, el precio iguala al costo marginal.
• La curva de demanda que enfrenta la empresa es horizontal, por lo que el punto de ganancia cero ocurre en el punto de costo promedio mínimo.

Competencia Monopolística

Competencia Monopolística y Eficiencia Económica

Figura: Comparación del equilibrio de competencia monopolística y competencia perfecta (continuación)

• Bajo competencia monopolística, el precio excede al costo marginal.
• Por lo tanto, hay una pérdida irrecuperable, como se muestra en el área sombreada en amarillo.
• La curva de demanda tiene pendiente negativa, por lo que el punto de ganancia cero está a la izquierda del punto de costo promedio mínimo.

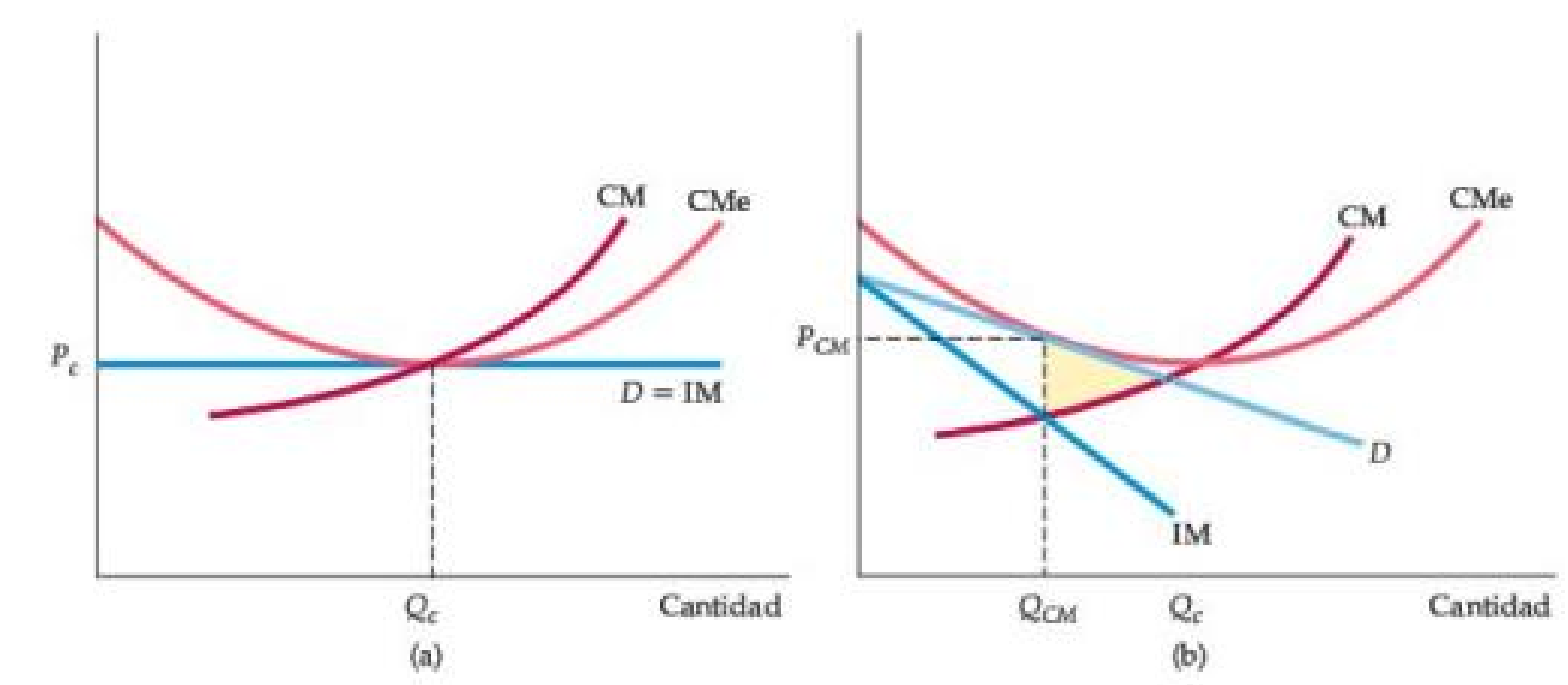
En ambos tipos de mercados, la entrada ocurre hasta que las ganancias se reducen a cero. Al evaluar la competencia monopolística, estas ineficiencias deben equilibrarse con los beneficios para los consumidores de la diversidad de productos.

2. Oligopolio

Definición

Oligopolio: Mercado en el que solo unas pocas empresas compiten entre sí y la entrada de nuevas empresas está impedida.

Oligopolio: Bases

Las Bases del Oligopolio

• En los mercados oligopolísticos, los productos pueden o no estar diferenciados.
• Lo que importa es que solo unas pocas empresas representan la mayor parte o toda la producción total.
• En algunos mercados oligopolísticos, algunas o todas las empresas obtienen ganancias sustanciales a largo plazo porque las barreras de entrada hacen que sea difícil o imposible para nuevas empresas entrar.
• El oligopolio es una forma prevalente de estructura de mercado. Ejemplos de industrias oligopolísticas incluyen automóviles, acero, aluminio, petroquímicos, equipos eléctricos y computadoras.

Oligopolio: Equilibrio

Equilibrio en un Mercado Oligopolístico

Cuando un mercado está en equilibrio, las empresas están haciendo lo mejor que pueden y no tienen razón para cambiar su precio o producción.

• equilibrio de Nash: Conjunto de estrategias o acciones en las que cada empresa hace lo mejor que puede dadas las acciones de sus competidores.
• duopolio: Mercado en el que dos empresas compiten entre sí.

Oligopolio: Modelo de Cournot

El Modelo de Cournot

• modelo de Cournot: Modelo de oligopolio en el que las empresas producen un bien homogéneo, cada empresa trata la producción de sus competidores como fija y todas las empresas deciden simultáneamente cuánto producir.

Oligopolio: Modelo de Cournot (cont.)

El Modelo de Cournot (cont.)

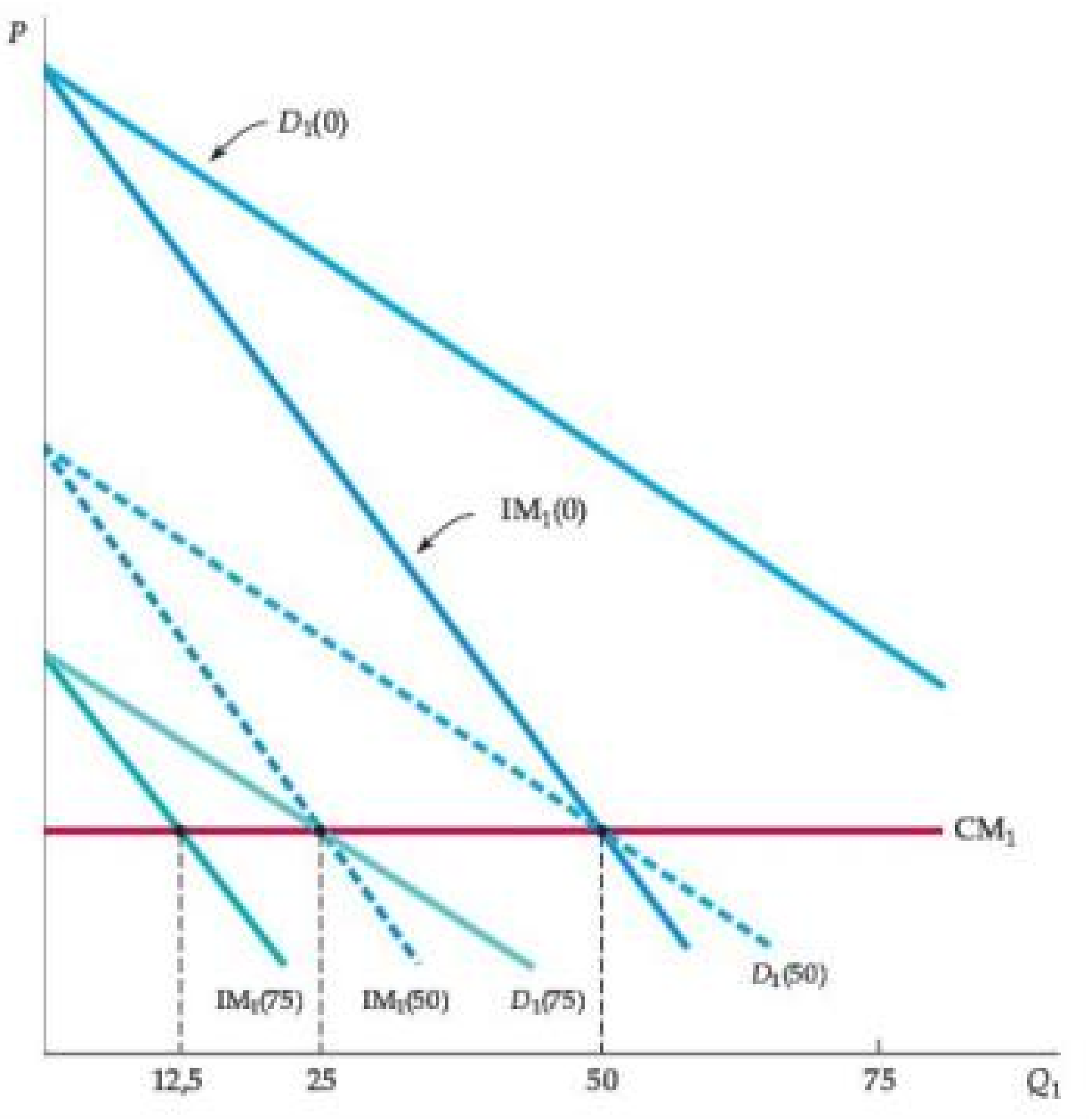
Figura: Decisión de producción de la Empresa 1

• La producción que maximiza las ganancias de la Empresa 1 depende de cuánto piense que producirá la Empresa 2.
• Si piensa que la Empresa 2 no producirá nada, su curva de demanda etiquetada D1(0) es la curva de demanda del mercado. La correspondiente curva de ingreso marginal etiquetada MR1(0) se intersecta con la curva de costo marginal de la Empresa 1 MC1 en una producción de 50 unidades.
• Si la Empresa 1 piensa que la Empresa 2 producirá 50 unidades, su curva de demanda D1(50) se desplaza hacia la izquierda en esta cantidad. La maximización de ganancias ahora implica una producción de 25 unidades.
• Finalmente, si la Empresa 1 piensa que la Empresa 2 producirá 75 unidades, la Empresa 1 producirá solo 12.5 unidades.

Oligopolio: Modelo de Cournot (cont.)

El Modelo de Cournot

• curva de reacción: Relación entre la producción que maximiza las ganancias de una empresa y la cantidad que piensa que su competidor producirá.
• equilibrio de Cournot: Equilibrio en el modelo de Cournot en el que cada empresa asume correctamente cuánto producirá su competidor y establece su propio nivel de producción en consecuencia.

Oligopolio: Modelo de Cournot (cont.)

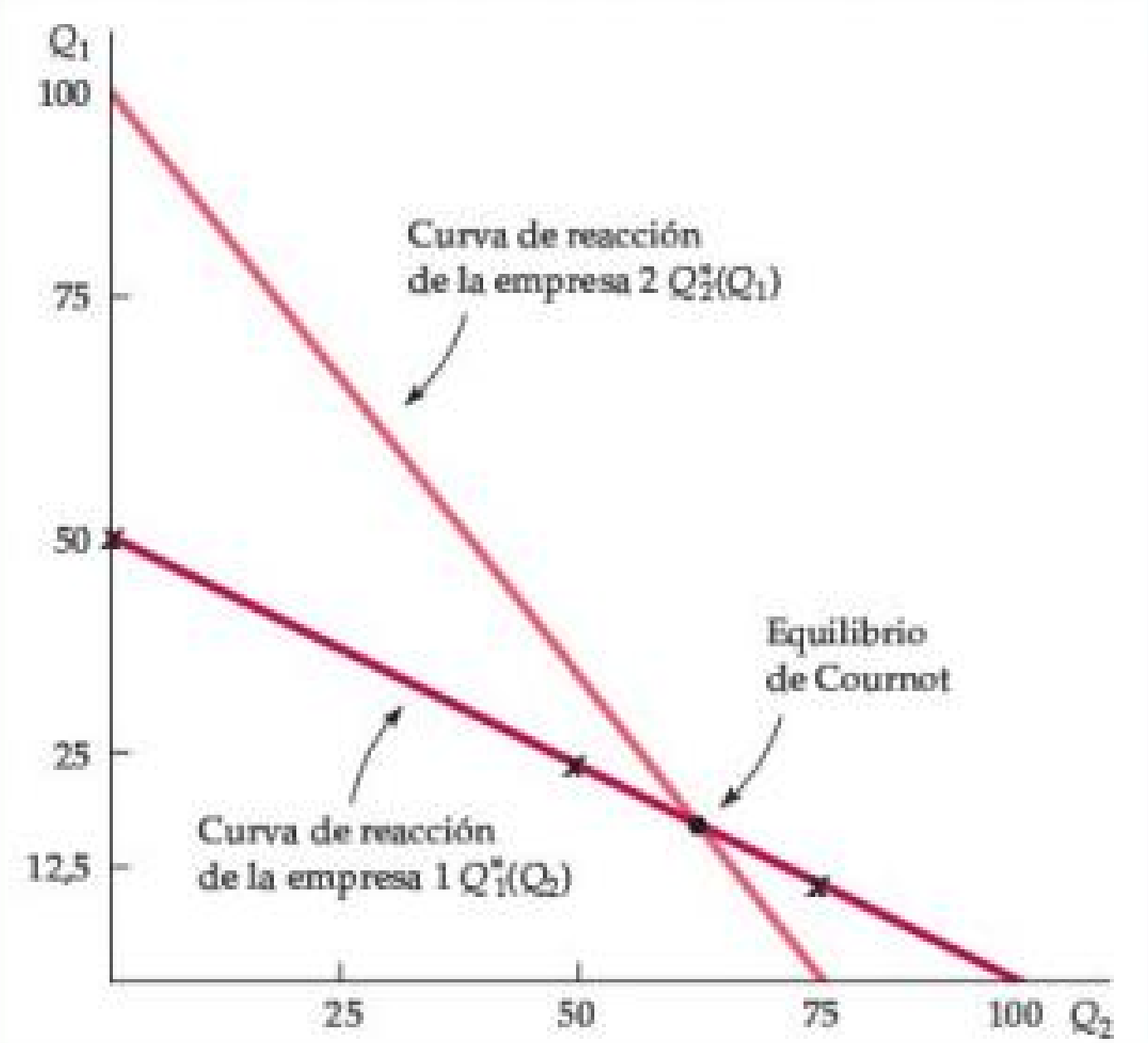
Figura: Curvas de reacción y equilibrio de Cournot

• La curva de reacción de la Empresa 1 muestra cuánto producirá en función de cuánto piense que producirá la Empresa 2.
• La curva de reacción de la Empresa 2 muestra su producción en función de cuánto piense que producirá la Empresa 1.
• En el equilibrio de Cournot, cada empresa asume correctamente la cantidad que producirá su competidor y, por lo tanto, maximiza sus propias ganancias. Por lo tanto, ninguna empresa se moverá de este equilibrio.

Oligopolio: Modelo de Cournot - Ejemplo

Los duopolistas enfrentan la demanda del mercado: \[ P=30-Q,\quad Q=Q_1+Q_2, \qquad CM_1=CM_2=0 \]

El ingreso total para la Empresa 1: \[ I_1 = P\cdot Q_1 = (30 - Q)Q_1 \] entonces \[ IM_1 = \Delta I_1 / \Delta Q_1 = 30 - 2Q_1 - Q_2 \] Curvas de reacción (igualando (IM_i=CM_i)): \[ Q_1=15-\tfrac{1}{2}Q_2, \qquad Q_2=15-\tfrac{1}{2}Q_1. \]

Equilibrio de Cournot: \(Q_1=Q_2=10 \Rightarrow Q= Q1 + Q2=20\) y \[ P=30-Q=10. \]

Oligopolio: Modelo de Cournot - Ejemplo

Si las dos empresas coluden, entonces la cantidad total que maximiza las ganancias se puede obtener de la siguiente manera:

El ingreso total para las dos empresas: \[ I = P\cdot Q = (30 - Q)Q = 30Q - Q^2 \] Por ende, \[ IM = \Delta I / \Delta Q = 30 - 2Q \] Al hacer \(IM=CM = 0\), encontramos que la ganancia total se maximiza en \[Q = 15\] Así, \[ Q_1 + Q_2 = 15 \] es la curva de colusión.

Si las empresas acuerdan compartir las ganancias por igual, cada una producirá la mitad de la producción total: \[ Q_1 = Q_2 = 7,5 \]

Oligopolio: Modelo de Cournot - Ejemplo

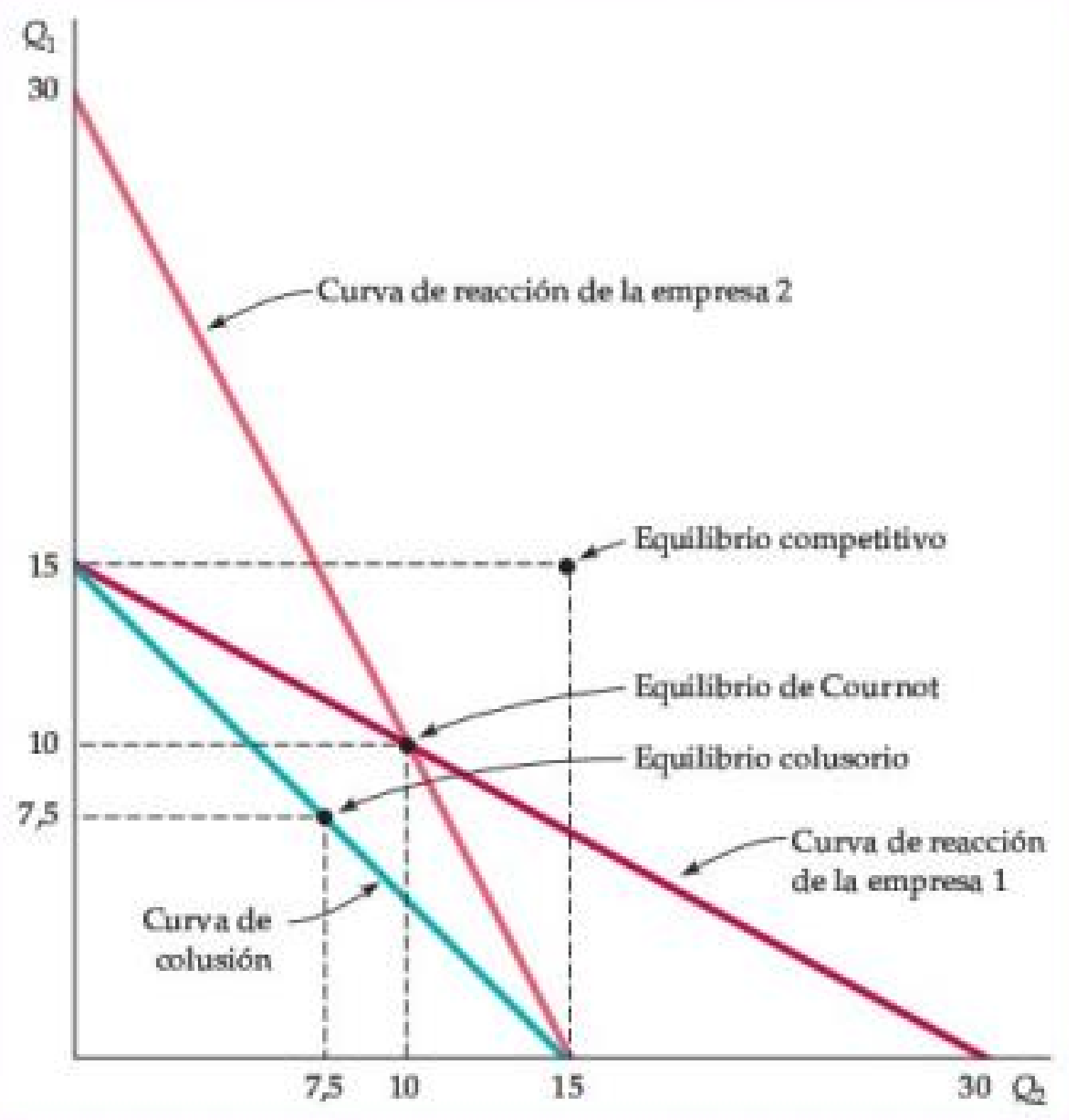
Figura: Ejemplo de duopolio

• Demanda \(P=30-Q\) y \(CM_1=CM_2=0\).
  En Cournot, \(Q_1=Q_2=10\) \(\Rightarrow\) \(Q=20\).
  
• Precio de equilibrio: \(P=10\).
  
• La curva de colusión muestra combinaciones de \(Q_1\) y \(Q_2\) que maximizan las ganancias totales.
• Si las empresas coluden y comparten las ganancias por igual, cada una producirá 7,5.
• También se muestra el equilibrio competitivo con \(P=CM\) y ganancia cero.

Oligopolio: Modelo de Stackelberg

\[\,\]

Ventaja del Primer Mover - El Modelo de Stackelberg (líder-seguidor)

\[\,\]

modelo de Stackelberg: Modelo de oligopolio en el que una empresa establece su producción antes que las demás.

Oligopolio: Modelo de Stackelberg - Ejemplo

Supongamos que la Empresa 1 mueve primero (es decir, establece su producción primero) y la Empresa 2 reacciona (después de observar la producción de la Empresa 1).

Al establecer la producción, la Empresa 1 debe considerar cómo reaccionará la Empresa 2,

\[ P=30-Q,\quad CM_1=CM_2=0,\quad \text{reacción de 2: }\, Q_2=15-\tfrac{1}{2}Q_1 \]

El ingreso de la Empresa 1 es \(I_1 = PQ_1=30Q_1 - Q_1^2 - 15Q_1\), y por ende, \[IM_1 = \Delta I_1 / \Delta Q_1 = 15 - Q_1\]

Estableciendo \(IM_1 =CM= 0\), se obtiene \(Q_1 = 15\) y \(Q_2 = 7,5\).

Las ganancias son: \(\pi_1=P Q_1=112{,}5\), \(\pi_2=P Q_2=56{,}25\).

Por ende, concluimos que la Empresa 1 produce el doble que la Empresa 2 y obtiene el doble de ganancia. Ir primero le da una ventaja a la Empresa 1.

Oligopolio: Modelo de Bertrand (Competencia de Precios)

\[\,\]

Competencia de Precios con Productos Homogéneos - El Modelo de Bertrand

\[\,\]

Modelo de Bertrand: Modelo de oligopolio en el que las empresas producen un bien homogéneo, cada empresa trata el precio de sus competidores como fijo y todas las empresas deciden simultáneamente qué precio cobrar.

Oligopolio: Modelo de Bertrand (Competencia de Precios)

En el ejemplo con \[P = 30 - Q\] \[MC_1 = MC_2 = \$3\]

• Se tiene que:

  • En equilibrio de Cournot, la cantidad producida por cada empresa es: \(Q_1 = Q_2 = 9\) y el precio de mercado es $12, por lo que cada empresa obtiene una ganancia de $81.

  • El equilibrio de Nash en el modelo de Bertrand resulta en ambas empresas estableciendo el precio igual al costo marginal: \(P1 = P2 = \$3\). Entonces, la producción total de la industria es de 27 unidades, de las cuales cada empresa produce 13.5 unidades y ambas empresas obtienen una ganancia cero.

  • En el modelo de Cournot, debido a que cada empresa produce solo 9 unidades, el precio de mercado es $12.

  • Ahora, el precio de mercado es $3. En el modelo de Cournot, cada empresa obtenía una ganancia; en el modelo de Bertrand, las empresas fijan el precio al costo marginal y no obtienen ganancias.

Competencia de Precios con Productos Diferenciados

Ejemplo

Supongamos que cada uno de los dos duopolistas tiene costos fijos de 20, pero costos variables cero, y que enfrentan las siguientes (mismas) curvas de demanda: \[ Q_1=12-2P_1+P_2,\qquad Q_2=12-2P_2+P_1. \]

En este caso, cada empresa selecciona precios maximizando beneficios, \(\pi_1=P_1Q_1-20\) y \(\pi_2=P_2Q_2-20\).

Por ende, al determinar el precio que maximiza las ganancias de cada empresa (conocido como mejor respuesta o Best Response ): \[ \text{BR}_1:\; P_1=3+\tfrac{1}{4}P_2,\qquad \text{BR}_2:\; P_2=3+\tfrac{1}{4}P_1. \] Posibles soluciones son:

• Equilibrio de Nash (simétrico): \(P_1=P_2=4\).
• Precio colusivo simétrico: Maximiza \(\Pi=P(Q_1+Q_2)=P(24-3P)\Rightarrow P=6\).

Competencia de Precios con Productos Diferenciados

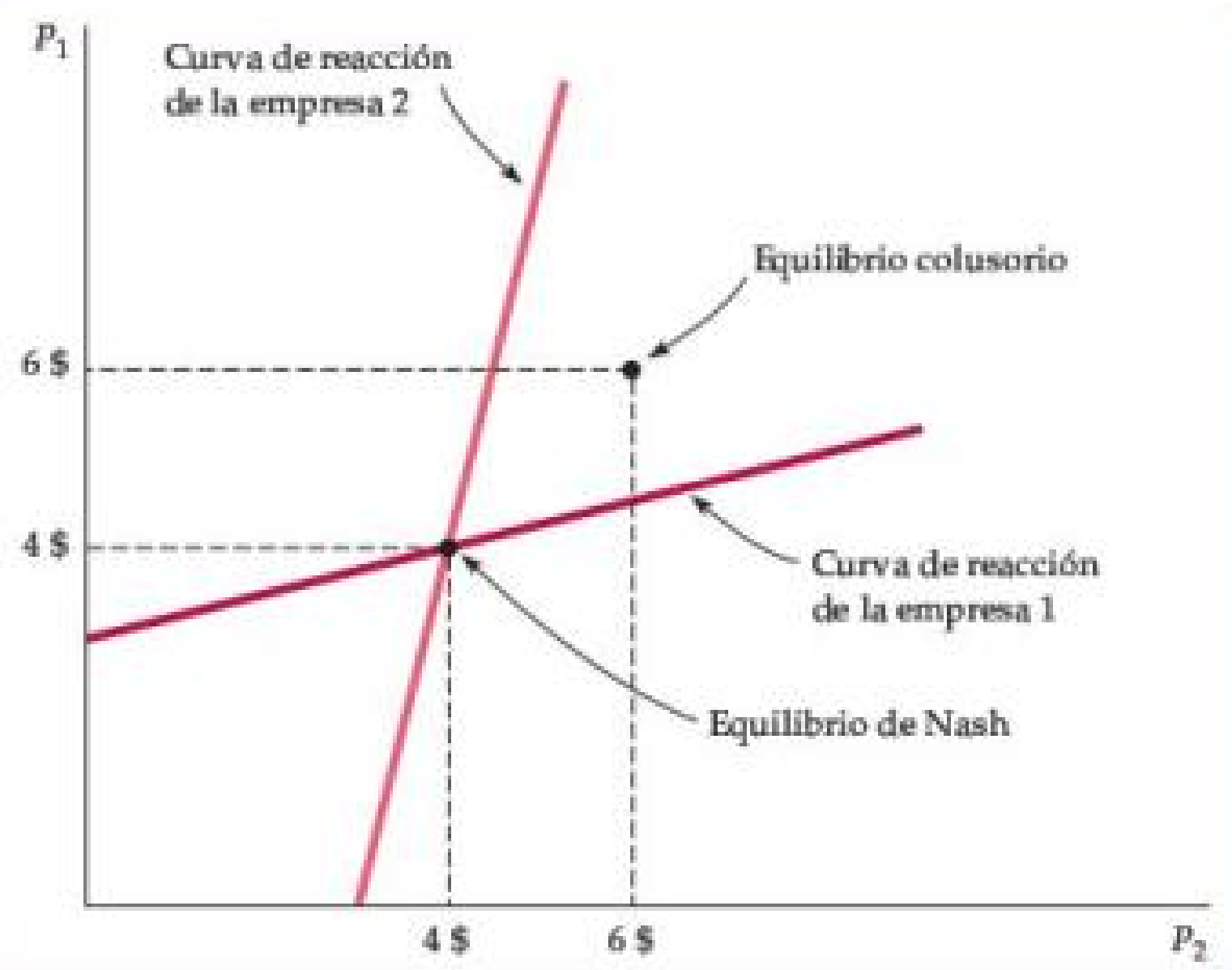
Figura: Equilibrio de Nash en Precios

• Dos empresas venden productos diferenciados y la demanda de cada empresa depende tanto de su propio precio como del precio de su competidor, \(Q_i=12-2P_i+P_j\).
• Las dos empresas eligen sus precios al mismo tiempo, tomando cada una el precio de su competidor como dado.
• La curva de reacción de la Empresa 1 da su precio que maximiza las ganancias como una función del precio que establece la Empresa 2, \(P_1=3+\tfrac{1}{4}P_2\). De manera similar, para la Empresa 2, la curva de reacción es \(P_2=3+\tfrac{1}{4}P_1\).
• Equilibrio de Nash está en la intersección de las dos curvas de reacción, \(P_1=P_2=4\). Es decir, cuando cada empresa cobra un precio de $4, está haciendo lo mejor que puede dado el precio de su competidor y no tiene incentivos para cambiar el precio.
• También se muestra el equilibrio en colusión (simétrica) (es decir, si las empresas fijan cooperativamente el precio), \(P_1=P_2=6\).

3. Competencia versus Colusión:
\(\,\,\,\,\,\,\) El Dilema del Prisionero

Competencia versus Colusión: El Dilema del Prisionero

En nuestro ejemplo: costos variables cero y demandas \[ Q_1=12-2P_1+P_2,\qquad Q_2=12-2P_2+P_1. \]

• En Nash, \(P_1=P_2=4\Rightarrow \pi_1=\pi_2=12\).
• En colusión simétrica, \(P_1=P_2=6\Rightarrow \pi_1=\pi_2=16\).
• Si 1 cobra 6 y 2 desvía a 4: \(\pi_2=(4)\,[12-2(4)+6]-20=20\), \(\pi_1=(6)\,[12-2(6)+4]-20=4\).

\[ \begin{array}{cc|cc} & & \text{Empresa 2}&\\ & & \text{Cobrar \$4} & \text{Cobrar \$6} \\ \hline \text{Empresa 1} & \text{Cobrar \$4} & (12 \text{,} 12) & (20 \text{,} 4) \\ & \text{Cobrar \$6} & (4 , 20) & (16 , 16) \\ \end{array} \]

Competencia versus Colusión: El Dilema del Prisionero

Matriz de Pagos

• juego no cooperativo: Juego en el que la negociación y la aplicación de contratos vinculantes no son posibles.

El Dilema del Prisionero

• dilema del prisionero: Ejemplo de teoría de juegos en el que dos prisioneros deben decidir por separado si confiesan un crimen; si un prisionero confiesa, recibirá una sentencia más leve y su cómplice recibirá una más pesada, pero si ninguno confiesa, las sentencias serán más leves que si ambos confiesan.

\[ \begin{array}{cc|cc} & & \text{Prisionero B}&\\ & & \text{Confesar} & \text{No confesar} \\ \hline \text{Prisionero A} & \text{Confesar} & (-5 \text{;} -5) & (-1 \text{;} -10) \\ & \text{No confesar} & (-10 ; -1) & (-2 ; -2) \\ \end{array} \]

4. Implicaciones del Dilema del Prisionero

Implicaciones del Dilema del Prisionero

Rigidez de Precios

• rigidez de precios: Característica de los mercados oligopolísticos por la cual las empresas son reacias a cambiar los precios incluso si los costos o la demanda cambian.
• modelo de la curva de demanda quebrada: Modelo de oligopolio en el que cada empresa enfrenta una curva de demanda quebrada en el precio prevaleciente: a precios más altos, la demanda es muy elástica, mientras que a precios más bajos, es inelástica.

Implicaciones del Dilema del Prisionero

Rigidez de Precios

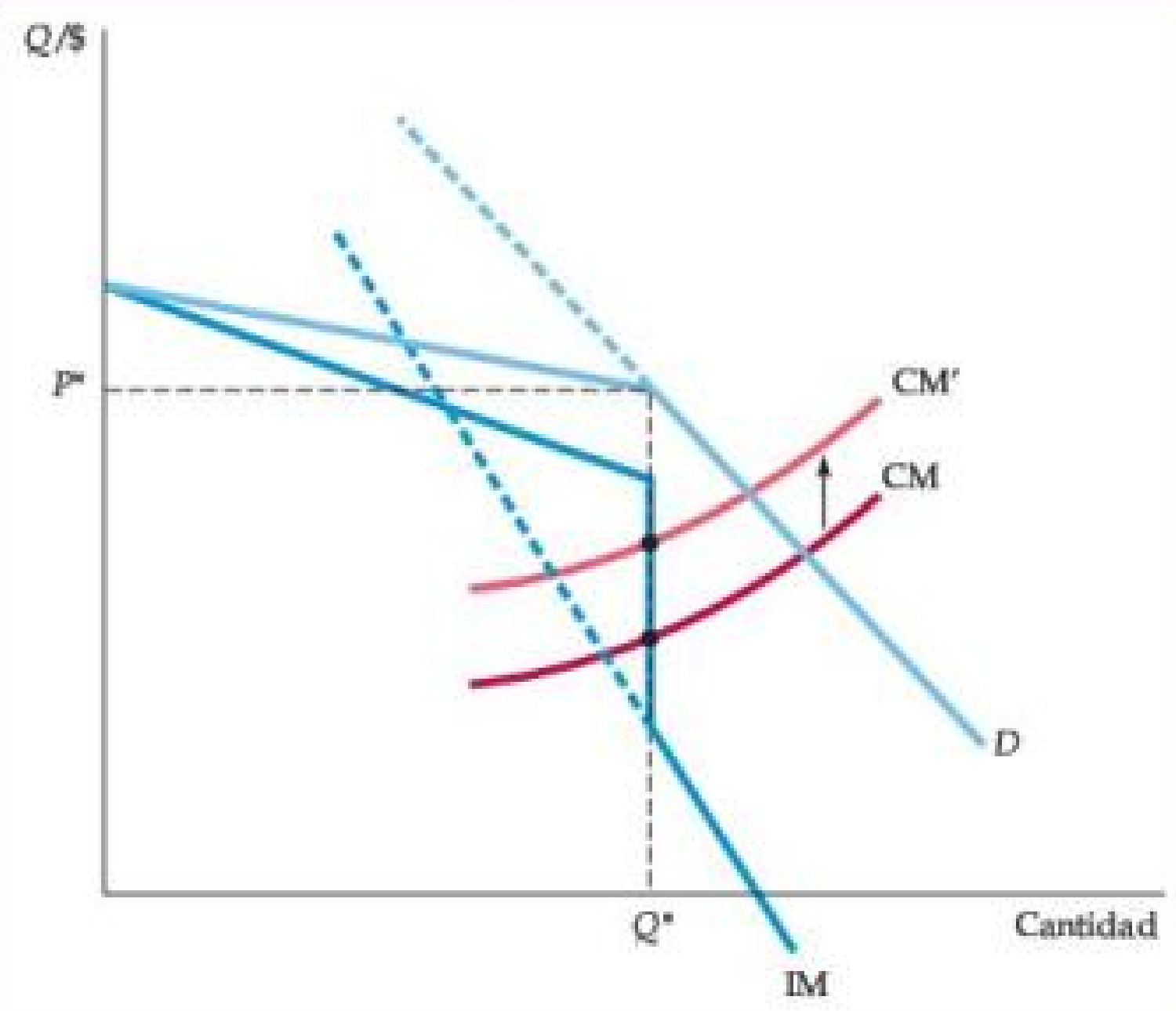
Figura: La Curva de Demanda Quebrada

• Cada empresa cree que si aumenta su precio por encima del precio actual P* , ninguno de sus competidores seguirá su ejemplo, por lo que perderá la mayoría de sus ventas.
• Cada empresa también cree que si baja el precio, todos seguirán su ejemplo y sus ventas solo aumentarán en la medida en que aumente la demanda del mercado.
• Como resultado, la curva de demanda de la empresa D está quebrada en el precio P* y su curva de ingreso marginal MR es discontinua en ese punto.
• Si el costo marginal aumenta de MC a MC’, la empresa aún producirá el mismo nivel de producción Q* y cobrará el mismo precio P* .

Implicaciones del Dilema del Prisionero

Señalización de Precios y Liderazgo de Precios

• señalización de precios: Forma de colusión implícita en la que una empresa anuncia un aumento de precios con la esperanza de que otras empresas sigan su ejemplo.
• liderazgo de precios: Patrón de fijación de precios en el que una empresa anuncia regularmente cambios de precios que otras empresas luego igualan.

Implicaciones del Dilema del Prisionero

El Modelo de la Empresa Dominante

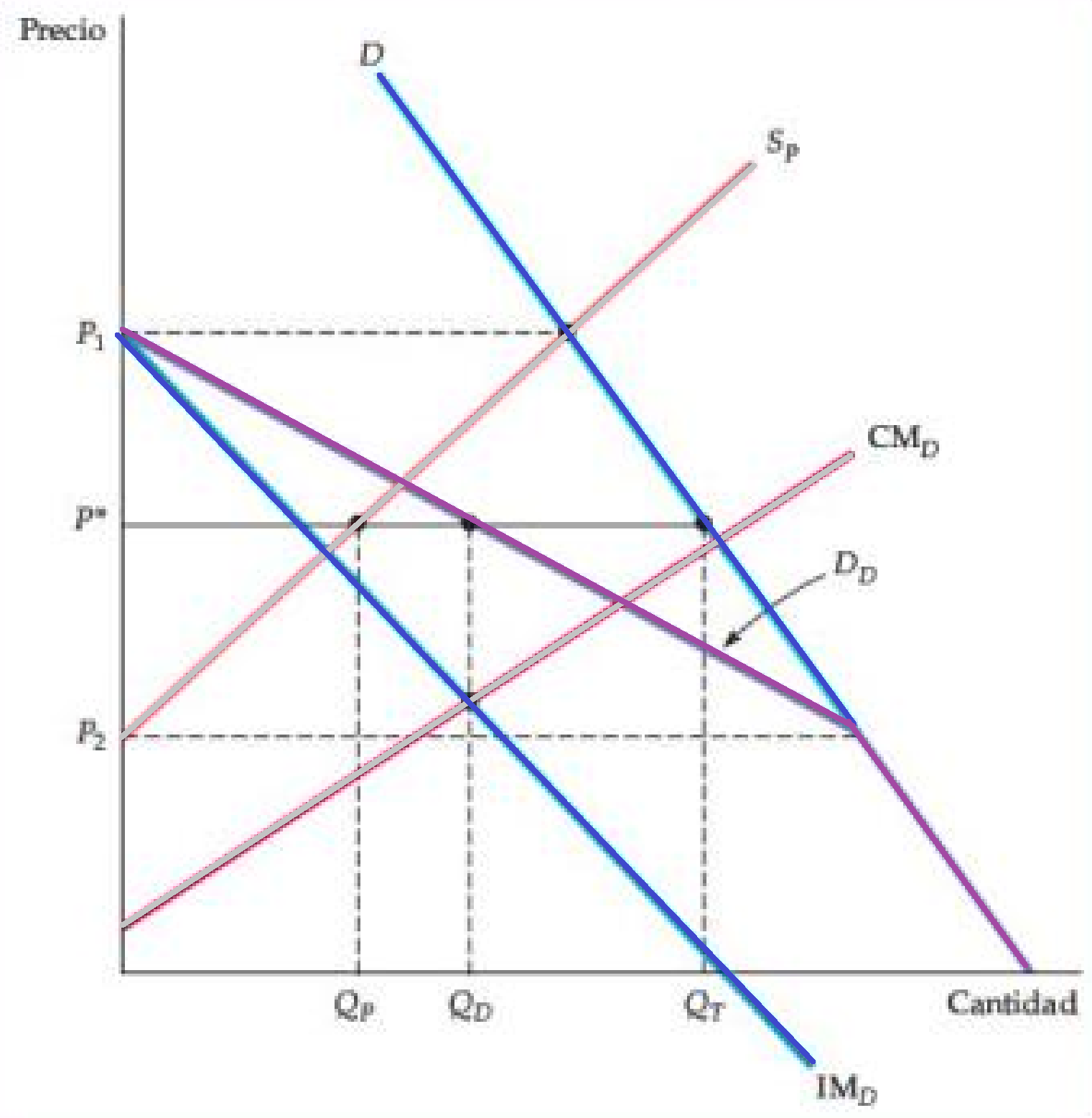
Figura: Fijación de Precios por una Empresa Dominante

• D es la curva de demanda del mercado y SF es la curva de oferta (es decir, la curva de costo marginal agregado) de las pequeñas empresas periféricas.
• La empresa dominante debe determinar su curva de demanda DD. Como muestra la figura, esta curva es simplemente la diferencia entre la demanda del mercado y la oferta de las empresas periféricas.
• Al precio P1, la oferta de las empresas periféricas es igual a la demanda del mercado; por lo tanto, la empresa dominante no puede vender nada.
• A un precio de P2 o menos, las empresas periféricas no ofrecerán ninguno de los bienes, por lo que la empresa dominante enfrenta la curva de demanda del mercado.
• A precios entre P1 y P2, la empresa dominante enfrenta la curva de demanda DD.

Implicaciones del Dilema del Prisionero

El Modelo de la Empresa Dominante (cont.)

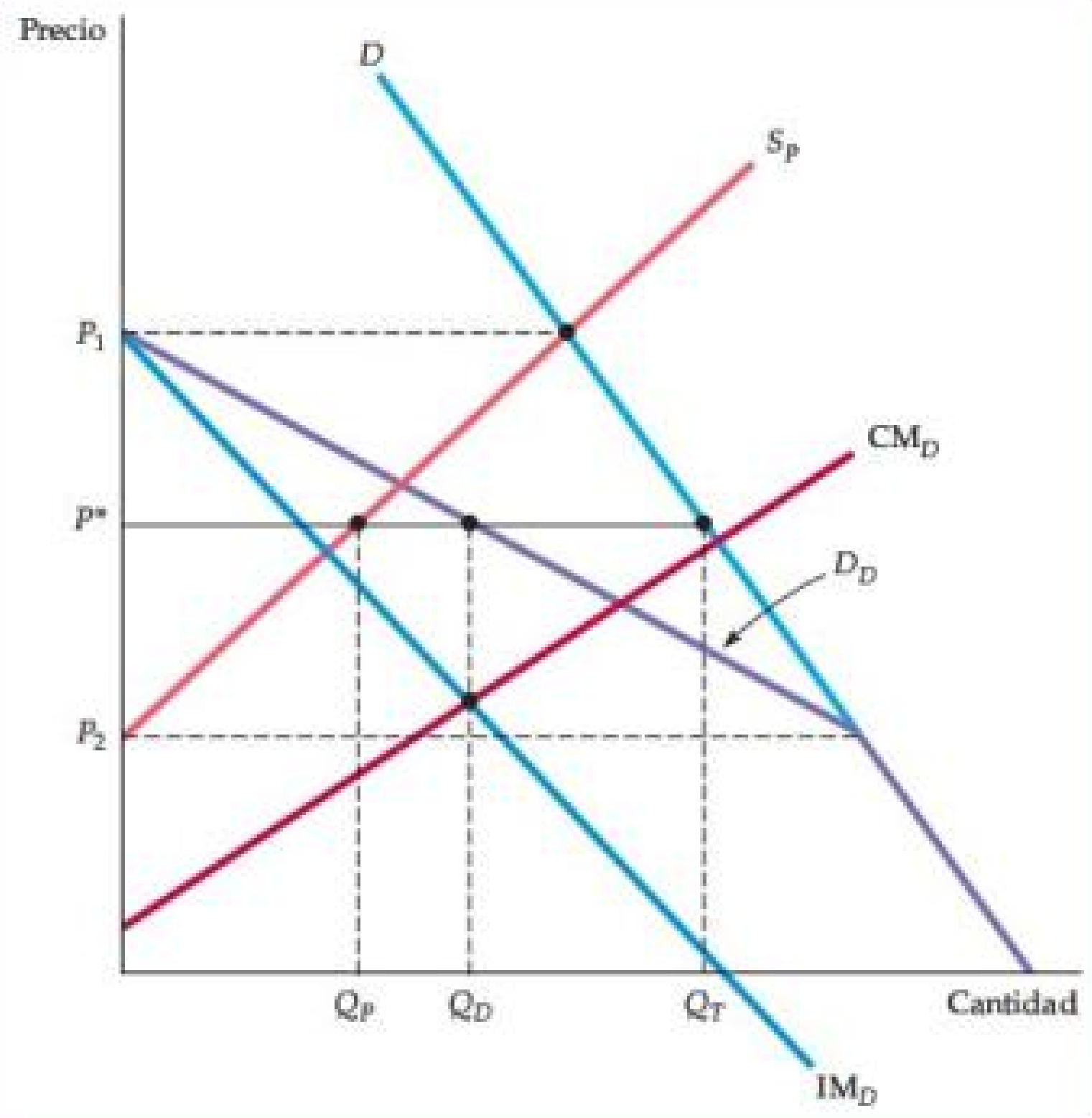
Figura: Fijación de Precios por una Empresa Dominante (continuación)

• La empresa dominante produce una cantidad QD en el punto donde su ingreso marginal MRD es igual a su costo marginal MCD.
• El precio correspondiente es P*.
• A este precio, las empresas periféricas venden QF.
• Las ventas totales son iguales a QT.

empresa dominante: Empresa con una gran cuota de ventas totales que establece el precio para maximizar sus ganancias, teniendo en cuenta la respuesta de oferta de las empresas más pequeñas.

5. Cárteles

Definición

Cártel: Mercado en el que algunas o todas las empresas coluden explícitamente, coordinando precios y niveles de producción para maximizar las ganancias conjuntas.

Cárteles

Análisis de la Fijación de Precios del Cártel. Los productores en un cártel acuerdan explícitamente cooperar en la fijación de precios y niveles de producción.

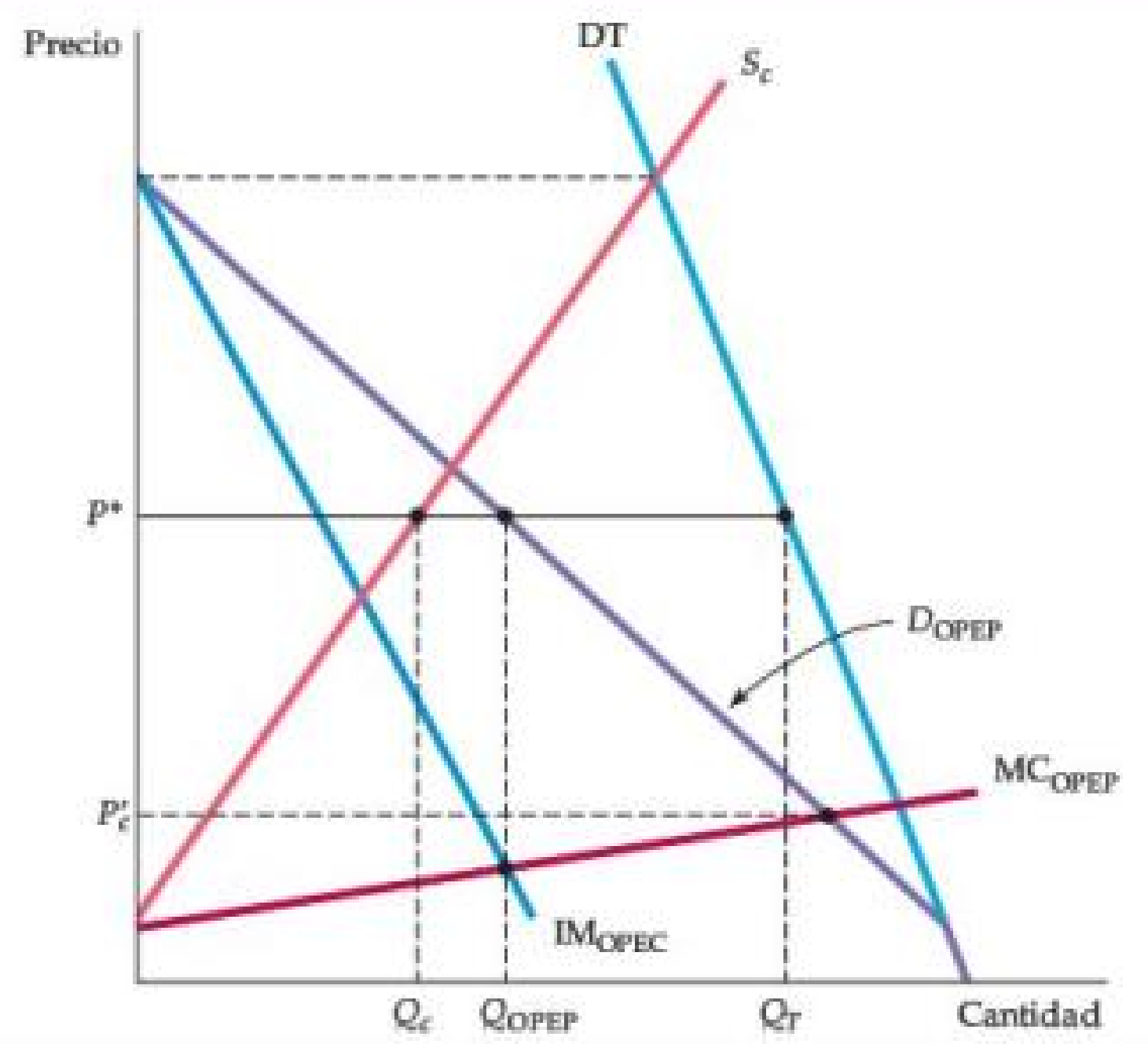
Figura: El Cártel Petrolero de la OPEP

• TD es la curva de demanda total mundial de petróleo y Sc es la curva de oferta competitiva (no OPEP).
• La demanda de la OPEP, DOPEC, es la diferencia entre las dos.
• Dado que tanto la demanda total como la oferta competitiva son inelásticas, la demanda de la OPEP es inelástica.
• La cantidad que maximiza las ganancias de la OPEP, QOPEC, se encuentra en la intersección de sus curvas de ingreso marginal y costo marginal; a esta cantidad, la OPEP cobra el precio P*.
• Si los productores de la OPEP no se hubieran cartelizado, el precio sería Pc, donde la demanda y las curvas de costo marginal de la OPEP se intersectan.

Cárteles

El Cártel de Cobre de CIPEC

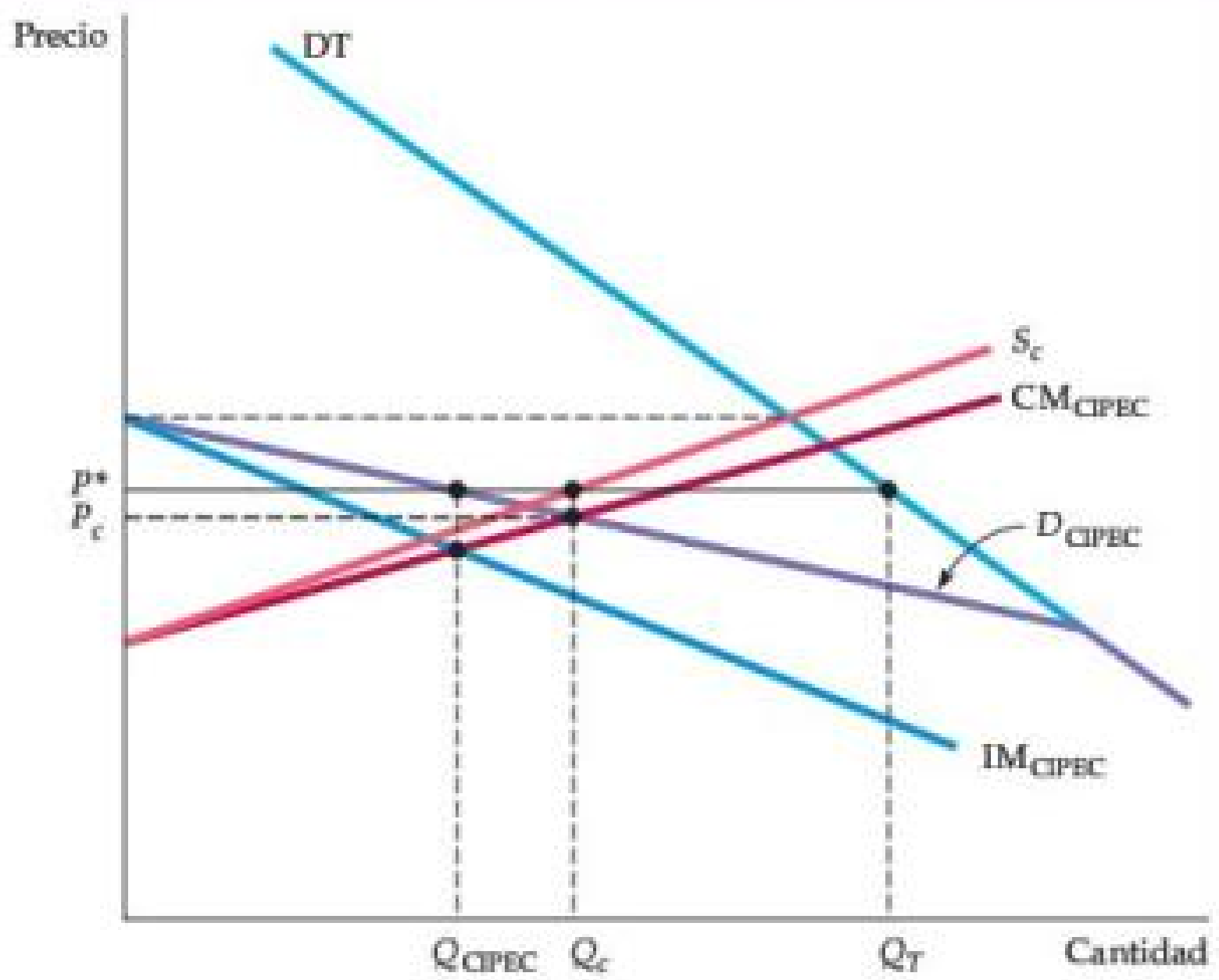
Figura: El Cártel de Cobre de CIPEC

• TD es la demanda total de cobre y Sc es la oferta competitiva (no CIPEC).
• La demanda de CIPEC, DCIPEC, es la diferencia entre las dos.
• Tanto la demanda total como la oferta competitiva son relativamente elásticas, por lo que la curva de demanda de CIPEC es elástica y CIPEC tiene muy poco poder de monopolio.
• Tener en cuenta que el precio óptimo de CIPEC, P* , está cerca del precio competitivo Pc.

Cierre

¿Preguntas?

\[\,\] O vía E-mail: luischanci@santotomas.cl