Incertidumbre

Microeconomía

Prof. Luis Chancí

Contenido

Describiendo el Riesgo
Preferencias hacia el Riesgo
Reducción del Riesgo
La Demanda de Activos Riesgosos
Economía del Comportamiento

Incertidumbre y Comportamiento del Consumidor

Para comparar el nivel de riesgo de las alternativas, necesitamos cuantificar el riesgo.

Examinaremos las preferencias de las personas hacia el riesgo.

Veremos cómo las personas pueden a veces reducir o eliminar el riesgo.

En algunas situaciones, las personas deben elegir la cantidad de riesgo que desean asumir.

En la última sección de este capítulo, ofrecemos una visión general del floreciente campo de la economía del comportamiento.

Describiendo el Riesgo

Probabilidad

probabilidad: Probabilidad de que ocurra un resultado dado.
La probabilidad subjetiva es la percepción de que un resultado ocurrirá.
valor esperado: Promedio ponderado por probabilidades de los pagos asociados con todos los resultados posibles.

Valor Esperado - pago: Valor asociado con un posible resultado. - El valor esperado mide la tendencia central: el pago o valor que esperaríamos en promedio.

Fórmula de Valor Esperado:

\[\begin{align} \text{Valor Esperado} &=& \text{Pr(éxito)}(\$40/acción) + \text{Pr(fracaso)}(\$20/acción) \\ &=& (1/4)(\$40/acción) + (3/4)(\$20/acción) \\ &=& \$25/acción \end{align}\]

\[ E(X) = \text{Pr}_1 X_1 + \text{Pr}_2 X_2 + \ldots + \text{Pr}_n X_n \]

Describiendo el Riesgo

Variabilidad

variabilidad: Grado en que los posibles resultados de un evento incierto difieren.

Ingresos de Trabajos en Ventas

Describiendo el Riesgo

Variabilidad

desviación: Diferencia entre el pago esperado y el pago real.

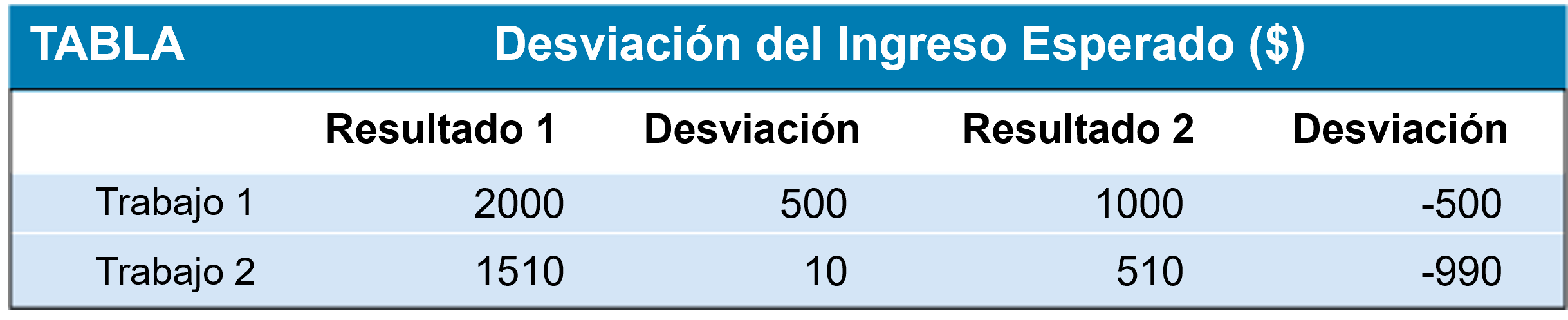
Describiendo el Riesgo

Variabilidad

La desviación al cuadrado (varianza) y la desviación estándar

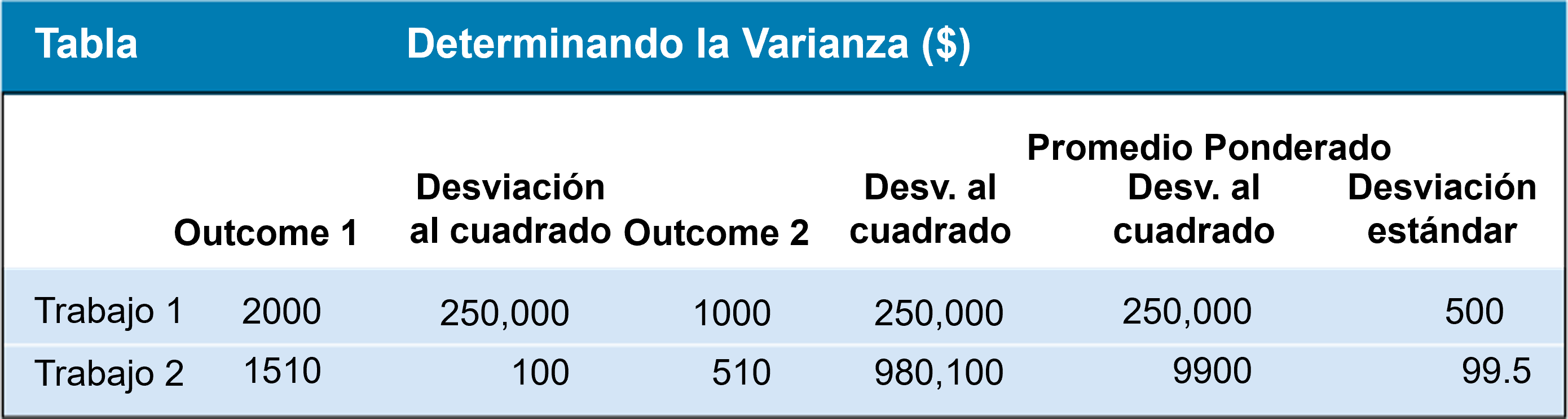
Describiendo el Riesgo

Variabilidad

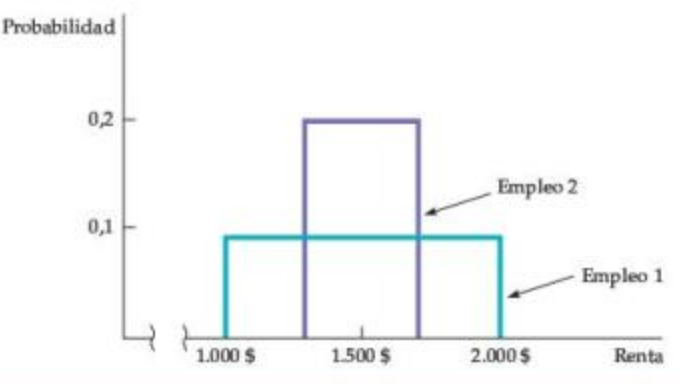
Figura: Probabilidades de resultado para dos trabajos

La distribución de pagos asociados con el Trabajo 1 tiene una mayor dispersión y una desviación estándar mayor que la distribución de pagos asociados con el Trabajo 2.

Ambas distribuciones son planas porque todos los resultados son igualmente probables.

Describiendo el Riesgo

Variabilidad

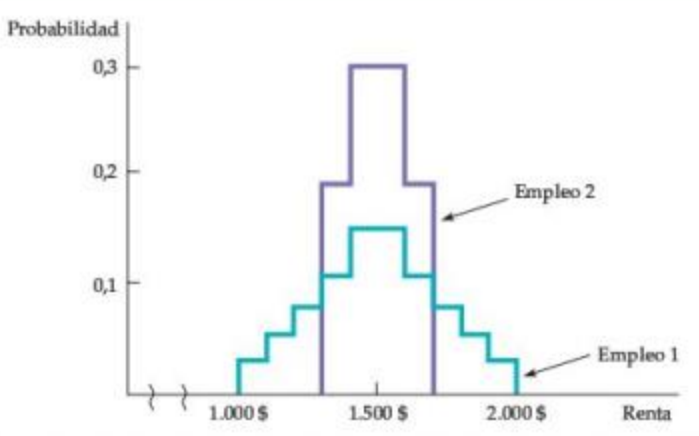
Figura: Resultados de probabilidad desigual

La distribución de pagos asociados con el Trabajo 1 tiene una mayor dispersión y una desviación estándar mayor que la distribución de pagos asociados con el Trabajo 2.

Ambas distribuciones tienen un máximo porque los resultados extremos son menos probables que los que se encuentran cerca del medio de la distribución.

Describiendo el Riesgo

Variabilidad

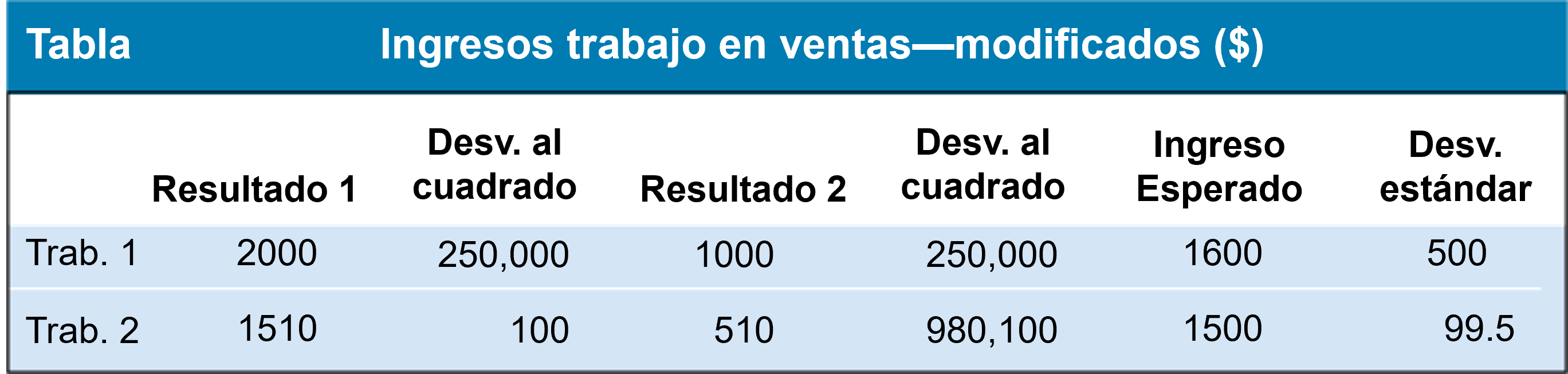
Supongamos que se aumenta el rendimiento del primer empleo en 100, por lo que los rendimientos esperados pasan a ser 1600. El cuadro muestra los nuevos ingresos y los cuadrados de las desviaciones.

Describiendo el Riesgo

Con base en los resultados de las tablas anteriores, podemos concluir que:

Dos loterías pueden tener el mismo valor esperado; sin embargo, pueden diferir en el nivel de riesgo.
El riesgo se refiere a la variabilidad de un resultado que es incierto.
Por lo tanto, un individuo adverso al riesgo preferirá, entre dos “juegos” con el mismo valor esperado, aquel que presente menor riesgo.

Preferencias bajo Incertidumbre

Utilidad Esperada

La utilidad esperada puede calcularse de forma similar al valor esperado: \[\mathbb{E}(U)=\sum_i \pi_i U_i\]

Función de Utilidad Esperada o Función de Utilidad von Neumann-Morgenstern

Para dos posibles resultados, la utilidad esperada es: \[\pi_1 \cdot U(C_1) + \pi_2 \cdot U(C_2)\]

donde $\pi$ es la probabilidad asociada a cada posible resultado y $U(C)$ es una utilidad que depende, por ejemplo, del consumo.

Preferencias (o función de utilidad) y Aversión al Riesgo

Para un individuo adverso al riesgo, se asume que la utilidad marginal de la riqueza (W) disminuye a medida que aumenta la riqueza.

Figura: Preferencias hacia el Riesgo

En la figura:

La forma de la curva representa las preferencias respecto al riesgo para el caso de un individuo adverso al riesgo.
$U(W)$ es un índice de utilidad von Neumann-Morgenstern que refleja cómo se siente el individuo respecto a cada nivel de riqueza.
La curva es cóncava para reflejar el supuesto de que la utilidad marginal es decreciente conforme aumenta la riqueza.

Preferencias y Aversión al Riesgo

Supongamos por ejemplo que $W^*$ el nivel de riqueza actual y $U(W^*)$ el nivel actual de utilidad asociado.

Supongamos que la persona enfrenta dos posibles escenarios (“juegos justos”):

Con una probabilidad de 50-50, puede perder o ganar un monto $h$. El valor esperado de la utilidad sería: \[U^h(W^*) = \frac{1}{2}U(W^* + h) + \frac{1}{2}U(W^* - h)\]
Con una probabilidad de 50-50, puede perder o ganar un monto $2h$. El valor esperado de la utilidad sería: \[U^{2h}(W^*) = \frac{1}{2}U(W^* + 2h) + \frac{1}{2}U(W^* - 2h)\]

Preferencias y Aversión al Riesgo

Gráficamente, tendríamos las siguientes situaciones:

Una persona adversa al riesgo preferirá su nivel de riqueza actual sobre la riqueza combinada en posibles escenarios inciertos (es decir, la riqueza combinada en un juego justo).

Si tuviera que enfrentar un juego, preferiría uno pequeño a uno grande.

Preferencias hacia el Riesgo

Aversion al Riesgo

Figura: Diferentes Preferencias hacia el Riesgo

En esta figura nuevamente la utilidad marginal de un consumidor disminuye a medida que aumenta el ingreso.

El consumidor es adverso al riesgo porque

preferiría un ingreso cierto de $20,000 (con una utilidad de 16)
a una apuesta con una probabilidad de 0,5 de $10,000 y una probabilidad de 0,5 de $30,000 (y una utilidad esperada de 14).

Preferencias hacia el Riesgo

Ejemplo.

Supongamos que el índice de utilidad de von Neumann-Morgenstern de una persona es logarítmico, $U(W)=Ln(W)$.

La persona posee una riqueza actual de $100 millones y enfrenta una posbilidad del 25% de perder su auto que vale $20 millones.

Determinar:

La utilidad esperada
La utilidad del valor esperado.

Preferencias hacia el Riesgo

Ejemplo (respuesta). El escenario 1 (o juego 1) es $W_1=100$ con probabilidad $\pi_1=0,75$, y el escenario 2 es $W_2=80$ con probabilidad $\pi_2=0,25$. Por ende,

La utilidad esperada es: \[\begin{eqnarray*} \mathbb{E}(U(W))&=&\pi_1\cdot U(W_1) + \pi_2\cdot U(W_2)\\ &=& 0,75*\ln(100) + 0,25*\ln(80)\\ &=& 4,5494 \end{eqnarray*}\]
La utilidad del valor esperado es: \[\begin{eqnarray*} U(\mathbb{E}(W))&=&U(\pi_1\cdot W_1 + \pi_2\cdot W_2)\\ &=& \ln(0,75*100 + 0,25*80)\\ &=& \ln(95)\\ &=& 4,5539 \end{eqnarray*}\]

Preferencias hacia el Riesgo

Diferentes preferencias respecto al riesgo

aversión al riesgo Condición de preferir un determinado ingreso a un ingreso riesgoso con el mismo valor esperado.
neutral al riesgo Condición de ser indiferente entre un ingreso determinado y un ingreso incierto con el mismo valor esperado
amante del riesgo Condición de preferir un ingreso arriesgado a un ingreso determinado con el mismo valor esperado.

Preferencias hacia el Riesgo

Aversion al Riesgo, Amante al Riego, y Neutro al Riesgo

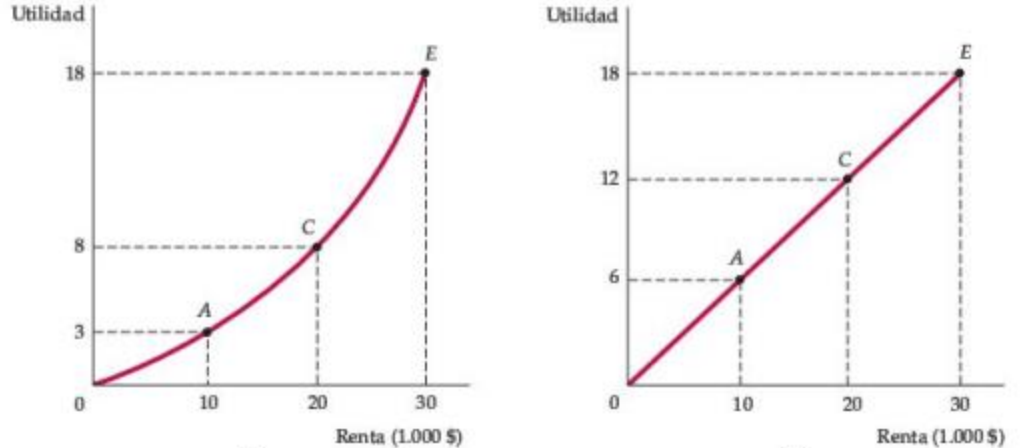
Figura: Diferentes Preferencias hacia el Riesgo

En la izquierda el consumidor es amante del riesgo: Preferiría la misma apuesta (con una utilidad esperada de 10.5) al ingreso cierto (con una utilidad de 8).

Finalmente, el consumidor en el panel derecho es neutral al riesgo e indiferente entre eventos ciertos e inciertos con el mismo ingreso esperado.

Reducción del Riesgo

El Seguro

actuarialmente justo Caracteriza una situación en la que una prima de seguro es igual al pago esperado
seguro actuarialmente justo: Caracterización de una situación en la que la prima de seguro es igual al pago esperado.

Tabla: Decisión de Asegurar (por un monto de $49000)

Seguro	Robo (Pr = 0,1)	Sin Robo (Pr = 0,9)	Ingreso Esperado	Desviación Estándar
No	40000	49000	48100	8150
Sí	49000	49000	49000	0

Ley de Grandes Numeros La capacidad de evitar riesgos operando a gran escala se basa en la ley de los grandes números, que nos dice que aunque los eventos individuales pueden ser aleatorios y en gran medida impredecibles, se puede predecir el resultado promedio de muchos eventos similares.

Reducción del Riesgo

El Valor de la Información

valor de la información completa: Diferencia entre el valor esperado de una elección cuando hay información completa y el valor esperado cuando la información es incompleta.

Tabla: Beneficios de la Venta de Trajes ($)

	Ventas de 50	Ventas de 100	Beneficio Esperado
Comprar 50 trajes	5000	5000	5000
Comprar 100 trajes	1500	12000	6750

Reducción del Riesgo

Riesgo, Prima y Seguros

El alcance de la aversión al riesgo de un individuo depende de la naturaleza del riesgo y de los ingresos de la persona. En igualdad de condiciones, las personas con aversión al riesgo prefieren una menor variabilidad de resultados.
Dado que una persona prefiere un ingreso cierto sobre uno bajo incertidumbre, puede estar dispuesta a pagar una cantidad $p$ para evitar (“participar en el juego de”) la incertidumbre.
Esto ayuda a explicar la aparición de un segundo mercado en el cual se transa el riesgo: el mercado de seguros.
Cuanto mayor sea la variabilidad del ingreso, más estaría dispuesta a pagar la persona para evitar la situación de riesgo.
Sea $p$ el monto de la prima del seguro que dejaría al individuo exactamente indiferente entre aceptar la apuesta justa de valor $h$ o pagar $p$ con certeza para evitar el riesgo:

\[\mathbb{E}(U(W + h)) = U(W - p)\]

Reducción del Riesgo

Prima de Riesgo

prima de riesgo: Cantidad máxima de dinero que una persona adversa al riesgo pagará para evitar tomar un riesgo.

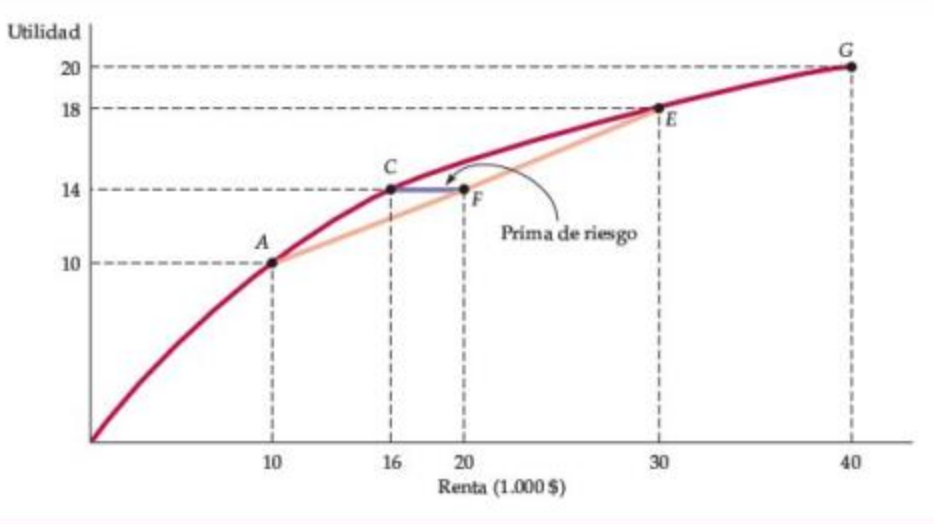
Figura: Prima de Riesgo En la figura:

La prima de riesgo CF mide la cantidad de ingreso que un individuo renunciaría para quedar indiferente entre una elección arriesgada y una cierta.
Aquí la prima de riesgo es $4000 porque un ingreso cierto de $16,000 (en el punto C) le da la misma utilidad esperada (14) que el ingreso incierto (una probabilidad de 0.5 de estar en el punto A y una probabilidad de 0.5 de estar en el punto E) que tiene un valor esperado de $20,000.

Reducción del Riesgo

Ejemplo.

Volvamos al caso en el que $U(W) = \ln(W)$, para una persona con una riqueza actual de $100$ millones y que enfrenta una probabilidad del 25% de perder su auto, cuyo valor es de $20$ millones.

Determinemos el monto de la prima de seguro justa (suponiendo que la compañía de seguros solo afronta los costos del reclamo en caso de pérdida y no incurre en costos administrativos).

Preferencias hacia el Riesgo

Ejemplo (respuesta).

Como vimos, el valor esperado de la riqueza del individuo es de $95$ millones. Así, una prima de seguro justa sería un monto equivalente al 25% de $20$ millones, es decir, alrededor de $5$ millones. Sin embargo, debido a la aversión al riesgo del individuo, el monto de la prima justa dependerá de la variabilidad asociada al riesgo. Calculamos el monto de la prima de la siguiente forma:

\[\begin{eqnarray*} \pi_1 \cdot U(W_1) + \pi_2 \cdot U(W_2) &=& U(W - p)\\ 0.75 \cdot \ln(100) + 0.25 \cdot \ln(80) &=& \ln(100 - p)\\ 4,5494 &=& \ln(100 - p)\\ e^{4,5494} &=& 100 - p\\ p &=& 100 - e^{4,5494}\\ p &\approx& 5,426 \end{eqnarray*}\]

Es decir, si $5 millones es su pérdida de riqueza esperada (bajo incertidumbre), se encuentra dispuesto a ceder a otros $0,4m extra para tener una riqueza fija o sin incertidumbre (no tener que enfrentar incertidumbre de tener 100 o 80).

Preferencias y Aversión al Riesgo

Gráficamente:

Preferencias hacia el Riesgo

Aversión al riesgo y Curvas de Indiferencia

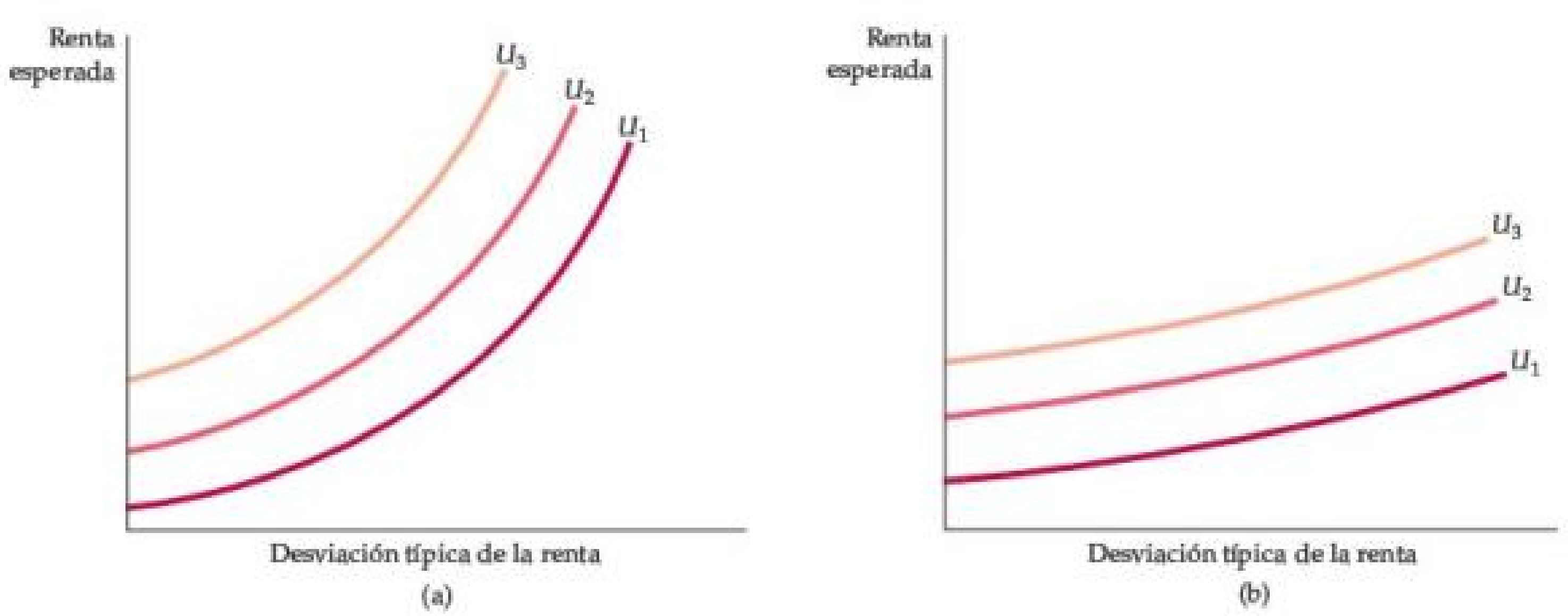
La parte (a) se aplica a una persona que tiene gran aversión al riesgo: Un aumento en la desviación estándar del ingreso de este individuo requiere un gran aumento en el ingreso esperado para que él o ella siga estando igualmente bien.

La parte (b) se aplica a una persona que tiene sólo una ligera aversión al riesgo: Un aumento en la desviación estándar del ingreso requiere sólo un pequeño aumento en el ingreso esperado para que la persona siga estando igualmente bien.

Reducción del Riesgo: Diversificación

diversificación: Práctica de reducir el riesgo asignando recursos a una variedad de actividades cuyos resultados no están estrechamente relacionados.
Variables correlacionadas negativamente Variables que tienen tendencia a moverse en direcciones opuestas.
variables correlacionadas positivamente Variables que tienen tendencia a moverse en la misma dirección.
fondo mutuo Organización que agrupa fondos de inversionistas individuales para comprar una gran cantidad de acciones u otros activos financieros diferentes.

Reducción del Riesgo: Diversificación

Ejemplo.

Un mesero debe atender distintas mesas en un restaurante, mientras más mesas atienda más propinas obtiene. Si bien las idas de la cocina a la mesa no involucran costos, existe una probabilidad de 50% (dado que todo es muy rápido en la cocina) de que los platos transportados en un viaje se le caiga uno en el trayecto. En este caso se le descuenta y no recibe propina. Esta persona piensa en dos estrategias:

Estrategia 1: llevar la bandeja con todos los platos en un viaje que le reporta una propina de $3.000 si no se cae ningún plato, si se le cae pierde la propina.
Estrategia 2: hacer dos viajes y llevar un equivalente a propina de $1.500 en cada uno de ellos.

Realizar una lista de los posibles resultados de cada estrategia y de las probabilidades de estos resultados.
Obtener el valor esperado en cada estrategia.
Determinar la utilidad esperada si la función de utilidad es $U(W) = W^{1/2}$. ¿Qué estrategia elegiría el mesero?

Reducción del Riesgo: Diversificación

Ejemplo (respuesta).

a. Lista de los posibles resultados y probabilidades.

Estrategia 1:

	Se cae (prob 50%)	No se cae (prob 50%)
Propina ($)	0	3000

Estrategia 2:

\[ \begin{array}{cc|ll} & & \text{Viaje 2}&\\ & & \text{Se cae} & \text{No se cae} \\ \hline \text{Viaje 1} & \text{Se cae} & 0 & 1500\\ & \text{No se cae} & 1500 & 3000\\ \end{array} \]

Reducción del Riesgo: Diversificación

Ejemplo (respuesta).

b. Obtenga el valor esperado en cada estrategia.

Estrategia 1:

\[Valor\,Esperado\, = 0.5*3000 + 0.5*0 = 1500\]

Estrategia 2:

\[Valor\,Esperado\, = 0.25*0 + 0.25*1500 + 0.25*1500 + 0.25*3000 = 1500\]

Reducción del Riesgo: Diversificación

Ejemplo (respuesta).

c. Determinar la utilidad esperada. ¿Qué estrategia elegiría el mesero?

Estrategia 1:

\[\mathbb{E}(U) = 0,5*(3000)^{1/2} + 0,5*(0)^{1/2} = 27,38\]

Estrategia 2:

\[\mathbb{E}(U) = 0,25*(0)^{1/2} + 0,25*(1500)^{1/2} + 0,25*(1500)^{1/2} + 0,25*(3000)^{1/2} = 33,05\]

Conclusión: Elegiría, dadas sus preferencias, la estrategia 2, porque su utilidad esperada es mayor.

La Demanda de Activos Riesgosos

Activo

activo: Algo que proporciona un flujo de dinero o servicios a su propietario.

Un aumento en el valor de un activo es una ganancia de capital; una disminución es una pérdida de capital.
activo sin riesgo (o libre de riesgo): Activo que proporciona un flujo de dinero o servicios que se conoce con certeza.

Ejemplo: Bonos del gobierno como el ‘U.S. Treasury Bonds’. El retorno es predecible.
activo riesgoso: Activo que proporciona un flujo incierto de dinero o servicios a su propietario.

Ejemplo: Acciones de una empresa. Al adquirir acciones de Apple en la bolsa de valores, el monto a recuperar en unos años dependerá de muchos factores, tales como el desempeño de la empresa o condiciones macroeconómicas.

La Demanda de Activos Riesgosos

Rendimientos de los Activos:

rendimiento: Flujo monetario total de un activo como una fracción de su precio.
rendimiento real: Rendimiento simple (o nominal) de un activo, menos la tasa de inflación.

Rendimientos Esperados versus Reales:

rendimiento esperado: Rendimiento que un activo debería obtener en promedio.
rendimiento real: Rendimiento que un activo obtiene.

TABLA: Inversiones—Riesgo y Rendimiento (1926–2006)

	Tasa Promedio de Rendimiento (%)	Tasa Real Promedio de Rendimiento (%)	Riesgo de Tasa (Desviación Estándar, %)
Acciones comunes (S&P 500)	12.3	9.2	20.1
Bonos corporativos a largo plazo	6.2	3.1	8.5
Letras del Tesoro de EE.UU.	3.8	0.7	3.1

La Demanda de Activos Riesgosos

La Compensación (disyuntiva) entre Riesgo y Rendimiento

La Cartera de Inversión

\[ R_p = bR_m + (1 - b)R_f \]
\[ \sigma_p = b\sigma_m \]

El Problema de Elección del Inversionista

\[ R_p = R_f + b(R_m - R_f) \] \[ R_p = R_f + \left(\frac{R_m - R_f}{\sigma_m}\right)\sigma_p \]

Precio del riesgo: Riesgo adicional que un inversor debe asumir para disfrutar de un mayor rendimiento esperado.

La Demanda de Activos Riesgosos

El Problema de Elección del Inversionista

Riesgo y Curvas de Indiferencia

Elegir entre Riesgo y Rendimiento

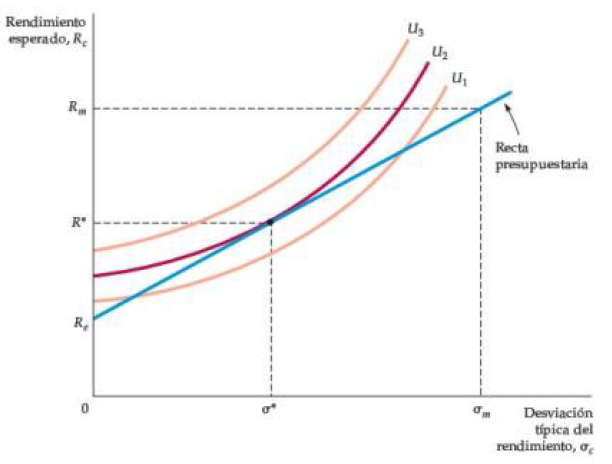
Un inversionista está dividiendo sus fondos entre dos activos: Letras del Tesoro, que son libres de riesgo, y acciones. La línea de presupuesto describe la compensación entre el rendimiento esperado y su nivel de riesgo, medido por la desviación estándar del rendimiento.

La pendiente de la línea de presupuesto es $(R_m - R_f)/\sigma_m$ , que es el precio del riesgo.

Se dibujan tres curvas de indiferencia, cada una mostrando combinaciones de riesgo y rendimiento que dejan al inversionista igualmente satisfecho.

Las curvas son ascendentes porque un inversionista adverso al riesgo requerirá un mayor rendimiento esperado si debe asumir un mayor riesgo. La cartera de inversión que maximiza la utilidad está en el punto donde la curva de indiferencia $U_2$ es tangente a la línea de presupuesto.

La Demanda de Activos Riesgosos

El Problema de Elección del Inversionista

Riesgo y Curvas de Indiferencia

Las Elecciones de Dos Inversionistas Diferentes

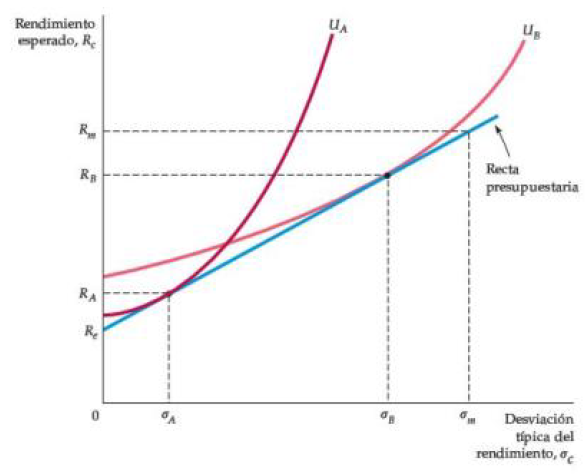
El inversionista A es altamente adverso al riesgo. Debido a que su cartera consistirá principalmente en el activo sin riesgo, su rendimiento esperado $R_A$ será solo ligeramente mayor que el rendimiento sin riesgo. Sin embargo, su riesgo $\sigma_A$ será pequeño.

El inversionista B es menos adverso al riesgo. Ella invertirá una gran fracción de sus fondos en acciones. Aunque el rendimiento esperado de su cartera $R_B$ será mayor, también será más riesgoso.

La Demanda de Activos Riesgosos

El Problema de Elección del Inversionista

Riesgo y Curvas de Indiferencia

Comprar Acciones en el Margen (crédito)

Debido a que el inversionista A es adverso al riesgo, su cartera contiene una mezcla de acciones y letras del Tesoro libres de riesgo.

El inversionista B, sin embargo, tiene un muy bajo grado de aversión al riesgo. Su curva de indiferencia, (U_B), es tangente a la línea de presupuesto en un punto donde el rendimiento esperado y la desviación estándar de su cartera exceden los del mercado de acciones en general.

Esto implica que le gustaría invertir más del 100 por ciento de su riqueza en el mercado de acciones. Lo hace comprando acciones a crédito, es decir, tomando prestado de una firma de corretaje para ayudar a financiar su inversión.

Economía del Comportamiento

Recordemos que la teoría básica de la demanda del consumidor se basa en tres suposiciones:

Los consumidores tienen preferencias claras por algunos bienes sobre otros;
Los consumidores enfrentan restricciones presupuestarias; y
Dados sus preferencias, ingresos limitados y los precios de diferentes bienes, los consumidores eligen comprar combinaciones de bienes que maximicen su satisfacción o utilidad.

Sin embargo, estas suposiciones no siempre son realistas.

Quizás nuestra comprensión de la demanda del consumidor (así como las decisiones de las empresas) mejoraría si incorporáramos suposiciones más realistas y detalladas sobre el comportamiento humano.

Este ha sido el objetivo del campo floreciente de la economía del comportamiento.

Economía del Comportamiento

Algunos ejemplos de comportamiento del consumidor que no pueden ser fácilmente explicados con las suposiciones básicas de maximización de utilidad:

Ha habido una gran tormenta de nieve, por lo que te detienes en la ferretería para comprar una pala de nieve. Esperabas pagar $20 por la pala, el precio que la tienda normalmente cobra. Sin embargo, encuentras que la tienda ha subido repentinamente el precio a $40. Aunque esperarías un aumento de precio debido a la tormenta, sientes que un doble del precio es injusto y que la tienda está tratando de aprovecharse de ti. Por despecho, no compras la pala.
Cansado de estar atrapado en casa por la nieve, decides tomar unas vacaciones en el campo. En el camino, te detienes en un restaurante de carretera para almorzar. Aunque es poco probable que vuelvas a ese restaurante, crees que es justo y apropiado dejar una propina del 15% en agradecimiento por el buen servicio que recibiste.
Compras este libro de texto en un librero de Internet porque el precio es más bajo que en tu librería local. Sin embargo, ignoras el costo de envío al comparar precios.

Economía del Comportamiento

Preferencias Más Complejas

punto de referencia: El punto desde el cual un individuo toma una decisión de consumo.
efecto dotación: Tendencia de los individuos a valorar un artículo más cuando lo poseen que cuando no lo poseen.
aversión a la pérdida: Tendencia de los individuos a preferir evitar pérdidas en lugar de adquirir ganancias.

Reglas Empíricas y Sesgos en la Toma de Decisiones

anclaje: Tendencia a confiar en gran medida en una pieza de información previa (sugerida) al tomar una decisión.

Economía del Comportamiento

Probabilidades e Incertidumbre

Una parte importante de la toma de decisiones bajo incertidumbre es el cálculo de la utilidad esperada, que requiere dos piezas de información: un valor de utilidad para cada resultado (de la función de utilidad) y la probabilidad de cada resultado.

Las personas a veces son propensas a un sesgo llamado la ley de los pequeños números: tienden a exagerar la probabilidad de que ciertos eventos ocurran cuando se enfrentan a relativamente poca información de la memoria reciente.

Formar probabilidades subjetivas no siempre es una tarea fácil y las personas generalmente son propensas a varios sesgos en el proceso.

Resumiendo

La teoría básica que hemos aprendido hasta ahora nos ayuda a entender y evaluar las características de la demanda del consumidor y a predecir el impacto en la demanda de los cambios en los precios o ingresos.

El campo en desarrollo de la economía del comportamiento intenta explicar y elaborar aquellas situaciones que no están bien explicadas por el modelo básico del consumidor.

Cierre

¿Preguntas?